Учебное пособие 1305

При делении комплексных чисел z1 и z2, заданных в тригонометрической форме, модули комплексных чисел делятся, а аргументы вычитаются. По определению:

Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя.

В показательном представлении операции с модулями и аргументами комплексных чисел при делении совпадают с таковыми при делении в тригонометрическом виде:

z1 = r1 ei(ϕ1 −ϕ2 ). z2 r2

Возведение комплексного числа в целую положительную степень является распространением правила умножения комплексных чисел на случай, когда все n множителей одинаковы. В алгебраическом представлении возведение комплексного числа в n -ую степень производится по алгебраическим правилам перемножения многочленов с учетом того, что

i2 = −1, i3 = i2i = −i, i4 = i3i =1.

80

В тригонометрическом представлении модуль n -ой степени комплексного числа равен n - ой степени модуля исходного комплексного числа, а аргумент n -ой степени комплексного числа получается посредством умножения на n аргумента исходного комплексного числа. В итоге получается формула Муавра:

zn = r n (cos nϕ +i sin nϕ).

В показательном представлении имеем: zn = r neinϕ .

Пример 4.3.5. Вычислить (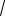3 +i)12 .

Решение: Запишем число z = 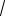3 +i в тригонометриче-

Произведя по указанным правилам возведение в двенадцатую степень комплексного числа, имеем

Извлечение корня n - степени определяется как действие, обратное возведению в натуральную степень. Корнем n-ой степени из комплексного числа z называется такое комплекс-

ное число w , что выполняется равенство wn = z .

Если комплексные числа z и w представлены в тригонометрической форме

z = r(cosϕ +i sinϕ) и w = ρ(cosθ +i sinθ),

то, по определению корня и формуле Муавра, получаем z = wn = ρn (cos nθ +i sin nθ)= r(cosϕ +i sinϕ).

Согласно определению два комплексных числа равны, если равны их модули, а аргументы равны или отличаются на

81

четное число π , поэтому ρn = r или ρ = nr , а nθ =ϕ + 2kπ ,

k = 0,±1,±2,... или θ = ϕ + 2kπ . n

Тогда, определению корня n −ой степени из комплексного числа удовлетворяют n комплексных чисел, описываемых формулой

Операция извлечения корней n −ой степени из комплексного числа оказывается многозначной, т.е. n значениям параметра k (k = 0,1,2,..., n −1) соответствуют n различных значе-

ний аргумента θk , а поэтомуи n значений самого корня n −ой

степени из комплексного числа. Остальным целым k соответствуют значения θk , отличающиеся от одного из указанных

значений на величину, кратную 2π и не дающие новых значений корня.

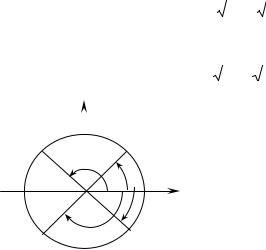
Таким образом, комплексное число z ≠ 0 имеет ровно n корней степени n, получаемых из вышеприведенной формулы. Следует отметить, что все значения корня лежат на окружно-

сти радиуса ρ= nr и делят окружность на n равных частей.

Рис. 18

Вопросы для самопроверки

1.Дайте определение комплексного числа.

2.Где на комплексной плоскости изображаются мнимые

числа?

3.Что собой представляет алгебраическая форма записи комплексного числа?

4.Какие комплексные числа называются равными?

5.Относительно какой оси комплексно-сопряженные числа располагаются симметричным образом?

6.Как называется длина радиус-вектора, соответствующего комплексному числу?

7.Что является аргументом комплексного числа?

8. Как вычисляется аргумент комплексного числа, представленного в алгебраическом виде, расположенного в третьей четверти?

83

9. Как производится сложение комплексных чисел в алгебраическом представлении?

10. Какими свойствами обладает операция сложения комплексных чисел?

11. Что происходит с аргументами и модулями комплексных чисел при сложении?

12. Дайте определение натуральной степени комплексного числа.

13. Как определяется модуль корня n − степени комплексного числа?

Задачи для самостоятельного решения

3.(1+i)6 (Ответ: −8i ).

4.61 (Ответ: cos k3π +i sin k3π (k = 0,1,2,3,4,5)).

5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

5.1. Основные понятия

Часто при рассмотрении различных прикладных задач построение математических моделей приводит к уравнениям, связывающим независимую переменную x , искомую фун к-

цию y = y(x) и производные функции различных порядков.

Такие уравнения называются дифференциальными. Решением или интегралом дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Если неизвестная функция y = y(x) зависит от одной

переменной, то дифференциальное уравнение называетсяобыкновенным. Дифференциальные уравнения в частных производных, соответствующие случаю зависимости искомой функции от нескольких переменных, в данном курсе не рассматриваются. Далее будем рассматривать только обыкновенные дифференциальные уравнения.

Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения. Например, уравнение y′′−3y′+ 2y = 0 является обыкновенным

дифференциальным уравнением второго порядка, а уравнение y′+ 5xy = y2 - первого порядка.

Нахождение решения дифференциального уравнения называется его интегрированием, а график решения дифференциального уравнения представляется интегральной кривой.

5.2 Дифференциальные уравнения первого порядка. Основные понятия

Дифференциальное уравнение первого порядка, связывающее независимую переменную х, искомую функцию y(x) и ее

85

производную у' в общем случае можно записать в виде

F(x; y; y′)= 0 .

Дифференциальное уравнение первого порядка, разрешенное относительно у', записывается в виде y′ = f (x; y).

Дифференциальное уравнение первого порядка может

функции.

Существует бесчисленное множество решений дифференциального уравнения, отличающихся друг от друга на постоян-

уравнения первого порядка составляет понятие общего решения дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка называется функция y =ϕ(x;c), содержащая одну про-

извольную постоянную c , обращающая для любого фиксированного значения c дифференциальное уравнение в тождество, причем, любое частное решение из вышеупомянутой совокупности решений может быть получено из общего решения при некотором конкретном значении c .

Частным решением дифференциального уравнения пер-

вого порядка называется любая функция y =ϕ(x;c0 ), полученная из общего решения y =ϕ(x;c) при конкретном значении по-

стоянной c = c0 .

Часто общее решение дифференциального уравнения может быть получено только в неявном виде, т. е. в виде уравнения

Ф(x; y;c)= 0 , которое называется общим интегралом дифференциального уравнения.

86

С геометрической точки зрения общее решение y =ϕ(x;c) представляет собой семейство интегральных кривых на плоскости Oxy . Частное решение y = ϕ(x;c0 ) соответствует одной

кривая из этого семейства. Для выделения конкретной кривой используется точка (x0 ; y0 ), принадлежащая кривой. В этом

случае говорят о начальном условии y0 =ϕ(x0 ), которому

удовлетворяет данное частное решение. Задача отыскания частного решения дифференциального уравнения первого порядка, удовлетворяющего заданному начальному условию, называет-

ся задачей Коши.

Интегральная кривая, проходящая через точку (x0 , y0 ), единственна.

5.3. Уравнения сразделяющимися переменными

Наиболее простым дифференциальным уравнением первого порядка является уравнение вида

P(x) dx +Q(y) dy = 0 ,

где каждая из функций P(x) и Q(y) зависит только отодной пе-

ременной. Такие дифференциальные уравнения называют уравнениями с разделенными переменными. Проинтегрировав по-

членно это уравнение, получаем: ∫P(x) dx + ∫Q(y) dy = c - его

общий интеграл.

Дифференциальные уравнения с разделяющимися пере-

менными имеют вид P1 (x)Q1 (y)dx + P2 (x)Q2 (y)dy = 0 .

Уравнение легко сводится к предыдущему уравнению путем почленного деления его на Q1 (y)P2 (x), после чего может

При проведении почленного деления дифференциального

87

уравнения на Q1 (y)P2 (x) могут быть потеряны некоторые реше-

уравнения, которые не принадлежат семействуобщего решения. Пример 5.3.1. Найти общее решение дифференциального

уравнения dydx = − xy .

Решение: Разделим переменные dyy = − dxx . Интегрируя, находим ∫ dyy = −∫ dxx +C, т.е.

ln y = −ln x + ln C или ln y = ln C / x отсюда получаем общее

решение: у = С/x.

Пример 5.3.2. Найти общий интеграл дифференциального уравнения (y + xy)dx + (x − xy)dy = 0 .

Решение: Преобразуем левую часть уравнения: y(1+ x)dx + x(1− y)dy = 0.

Делим обе части уравнения на xy ≠ 0 : 1+x x dx + 1−y y dy = 0.

Решением его является общий интеграл x + ln x + ln y − y = c ,

т.е. ln xy + x − y = c .

Здесь уравнение Q1 (y)P2 (x)= 0 имеет вид xy = 0. Его решения x = 0 , y = 0 являются решениями данного дифференци-

ального уравнения, но не входят в общий интеграл. Значит, решения x = 0, y = 0 являются особыми.

Уравнение y′ = f1 (x)f2 (y) также сводится к уравнению с разделенными переменными. Для этого достаточно положить

y′ = dydx и разделитьпеременные.

88

5.4. Однородные уравнения первого порядка

Функция f (x, y) называется однородной функцией n-го порядка относительно переменных х и у, если при любом λ справедливо тождество f (λx,λy)= λn f (x, y).

однородным, если функция f (x; y) есть однородная функция

нулевого порядка.

Покажем, что однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными. Если

f (x; y) - однородная функция нулевого порядка, то, по опре-

рядка зависит только от отношения xy . Поэтому сделаем под-

становкуu = xy , т.е. y = ux . Дифференцирование последнего

равенства дает dydx = u + dudx x . Подставляя производную в урав-

нение, получим дифференциальное уравнение с разделяющимися переменными

Интегрируя, находим

∫ f (1,duu)−u = ∫dxx +C. 89