
Учебное пособие 800318
.pdfсоответствующий интервал. Таким образом, значения, представленные в графах 3 и 4 таблицы 10.1, дают экспериментальное статистическое распределение случайной величины в численной форме. В графической форме это распределение показано на рис. 6.2 (пунктирная кривая).
Рассмотрим гипотезу о соответствии экспериментального закона распределения, представленного статистическим рядом в численной форме, а в графической форме на рис. 6.2 (пунктирная кривая), теоретическому (гауссовскому) закону распределения. Для этого используем критерий Пирсона.
Вкачестве теоретического (гауссовского) закона распределения используем распределение, представленное в численной форме в графах 3 и 5 табл. 10.1 а в графической форме на рис. 8.2 (сплошная кривая). Теоретический ряд, также как и экспериментальный статистический ряд разбиваем на 19 интервалов (табл. 10.1 и рис. 10.1).
Как указывалось выше, предпосылкой применения критерия Пирсона является достаточная заполненность интервалов частотами, т.е. на практике рекомендуется иметь в каждом интервале не менее 5-10 наблюдений. Если число наблюдений в отдельных интервалах мало, то имеет смысл объединить эти интервалы. Если необходимо объединять какое-то количество интервалов экспериментального ряда, то аналогичные интервалы теоретического ряда тоже объединяются и наоборот.
Внашем случае, чтобы экспериментальные частоты получились не менее 5, необходимо сделать объединение первых четырех интервалов с номерами 1, 2, 3 и 4: (1+2+5+13)=21/4=5,25, что более 5; аналогично, делаем объединение первых четырех интервалов теоретического ряда: (2+4+8+18)=32/4=8.что тоже более 5, это означает, что объединение первых четырех интервалов достаточно.
41
Таблица 10.1 Интервальный ряд случайных величин для экспериментального
(графы 3 и 4) и теоретического (графы 3 и 5) законов распределения (до объединения
интервалов)
Номе |
|
Середи |
Частота m'i |
Частота |
|
р |
Границы |
mi |
|||
инте |
интервалов |
на |
эксперимента |
теорети |
|
интерва |
|||||
рвал |
(классов) |
льного ряда |
ческого |
||
а |
|
ла |
|
ряда |
|
|
|
|
|||
1 |
190,5-191,5 |
191 |
1 |
2 |
|
2 |
191,5-192,5 |
192 |
2 |
4 |
|
3 |
192,5-193,5 |
193 |
5 |
8 |
|
4 |
193,5-194,5 |
194 |
13 |
18 |
|
5 |
194,5-195,5 |
195 |
30 |
35 |
|
6 |
195,5-196,5 |
196 |
60 |
60 |
|
7 |
196,5-197,5 |
197 |
90 |
85 |
|
8 |
197,5-198,5 |
198 |
97 |
95 |
|
9 |
198,5-199,5 |
199 |
98 |
99 |
|
10 |
199,5-200,5 |
200 |
100 |
100 |
|
11 |
200,5-201,5 |
201 |
98 |
99 |
|
12 |
201,5-202,5 |
202 |
97 |
95 |
|
13 |
202,5-203,5 |
203 |
90 |
85 |
|
14 |
203,5-204,5 |
204 |
60 |
60 |
|
15 |
204,5-205,5 |
205 |
25 |
35 |
|
16 |
205,5-206,5 |
206 |
10 |
18 |
|
17 |
206,5-207,5 |
207 |
3 |
8 |
|
18 |
207,5-208,5 |
208 |
2 |
4 |
|
19 |
208,5-209,5 |
209 |
1 |
2 |
42
Проверим необходимость объединения последних интервалов экспериментального и теоретического рядов. Для экспериментального ряда попробуем объединить четыре последних интервала с номерами 16, 17, 18 и19, вычислим: (10+3+2+1)=16/4=4, т.е. величина менее 5, значит надо объединять последние пять интервалов с номерами 15, 16, 17, 18 и 19 . Вычисления дают: для экспериментального ряда: (25+10+3+2+1)=41/5=8,2, т.е. величина более 5, а для теоретического ряда: (35+18+8+4+2)/5=67/5=13,4, т.е.
величина также более 5. Значит, объединение последних пяти интервалов достаточно.
Таблица 10.2 Интервальный ряд случайных величин для экспериментального
(графы 3 и 4) и теоретического (графы 3 и 5) законов распределения (после объединения интервалов).
|
|
|
Час |
|
|
|
|
|
|
|
тот |
|
|
|
|
|
Границы |
|
а |
|
|
|
|
|
Сер |
экс |
Част |
|
|
|
|
|
интервал |
|
2 |
|
|||
|
ов после |
еди |
пер |
ота |
i |
) |
mi, mi 2 |
|
на |
име |
теорети |
m- |
i |
||
|
объедине |
инт |
нта |
ческого |
i |
i –m |
|
|
ния |
ерв |
льн |
ряда |
m’ |
(m’ |
mi |
|
интервал |
ала |
ого |
mi |
|
|
|
|
ов |
|
ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а, |
|
|
|
|
|
|
|
m'i |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
1 |
190,5- |
192, |
5,25 |
8 |
2, |
7,6 |
0,95 |
|
194,5 |
5 |
|
|
75 |
|
|
2 |
194,5- |
195 |
30 |
35 |
5 |
25 |
0,71 |
|
195,5 |
|
|
|
|
|
|
3 |
195,5- |
196 |
60 |
60 |
0 |
0 |
0 |
|
196,5 |
|
|
|
|
|
|
43
Продолжение табл. 10.2
4 |
196,5- |
197 |
90 |
85 |
5 |
25 |
0,3 |
|
197,5 |
|
|
|
|
|
|
5 |
197,5- |
198 |
97 |
95 |
2 |
4 |
0,04 |
|
198,5 |
|
|
|
|
|
|
6 |
198,5- |
199 |
98 |
99 |
1 |
1 |
0,01 |
|
199,5 |
|
|
|
|
|
|
7 |
199,5- |
200 |
100 |
100 |
0 |
0 |
0,00 |
|
200,5 |
|
|
|
|
|
|
8 |
200,5- |
201 |
98 |
99 |
1 |
1 |
0,01 |
|
201,5 |
|
|
|
|
|
|
9 |
201,5- |
202 |
97 |
95 |
2 |
4 |
0,04 |
|
202,5 |
|
|
|
|
|
|
10 |
202,5- |
203 |
90 |
85 |
5 |
25 |
0,3 |
|
203,5 |
|
|
|
|
|
|
11 |
203,5- |
204 |
60 |
60 |
0 |
0 |
0 |
|
204,5 |
|
|
|
|
|
|
12 |
204,5- |
207 |
8,2 |
13,4 |
5, |
27 |
2,02 |
|
209,5 |
|
|
|
2 |
|
|
|
|
Сумма |
|
|
|
4,4 |
|
|
|
|
|
|
|
|
|
44
120 |
mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
m m10m11 |
|
|
|
|
||
|
|
|
m' |
|
m'12 |
|
|
|
||
|
|
|
m' |
m |
m'm'10m'1 |
m'1 |
|
|
|
|
|
|
|
|
m12 |
|
|
|
|||
|
|
|
m |
|
|
m1 |
|
|
|
|
80 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
60 |
|
m' |
m |
|
|
|
m'1 m1 |
|
|
|
40 |
|
m |
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
m' |
|
|
|
|
|
|
|
|
20 |
|
m |
|
|
|
|
m'1 |
m1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
m |
m' |
|
|
|
|
|
|
m1 |
|
m m |
|
|
|
|
|
|
m'1 |
m1m1 |
||
0 |
m' m' |
|
|
|
|
|
m'1 |
m'1 m'1 |
||
|
m' |
|
|
|
|
|
|
|
||
191 |
193 |
195 |
197 |
199 |
201 |
203 |
205 |
207 |
209 |
x |
|
||||||||||
|
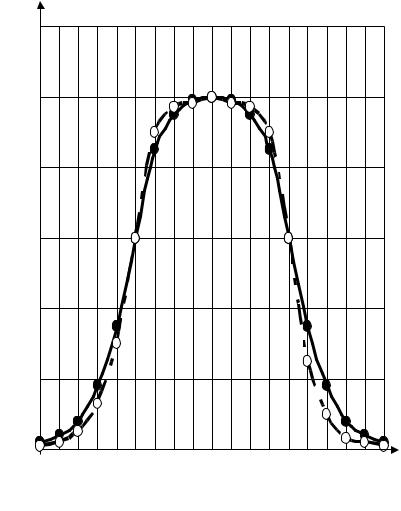
Рис. 10.1. Графики распределения случайных |
|
||||||||
величин для экспериментального (пунктирная линия) |
||||||||||
и теоретического (сплошная линия) законов распределения (до |
||||||||||
|
|
объединения интервалов) |
|
|
|
|||||
45

Таким образом, после объединения число интервалов станет равным 19-3-4=12. Значения экспериментальных и теоретических частот после объединения интервалов приведены в табл. 10.2 : в графах 3 и 4 для экспериментального распределения, а в графах 3 и 5- для теоретического распределения случайных величин. В табл. 10.2 приведены также значения разностей экспериментальных и теоретических частот для каждого интервала (графа 6), значения их квадратов (графа 7) и значения отношений квадрата разности к соответствующей частоте теоретического ряда (графа 8).
Подставив значения m1 и тi в выражение (2.23), получим
(mi mi ) = 0,95+0,71+0,0+0,3+0,04+ +0,01+
i1 mik ' 2
0,0+0,01+0,04+0,3+0,0+2,02= 4,37
Число степеней свободы в соответствии с (2.24) равно
ν = k – f =12 - 3 = 9
По табл. П1 для χ 2 = 4,37 и ν = 9 находим, что Р = 0,9. Следовательно, экспериментальное распределение значений напряжения, приведенное в табл. 10.2 и показанное на рис. 10.1 близко к гауссовскому, что означает отлаженность и стабильность технологического процесса производства.
46
ЛЕКЦИЯ 5
11. Cемь инструментов статистического контроля качества
Для эффективного обеспечения контроля качества необходимо участие и сотрудничество всех без исключения работников предприятия от рабочего до руководителя. Реализуемый таким образом контроль качества стал называться всеобщим контролем качества [Total Quality Control (TQC)]. С
целью обучения персонала статистическим методам контроля качества в ряде стран, в первую очередь в Японии, стали организовывать специальные кружки качества. Для того, чтобы вооружить каждого работника, независимо от уровня его образования, четкими и простыми в исполнении статистическими методами контроля качества, в Японии в начале 60-х годов из множества статистических методов были выбраны семь наиболее эффективных и доступных статистических методов, в совокупности составляющих систему, полностью обеспечивающих осуществление статистического контроля на рабочем месте. Они получили название "Семь методов (или инструментов) контроля качества" и составили основу TQC [1,3]. Это следующие статистические методы:
1)расслаивание,
2)контрольная карта,
3)контрольный лист,
4)графики (полигон, гистограмма, кумулятивная кривая),
5)диаграмма Парето,
6)причинно-следственная диаграмма (диаграмма Исикавы),
7)диаграмма разброса (поле корреляции).
Заслуга японских ученых, и, в первую очередь, профессора Исикавы, состоит в том, что они обеспечили простоту, наглядность, визуализацию этих методов, превратив их фактически в эффективные инструменты контроля качества. Их можно понять и эффективно использовать без специальной математической подготовки.
47

При всей своей простоте эти методы позволяют сохранить связь со статистикой и дают возможность профессионалам пользоваться результатами этих методов и при необходимости совершенствовать их. Можно с полной уверенностью сказать, что семь инструментов контроля качества являются необходимыми и достаточными статистическими методами, применение которых, по мнению Исикавы, помогает решить 95 % всех проблем, возникающих на производстве. Таким образом, статистические методы - это то средство, которое необходимо изучать, чтобы внедрить управление качеством. Они - наиболее важная составляющая комплексной системы контроля Всеобщего Управления Качеством.
Статистические методы контроля качества
|
|
|
|
|
|
|
|
Контрольные |
|
|
|
Контрольные |
|||
карты |
|
|
|
листы |
|||
|
|
|
|
|
|
||
Расслаивание |
|
|
|
Графики |
|||
|
|
||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
Диаграмма |
|
|
|
Диаграмма |
|||
Парето |
|
|
|
разброса |
|||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Причинно-следственная диаграмма
Семь инструментов контроля качества
48
12. Расслаивание статистических данных
Одним из наиболее простых и эффективных статистических методов, широко используемым в системе управления качеством, является метод расслаивания. Недаром он стоит в числе первых из семи статистических методов, лежащих в основе контроля и последующего анализа качества. В соответствии с этим методом производят расслаивание статистических данных, т. е. группируют данные в зависимости от условий их получения и производят обработку каждой группы данных в отдельности. Данные, разделенные на группы в соответствии с их особенностями, называют слоями (стратами), а сам процесс разделения на слои (страты) — расслаиванием (стратификацией).
Существуют различные методы расслаивания, применение которых зависит от конкретных задач. Например, данные, относящиеся к изделию, производимому в цехе на рабочем месте, могут в какой-то мере различаться в зависимости от исполнителя, используемого оборудования, методов проведения рабочих операций, температурных условий и т. д. Все эти отличия могут быть факторами расслаивания. В производственных процессах часто используется метод 4М, учитывающий факторы, зависящие от человека
(man), машины (machine), материала (material), метода (method).
Расслаивание осуществляется примерно так: расслаивание по исполнителям — по квалификации, по
полу, по стажу работы и т. д.; расслаивание по машинам и оборудованию — по
новому и старому оборудованию, по марке, конструкции, выпускающей фирме и т. д.;
расслаивание по материалу — по месту производства, по фирме-производителю, по партии, по качеству сырья и т. д.;
49
расслаивание по способу производства — по температуре, по технологическому приему, по месту производства и т. д.
Например, если расслаивание произведено по фактору «оператop» (man), то при значительном различии в данных можно определить влияние того или иного оператора на качество изделия; если расслаивание произведено по фактору «оборудование» — влияние использования разного оборудования и т. д.
Врезультате расслаивания обязательно должны соблюдаться следующие два условия:
различия между значениями случайной величины внутри слоя должны быть как можно меньше по сравнению с различием ее значений в нерасслоенной исходной совокупности;
различие между слоями (различия между средними значениями случайных величин слоев) должно быть как можно больше.
Впоследние годы вопросам повышения качества электронных средств уделяется все большее внимание. Для контроля их качества при серийном производстве применяются следующие методы контроля [1]: составление контрольных листов и контрольных карт, расслаивание статистических данных, построение графиков и некоторые другие (рис.1). Для их применения необходимо набрать достаточное количество статистических данных по параметрам качества изделий. Как правило, эти данные являются случайными величинами, группирующимися около среднего значения этих величин. Степень рассеивания определяет величину дисперсии.
Сбор и обработка статистических данных основаны на применении так называемого выборочного метода. Выборкой называют часть изделий, отобранных из общей их совокупности для получения информации обо всем количестве изделий, называемом общей или генеральной совокупностью. При этом последнее подразумевает однородную совокупность
50
