Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5628

.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

2.33 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

x 5

18 x 5

2 x 9 18

( x 5)

2x 9

lim

18 2 x 9

2x 9

				18(x		5)
			2x 9					18x	90
			2x 9	2x	9		lim	18x	90
	18			2x	9
		18						2x	9	9 .
lim 1							x

	2x 9
x	2x 9

Тема 4. Дифференциальные исчисления

Производная и дифференциал

Пусть функция у = f(x) определена на промежутке X. Возьмём точку х Х.

Дадим

значению х

приращение

0 , тогда

функция

получит приращение

f x .

Определение. Производной функции у = f(x) называется предел отношения

приращения функции к приращению переменной х,

при стремлении последнего к

нулю (если этот предел существует):

lim

f (x

x) f (x)

x 0

Основные правила дифференцирования

Если С ─ постоянное число, U

U x , V

V x ─ функции, имеющие

производные, тогда:

0 ;

(I)

V ;

(II)

(CU )

CU ;

(III)

U V

V U ;

(IV)

V U

(V)

V 2

Если у = f(u), u = φ (х) ─ дифференцируемые функции от своих аргументов, то производная сложной функции y=f[(φ(x)] существует и равна произведению производной данной функции по промежуточному аргументу на производную этого аргумента по независимой переменной х, т.е. y f (u) u (VI).

Таблица производных основных функций

№

Формула

(xn )

n xn 1

n un 1 u

)

ln a ( a 0, a 1)

)

u u

ln u

u u

loqa x

( a 0, a 1)

(loqau)

ln a

(ln x)

ln u

(sin x)

cosx

sin u

cosu

cosx

sin x

cosu

sin u

tqx

tqu

cos2 x

cos2 u

ctqx

ctqu

sin2 x

sin2 u

arcsinx

arcsinu

arccosx

arccosu

arctgx

arctgu

1 u2

arcctgx

arcctgu

Пример 14

Найти производные функций:

a) y sin cos 5x ;

3 x e3x 5 ;

c) y arctg

x 2

Решение:

а) функцию y

sin cos 5x

можно представить в виде

sin u , где

u cos5x .

Поэтому, используя

правило дифференцирования (VI)

и формулы

таблицы

производных y

(sin(u))

u cos u

(cos 5x) cos cos 5x

5 sin 5x cos cos 5x ;

b) функция y

e3x

представлена произведением

двух функций, поэтому на

основании правила (IV)

e3x

e3x 5 x3 e3x

e3x

5 3e3x x3

3e3x 3

33 x2

)

e3x

3x x

e3x 9x

;

3 3 x2

функцию

arctg

можно представить в

виде y

arctgu,

где u

x 2

1 x2

используя формулу (26) и

правила дифференцирования

(V) и (VI) получим:

2x 1 x2

2 1 x2

2x 2x

1 x2 2

1 2x2

4x2

1 x2 2

x2 2

1 x

2 2x

2 1 x

1 2x2

2 2

1 x2

Определение.

Дифференциалом функции у=f(x) называется главная, линейная

относительно

часть приращения функции, равная произведению производной

на приращение независимой переменной:

f x

x .

Дифференциал независимой переменной равен приращению этой переменной,

т.е. dx

x . Итак, дифференциал функции равен произведению её

производной на

дифференциал аргумента: dy

f x

dx .

Общая схема исследования функции и построения графика

Для

полного

исследования

функции

и построения

её

графика

рекомендуется использовать следующую схему:

1)найти область определения функции;

2)найти точки разрыва функции и вертикальные асимптоты (если они существуют);

3)исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты;

4)исследовать функцию на чётность (нечётность) и на периодичность (для тригонометрических функций);

5)найти экстремумы и интервалы монотонности функции;

6)определить интервалы выпуклости и точки перегиба;

7)найти точки пересечения с осями координат, если возможно и некоторые дополнительные точки, уточняющие график.

Пример 15

Исследовать функцию y

x 2

и построить график.

x 2

Решение:

1) область определения : x

(

; 1)

( 1;1)

(1;

) ;

2) функция терпит разрыв в точках x1

1 ,

Исследуем функцию на наличие вертикальных асимптот.

lim

;

lim

1 ─ вертикальная асимптота;

1 0 x2

lim

;

lim

1─ вертикальная асимптота;

x 1 0 x2

3) исследуем функцию на наличие наклонных и горизонтальных асимптот.

Прямая y

b ─ наклонная асимптота, если k

lim

f (x)

, b

lim ( f (x) kx) .

lim

x 2

0 , b

lim

x 2

(x 2

1)x

Прямая

1 ─ горизонтальная асимптота;

4) функция является чётной т.к.

(

x)2

y(x) . Чётность

(

x)2

функции указывает на симметричность

графика относительно оси ординат;

5) найдём интервалы монотонности и экстремумы функции:

(x2

1) (x2

1) (x2 1)

(x2 1)2

Найдём критические точки, т.е. точки в которых производная равна 0 или не

существует: 4x 0 ;	(x2 1)2 0 . Имеем три точки	x	0 ;	x	2	1; x	3	1	. Эти точки
		1			2		3

разбивают всю действительную ось на четыре промежутка. Определим знаки y

на каждом из них.

	y	+	+	─	─

		-1	0		1
			max
На интервалах (-∞; -1) и (-1; 0) функция				возрастает, на интервалах (0; 1) и
(1 ; +∞) ─ убывает. При			переходе через точку x 0		производная меняет знак
с плюса на		минус, следовательно, в этой		точке	функция имеет максимум
ymax f (0)		1;

6) найдём интервалы выпуклости, точки перегиба.

y	4x		4(3x2	1)	.
y	(x2 1)2		(x2	1)3	.

Найдём точки, в которых y равна 0 или не существует.

3x2

0 не имеет действительных корней.

0 , x

1, x

Точки

и x2 1

разбивают действительную

ось на

три интервала.

Определим знак y

на каждом промежутке.

─

-1

Таким

образом,

кривая,

на интервалах

;

1 и

выпуклая вниз и

выпуклая

вверх на интервале (-1;1); точек перегиба нет,

т. к. функция в точках

и x2

1 не определена;

найдём точки пересечения с осями.

С осью Oy график функции пересекается в точке (0; -1), а с осью Ox график не пересекается, т.к. числитель данной функции не имеет действительных корней.

-1	0	1
	-1

Рисунок 5 ─ График функции y	x 2	1

	x 2	1
	x 2	1

Тема 5. Функция двух переменных
Определение.	Если каждой паре чисел			x.y	D	по некоторому закону f
поставлено одно определённое число z			Z ,	то говорят, что на множестве D задана
функция Z=f(x,y).
Для определения полного дифференциала функции Z=f(x,y) необходимо ввести
понятие частной производной нескольких переменных.
Определение.	Величина	f x	x, y	y	f x, y	называется полным

приращением функции в точке (х, у). Если задать только приращение аргумента x или только приращения аргумента y , то полученные приращения функции

соответственно: xZ

f x

x, y

называются частными.

Определение. Частной производной от функции

x, y

по независимой

переменной x

называется конечный предел

Z x

lim

x Z

lim

x, y

x, y ,

вычисленный при постоянном y .

Определение. Частной производной

от функции

x, y

по

y называется

конечный

предел

Z y

lim

y Z

lim

f x, y

вычисленный

при

0 y

постоянном x .

Обозначается

частная

производная

так:

Z x

, Z y

или

;

f x

x, y ;

f y

x, y .

Пример 16

Найти частные производные функций:

a) Z x ln y

;

b) Z x y .

Решение:

а) при нахождении частной производной

по

будем рассматривать y как

величину постоянную.

Получим:

ln y

Аналогично, дифференцируя по у, считаем x

постоянной величиной, т.е.

Z y

x ln y

;

b) при фиксированном

y имеем степенную функцию от

х,

таким образом,

Z x

x y

при фиксированном x

функция является показательной относительно y , тогда

Z y

x y ln x .

f x dx,

F (x) C .

Полный дифференциал функции Z

f x, y

вычисляется по формуле

dy .

Пример 17

Найти полный дифференциал функции

x 4

5x 2 y

2 y 3 .

Решение:

4x3

10xy ;

5x 2

6 y 2

5x 2 6 y 2 ;

dZ 4x3 10xy

dx 5x 2 6 y 2 dy .

Тема 6. Интегральные исчисления

Неопределённый интеграл

Определение. Функция F(x) называется первообразной функцией для функции ƒ(х) на промежутке X, если в каждой точке x этого промежутка

F/ (x) = f(x).

Если функция f(x) имеет первообразную F(x), то она имеет бесконечное множество первообразных, причём все первообразные содержатся в выражении F(x) + С, где С ─ произвольная постоянная.

Определение. Совокупность всех первообразных функции ƒ(х) на промежутке X называется неопределённым интегралом от функции f(x) и обозначается т.е. f (x)dx

			Свойства неопределённого интеграла
1.	a f	x dx a	f x dx , a ─постоянное число.
2.	f1 x	f 2 x	f3 x dx	f1 x dx	f 2 x dx	f3 x dx .

3. d[f x dx] f x dx .

4.f x dxf x .

5.dF x F x C .

Таблица основных интегралов

№

Формула

№

Формула

cos xdx

sin x

ctgx

sin

n 1

C ,

tgx

n 1, n const

cos2 x

arcsin

a 2

x 2

a x dx

a x

C , a

0, a

arctg

ln a

e x dx e x

x 2

a 2

x a

sin xdx

cos x

x 2

Пример 18

1 2

Найти интеграл

dx .

Решение :

1 2

4x 4

x 1

4 4

2 dx 4

2 dx 8x 2

4 x

4 ln

Таблицу интегралов можно расширить, если применить формулы:

а)	f ax	b dx	1	F ax b C , если		f x dx F x C ;
			a

	x
б)		dx ln	x		C .
	x

Пример 19

Найти интегралы.

а)	e 4x		5dx		1	e 4x	5 C ;	б) sin 3x 2 dx				1	cos 3x 2 C ;


				4								3
в)		dx		1			2dx	1	ln	3 2x	C ;

	3		2x	2		3	2x	2

г)

x dx

1 10x dx 1

C .

5x 2

3 10 5x 2 3 10

Замена переменной в неопределённом интеграле (метод подстановки)

Одним из основных методов интегрирования является метод замены переменной, описываемый следующей формулой:

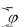
f x dx f tt dt ,

где x t ─ функция, дифференцируемая на рассматриваемом промежутке.

Пример 20

Найти интегралы:

x 2 3

2x3 4 dx ; б)

arctg

dx;

2 sin x dx

а)

;

в)

г)

1 x2

cos2 x

2x3

t 5

Решение: а)

x 2 3

2x3 4 dx

6x 2 dx

t 4 dt

3 2x3 5

C ;

x 2dx

x 2 dx

б)

3x 2 dx

arcsin t C

arcsin x3

C ;

x 6

x 2 dx

t 2

arctg3 x

arctgx

t 4

arctg4 x

в)

t 3dt

C ;

x 2

2 sin xdx

cos x

sin xdx

2 ln

t 2

г)

cos 2 x

t 2

sin xdx

2 ln

cos x

cos 2 x

Интегрирование по частям

Интегрированием по частям называется нахождение интеграла по формуле

		U dV U V V dU ,
где U	x , V	x ─ непрерывно дифференцируемые функции.

При использовании этой формулы за U берется та функция, которая при дифференцировании упрощается, а за dV - та часть подынтегрального выражения,

интеграл от которой известен или может быть найден.

Пример 21.

Найти интегралы:

x e7x dx;

б)

x3 ln x dx ;

в) arctgx dx .

Решение:

x e7xdx

dx;

x e7 x

e7 xdx

7 x

dx;

7 e

;

x e7 x

e7x

ln x ;dU

dx;

б)

x3 ln xdx

x4 ln x

ln x

dV x3dx; V

x3dx

;

arctgx;

;

в)

arctgxdx

arctgx

dx x

arctgx

ln( x

1) C.

dx;

1 x2

Определенный интеграл Формула Ньютона – Лейбница

Если функция f(x) непрерывна на отрезке [а;b] и F(x) ─ первообразная для f(x) на этом отрезке, то справедлива формула Ньютона ─ Лейбница

f (x)dx F (x)

	a	F (b) F (a) .
	b	F (b) F (a) .
	b

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20222.31 Mб35623.pdf
#
13.11.20222.31 Mб535624.pdf
#
13.11.20222.31 Mб335625.pdf
#
13.11.20222.31 Mб15626.pdf
#
13.11.20222.31 Mб95627.pdf
#
13.11.20222.33 Mб65628.pdf
#
13.11.20222.34 Mб45629.pdf
#
13.11.20222.35 Mб35630.PDF
#
13.11.20222.37 Mб85631.pdf
#
13.11.20222.37 Mб95632.pdf
#
13.11.20222.38 Mб55633.pdf