Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2402

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 125 6 7 8 9 10 11 12 > Следующая >>>

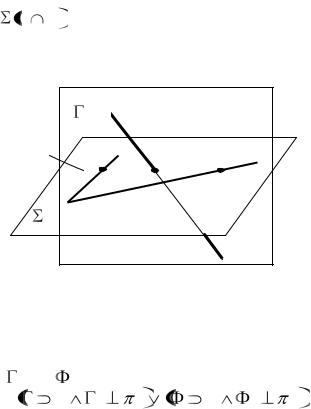
Рис. 12.7. Пространственная модель пересечения прямой и проецирующей плоскости

На эпюре Монжа: прямая a пересекается с горизонтально-проецирующей плоскостью в т. K1 (рис.12.8,а).

	K1 a		F .
				2		b2
					K2	b2		E2
			a					E2
			a	2
				2
						2
x		F			K1
		F	1		K1	b1
						b1		E1
		a					б)	E1
			1		а)		б)
					а)

Рис. 12.8. Эпюр Монжа пересечения прямой с горизонтальнопроецирующей плоскостью (а) и с фронтально-проецирующей плоскостью (б)

Аналогично – для фронтально-проецирующей плоскости (рис. 12.8, б).

12.5. Пересечение плоскости общего положения с проецирующей плоскостью

Такое пересечение определяется по точкам пересечения 2-х любых прямых линий плоскостями общего положения с проецирующей плоскостью.

a // b пересекается с фронтально-проецирующей плоскостью (рис. 12.9).

	g1	a2	b2
			b2
2
2	E2
	E2		K 2

x	g1
	K1
E1	b
	1
	a1

Рис. 12.9. Пересечение плоскости общего положения с фронтально-проецирующей

Т. E2 и	т. K2 - на пересечении прямых a2 и b2
пересечение с	.
	2
	44

Находим т.		E1 и т.		K1 , соединяем и получим искомую
линию g1
12.6. Пересечение двух прямых линий
	с плоскостью общего положения
Это одна из основных задач НГ.
В решении таких задач используют проецирующую
плоскость, как секущую.
Задача	12.7.		Дано:	прямая g и плоскость общего
положения	a	b	(Рис.12.10).
Найти: точку их пересечения.
			Решение
				g
	c		A	K	B


	Рис. 12.10. Пересечение прямой и
	плоскости общего положения

Задача решается в следующей последовательности:

1) через прямую g проводим одну из проецирующих плоскостей или

g 2

2 ;

2) определяем линию пересечения заданной плоскости с вспомогательной проецирующей плоскостью или .

Она

определяется по т.					A и т. B пересечения прямых a и b
в плоскости		с плоскостью					или
A	a			;	B	b	; C	;
3)	определяем			е.	K	пересечения плоскостей		и
, т. е.		K	c	g .
Точка		K	общая		для		пересечения прямой g	и
плоскости		и является искомой точкой пересечения прямой с

плоскостью.

Задача 12.7. Дано: a b и g .

Найти: т. K .

Решение

1)Прямую g заключаем в проецирующую

плоскость (Рис. 12.11). g 2 .

c2 g2 b2

		B2
		K2
		A2			a2



x					a1
		A1
	K1		46
	K1		46
				B1	b1
					b1

c1 g1

		Рис. 12.11. Решение задачи 12.7
	2)	Определяем		линию	c пересечения			с	:
a1	1	A1 ; b1	1	B1 ; A2	a2 ; B2	b2 ; AB			.
	3)	Определяем т.		K пересечения прямой g				с прямой
AB (линией пересечения двух плоскостей): K							g	.
	Точка K является искомой точкой					K	g	.

12.7. Линии пересечения двух плоскостей общего положения

Прямую линию пересечения двух плоскостей можно определять по двум общим точкам. Для этого определяются точки пересечения двух любых прямых одной плоскости с другой, или точки пересечения прямой на каждой из плоскостей с другой плоскостью.

Задача 12.8

Дано: a b , AB AC (рис.12.12)

Определить: g .

Решение

Рис. 12.12. Решение задачи 12.8 1) Выбирают произвольно секущую вспомогательную

горизонтальную плоскость . пересекает		и	по точкам
1, 2, 3, 4.	пересекает заданные плоскости по прямым 12 и
34. точка их пересечения – т. K .
2)	Вводим вторую секущую плоскость	,	аналогично

находим точку т. E

EK -естьискомаялинияпересечениядвух заданных плоскостей. Задача 12.9. Построить линию пересечения двух

плоскостей, заданных треугольниками (12.13). Определить видимость линии пересечения.

Решение

Строим пересечение двух сторон одного треугольника с

плоскостью второго.
Через D1E1	проводим	горизонтально-проецирующую
плоскость 1 .
Определим пересечение		с ABC .
Т. M - точка пересечения сторон DE с			ABC .
Аналогично	находим точку N -		пересечения	1
				1

(проходящую через прямую E1K1 ).

После построения определяют видимость пересекающихся плоскостей. На фронтальной плоскости она может быть определена с помощью фронтально конкурирующих точек. Для определения видимости на горизонтальной плоскости проекций используют горизонтально конкурирующие точки.

Две плоскости в общем случае могут пересекаться в бесконечности. Тогда имеет место параллельность плоскостей. При этом следует учесть, что у параллельных плоскостей две

пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

Рис.12.13. Решение задачи 12.13

Вопросы для самопроверки:

1.Принадлежность точки линии, поверхности.

2.Как построить пересечение двух плоскостей, заданных треугольниками?

13. МЕТРИЧЕСКИЕ ЗАДАЧИ

Метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Все виды сводятся к двум видам задач:

а) задачи на определение расстояний между двумя точками;

б) задачи на нахождение угла между двумя пересекающимися прямыми.

Вид а) уже рассматривали, а для того, чтобы перейти к второму, необходимо рассмотреть теорему о прямом угле:

Если одна из сторон угла параллельна плоскости проекций, а другая сторона не перпендикулярна ей, то

прямой угол проецируется в виде прямого угла.

	А	В
		В
1	С1
1
	А1
	K	В1
		В1
	L
	Рис. 13.1. Теорема о прямом угле

		Доказательство
Пусть CB //	1	CB // C1B1(рис. 13.1.).
Прямая ФС пересекает свою проекцию				A1C1 в точке
K .
Через т. K проведем прямую KL // C1B1.
KL // C1B1
C1B1 // CB		KL // CB
т.к. CB		KC	KL KC .
Следовательно: KL			KCC1, т.е. KL	KC1, а так
как C1B1 // KL	C1B1		KC1 , т.е. теорема доказана.