3237

производные функции

f (x) до

второго порядка

включительно.

Пусть найдено некоторое приближенное значение xn

корня . Положим

xn

hn ,

(4.4)

f ( )

f (x

h

)

f (x

)

f (xn )

h

f c

h

2

,

(4.5)

n

n

n

n

1!

n

2!

где hn

xn ,

c

( , xn ) .

В малой окрестности точного решения

f

c

h2

имеет

2!

n

второй

порядок

малости

относительно

hn ,

поэтому

приближенно можно записать 0

f (xn )

f (xn )hn ,

откуда

hn

f (xn )

и

xn

f (xn )

.

f (xn )

f (xn )

Эта формула подсказывает следующие итерации:

xn 1

xn

f (xn )

,

n 0,1,2,... ,

(4.6)

f

(xn )

соответствует скорости геометрической прогрессии.

Рис.

9

указывает

на следующее достаточное условие

сходимости итераций.

Теорема.

Пусть функция

f (x)

дважды

дифференцируема на отрезке

a, b , причем

f (a)

f (b) 0

и

f (x)

0,

f

(x)

0

x [a,b]. Тогда для любого начального

приближения

x0 [a;b] ,

удовлетворяющего

неравенству

f (x0 ) f (x0 )

0

последовательность

(4.6)

сходится

к

единственному на

a, b

корню

уравнения

f (x)

0 .

То есть, итерации сходятся к корню с той стороны, с

которой

f (x) f

(x)

0 (рис.9). Вообще

же,

если нулевое

приближение

x0

выбрано достаточно близко к корню,

ньютоновские итерации сходятся.

Для оценки погрешности

n

- го

приближения корня

можно получить неравенство

xn

M 2

xn

xn 1

2

,

где

M 2

max

f

(x)

и

2m1

x [a;b]

xn

xn 1

,

m1

min

f (x)

.

То

есть,

если

то

x [a;b]

xn

M 2

2

,

т.е.

погрешность

очередного

приближения

2m1

xn

xn 1

0

2m1

.

M 2

Трудность в применении метода Ньютона состоит в

выборе начального

приближения

x0 , которое

должно

находиться достаточно близко к значению корня .

Поэтому

процесса, то вычисляются величины

f (xn 1 ) , f

(xn 1 ) и

следующее приближение

xn

xn 1

f (xn 1 )

.

f (xn 1 )

При выполнении условия

xn

xn 1

0 принимаем за

приближенное значение корня

значение xn

с точностью .

Достоинства метода. 1. При выполнении условий теоремы

высокая скорость сходимости вблизи простого корня.

2. При больших

значениях

f

(x)

метод

Ньютона

Пример. f (x)

x 2

a

0 .

Тогда

формула

(4.6) дает

xn 1

xn

xn2

a 1

xn

a

,

т.е.

уже

рассмотренная

2xn

2

xn

формула.

4.6.

Метод хорд

Пусть дано уравнение

(4.1),

где

f (x) – непрерывная

дважды дифференцируемая функция на отрезке

a, b . Пусть

для определенности

f (x)

0 при a

x

b .

Тогда кривая

будет

выпукла

вниз.

Возможны

два случая:

1)

f (a) 0

промежуток изоляции корня можно принять x1,b .

Соединив

точки

A1 (x1, f (x1 )) и

B(b, f (b)) , получим

в точке

пересечения хорды

с осью

OX

второе приближение x2 ,

которое вычислим по формуле

x

2

x

(b

x1 ) f (x1 )

. Если же

1

f (b) f (x1 )

f (x1) 0 , то применим эту

формулу

к

отрезку

a, x1 .

xn 1

xn

(b

xn ) f (xn )

.

(4.7)

f (b) f (xn )

Во втором

случае

неподвижен

конец

a , а

последовательные приближения имеют вид

xn

1

a

(xn

a) f (a)

.

(4.8)

f (xn )

f (a)

Если

x

-

точный

корень

уравнения

(4.1),

изолированный

на

отрезке

a, b ,

а

- приближенное

x

f (a)

f (b)

max

f

(x)

.

(4.9)

2

f (x) 3

a,b

Пример. Методом хорд найти положительный корень

уравнения x3

0.2x 2 0.2x

1.2

0 с точностью до 0.002 .

Решение.

Найдем интервал изоляции корня.

Так как

f (1)

0.6

0 и

f (2)

5.6

0 , то искомый корень

лежит в

интервале

(1,2).

Для

того

чтобы

уменьшить количество

вычислений

разделим

этот

интервал

пополам.

Так как

f (1.5)

1.425

0 ,

1

1.5 .

Последовательно

применяя

формулу (4.7),

будем иметь

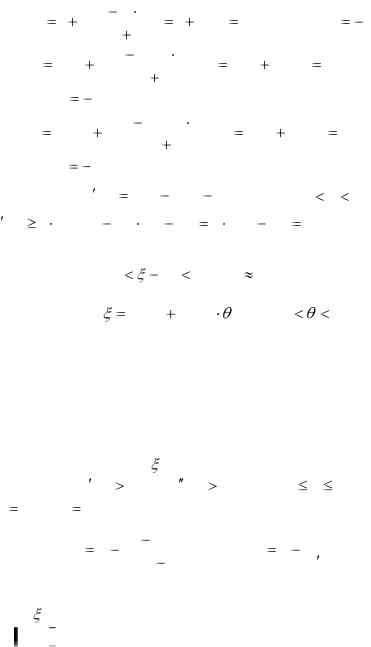
x1

1

(1.6

1)

0.6

1

0.15

1.15;

f (x1)

0.173;

1.425

0.6

x2

1.15

(1.5

1.15)

0.173

1.15

0.040

1.190;

1.425

0.073

f (x2 )

0.036;

x3

1.190

(1.5

1.190)

0.036

1.15 0.008 1.198;

1.425

0.036

f (x3 )

0.0072;

Так как

f (x)

3x2

0.4x

0.2

и при x3

x

1.5 имеем

f (x) 3 1.1982

0.4 1.5

0.2

3 1.43

0.8

3.49 ,

то можно

принять

0

x3

0.0072

0.002 .

3.49

Таким образом,

1.198

0.002

,

где 0

1.

4.7. Комбинированный метод

Иногда

для

нахождения

приближенного

значения

корня

целесообразно

использовать

смешанные

методы.

Рассмотрим

этот

прием

на

примере

метода

хорд и

этапе которого находим значения по недостатку

и значения по

избытку точного корня

уравнения (4.1).

Пусть f

(x)

0 и

f

(x)

0 при

a

x

b . Полагаем

x0 a ,

x0

b получим

x

a

(b a) f (a)

,

x

b

f (b)

.

1

f (b)

f (a)

1

f (b)

Значения x1

и x1 , лежат по разные стороны от искомого

корня

(так как

f (x1 )

и

f (x1 )

имеют разные знаки). Далее

xn

1

xn

(xn

xn ) f (xn )

,

(n

0, 1, 2, ...) .

f (xn )

f (xn )

xn

1

xn

f (xn )

,

(n

0, 1, 2, ...) .

f (xn )

Пример.

Вычислить

с

точностью

до

0.0005

положительный корень уравнения x5

x

0.2

0 .

Решение.

Так как f (1)

0 и

f (1.1)

0 , то корень

лежит

в интервале (1; 1.1), т.е.

1

1.1.

Имеем:

f

(x)

5x4 1

и

f (x)

20x3 .

В

выбранном нами интервале

f

(x) 0 ,

f

(x) 0 ,

т.е.

знаки

производных сохраняются.

Применим

комбинированный метод, полагая x0

1 и

x0

1.1 .

Так как

f (x0 )

f (1)

0.2 ; f (x0 )

f (1.1)

0.3105;

f

(x0 )

f

(1.1)

6.3205,

то формулы (4.6) и (4.8)

дают:

x

1

0.1 0.2

1.039 ;

x

1.1

0.31051

1.051.

1

0.51051

1

6.3205

Ввиду

того,

что

x1

x1

0.012, то точность

недостаточная.

Находим следующую пару приближений:

x2

1.039

0.012 0.0282

1.04469, x2 1.051

0.313

1.04487.

0.0595

5.1005

Здесь

x2 x2

0.00018,

т.е. нужная

степень

точности

f1

(x1, x2 ) 0

(4.10)

f2 (x1, x2 ) 0.

(x(n) , x(n) ) - приближенное решение на n -м шаге. Тогда точное

1

2

решение можно представить в виде.

1

x(n)

n

и

2

x(n)

n ,

где

(n) ,

n

-

поправки

1

1

2

2

1

2

(погрешность решения). Пусть функции

f1 x1, x2

и

f2 x1, x2

f

1

(

1

,

2

)

f

1

(x(n)

(n) ; x(n)

(n) )

1

1

2

2

f

1

(x(n)

, x(n) )

df (x(n) , x(n) )

o (

(n) ,

(n) )

1

2

1

1

2

1

1

2

f

2

(

1

,

2

)

f

2

(x(n)

(n) ; x(n)

(n) )

1

1

2

2

f

2

(x(n) , x(n) )

df

2

(x(n) , x(n) )

o

2

(

(n) ,

(n) ).

1

2

1

2

1

2

Отбрасывая

слагаемые

o

(n)

(

(n)

,

(n) )

и

1

1

2

o2(n) ( 1(n) , 2(n) ) ,

получаем,

что точное

решение

(

1, 2 )

определяется через приближенное решение

x(n)

(x(n) , x(n) )

1

2

из решения линейной системы:

f1

(n)

f1

(n)

f1

x1

1

x2

2

f 2

(n)

f 2

(n)

f 2 .

x1

1

x2

2

Учитывая,

что

(n)

1

x(n)

и

(n)

2

x(n) ,

1

1

2

2

определению приближенного решения

x(n 1)

(x(n 1)

, x(n 1) )

1

2

по приближению

x(n)

(x(n)

, x(n) ) ,

как решение следующей

1

2

системы линейных относительно x(n)

, x(n) уравнений:

1

2

f1

(x(n 1)

x(n) )

f1

(x(n 1)

x

(n) )

f

1

1

2

2

1

x1

x2

(4.11)

f2

(x1(n 1)

x1(n) )

f2

(x2(n 1)

x2(n) )

f2 .

x1

x2