новая папка 1 / 773161
.pdf
(произвольное постоянное принято равным нулю, поскольку нам достаточно иметь какой-нибудь один интегрирующий множитель).
|
|
∂M |
− |
∂N |
|
Очевидно, что в этом случае выражение |
∂y |
|
∂x |
не зависит от y. |
|
|
N |
|
|||
|
|
|
|
|
|
|
∂M |
− ∂N |
|
|
|
Имеет место и обратное: если выражение |
∂y |
∂x |
не зависит от y, то |
||
|
N |
|
|||
|
|
|
|
|
|
существует интегрирующий множитель μ, который зависит только от x. 2) Пусть µ = µ(y), тогда
|
dµ |
( |
y |
) |
|
∂ |
M |
|
|
= −µ |
M |
||
dy |
|
|
∂y |
|||
|
|
|
|
|||
или
dµ(y) |
|
∂M |
− |
∂N |
|
∂ |
∂ |
||
|
= − |
y |
|
x |
µ(y) |
|
M |
|
|
|
|
|
откуда
−∂N , ∂x
dy,
|
|
∂M |
− |
∂N |
|
|
|
|
|
−∫ |
∂y |
|
∂x |
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
M |
|
|
|||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
, |
µ(y)= e |
|
|
|
|
|
|
|
|
где положено c = 0.
В этом случае выражение
(5.3)
∂∂My − ∂∂Nx не зависит от x и, обратно, если
M
выражение не зависит от x, то интегрирующий множитель μ, зависящий только от y, существует.
Для приведения уравнения (4.1) к уравнению в полных дифференциалах в рассматриваемых частных случаях поступают так. Составляют вы-
ражение ∂∂My − ∂∂Nx и берут его отношение к N. Если это отношение не за-
висит от y, то для нахождения интегрирующего множителя следует пользоваться формулой (5.2). В противном случае берут отношение выраже-
21
ния ∂∂My − ∂∂Nx к M: если это отношение не зависит от x, то существует множитель μ, не зависящий от x, и его можно найти по формуле (5.3).
Пример 3. Найти интегрирующий множитель дифференциального уравнения
(x2 − y)dx +(x2 y2 + x)dy = 0
ипроинтегрировать его.
Решение. В нашем случаеM (x; y)= x2 − y; N (x; y)= x2 y2 + x,
∂∂My = −1; ∂∂Nx = 2xy2 +1; ∂∂My − ∂∂Nx = −2(1+ xy2 ).
Отношение
Отношение
∂∂My − ∂∂Nx
M
∂∂My − ∂∂Nx
N
= |
|
−2 |
(1+ xy2 ) |
|||
|
x2 − y |
|||||
|
|
|
|
|||
= |
|
−2 |
(1+ xy2 ) |
|||
|
x |
( |
xy2 |
+1 |
||
|
|
|||||
|
|
|
|
) |
||
зависит от x и y.
= − 2x зависит только от x.
Следовательно, интегрирующий множитель может быть найден по формуле
µ(x)= e−2∫dxx = e−2ln x = x12 .
Умножив обе части уравнения на x12 , получим
|
y |
|
|
2 |
|
1 |
|
2 |
|
xdy − ydx |
|
||
1− |
|
|
dx + y |
|
+ |
|
dy = 0, |
dx + y |
dy + |
|
2 |
= 0. |
|
x |
2 |
|
x |
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
22
Так как |
xdy − ydx |
|
|
y |
|
то общий интеграл получается путем ин- |
||||||||
|
|
|
|
|
= d |
|
|
|
, |
|||||
|
|
x |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
тегрирования в виде |
|
|
|
|
|
|
||||||||
x + |
y3 |
+ |
|
y |
= |
c |
или 3x2 |
+ xy3 +3y −cx = 0. |
||||||
3 |
|
x |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
УПРАЖНЕНИЯ (2)
1)(yex +3y)dx +(ex +3x)dy = 0.
2)1+ y2 dx −2 y dy = 0.x2 x
3) (4x3 +3x2 y + y3 )dx +(x3 +3xy2 + 4y3 )dy = 0.
4) yexy dx +(1+ xexy )dy = 0.
5) 2xydx +(x2 + 2y2 )dy = 0.
6) x2dy − y2dx = 0.
(x − y)2
7) |
y4dx +(4xy3 + y)dy = 0. |
|||
8) |
|
1 |
|
4 |
|
2y2 x3 |
+1 dx +3x3 ydy = 0. |
||
|
|
|
|
|
9)(2x + y2 cos x)dx + 2ysin xdy = 0.
10)(2xey +1)dx +(ey x2 +1)dy = 0.
11)2xsin ydx +(2y + x2 cos y)dy = 0.
12)(2xy2 +cos x)dx + 2x2 ydy = 0.
23
13)sin 2xdx = 2cos(x + y)(dx + dy).
14)(y2 sin x + x)dx +(e2 y −2y cos x)dy = 0.
15)(y +sin 2x)dx +(x +1)dy = 0.
x x x
16)1+e y dx +e y 1− y dy = 0.
17)2(3xy2 + 2x3 )dx +3(2x2 y + y2 )dy = 0.
18)(3 + 2y −7 y3 )dx +(2x −21xy2 + 20y3 )dy = 0.
19)xdx + ydy + xdx + ydx = 0.
x2 + y2
µ = µ(x)
20)(x2 −2y)dx + xdy = 0.
21)(x2 + y2 )dx + xydy = 0.
22)x3 (1+ln x)+ 2y dx + x(3x2 y2 −1)dy = 0.
23)(xy −1)dx + x2dy = 0.
24)ydx − x(xy +1)dy = 0.
25)(tan2 x +sin y cos x)dx = sin xcos ydy.
26)x3exdx = xdy − ydx.
27) (x2 + y cos2 x)dx = xcos2 x(1− xsin y)dy.
µ = µ(y)
28) y2 (x − y)dx +(1− xy2 )dy = 0.
24
29)y(1+ y2 )dx +(xy2 + x +1)dy = 0.
30)ydx −(x + y2 )dy = 0.
31)yexdx −(2ex + y4 )dy = 0.
32)(1+ y2 )dx +(4xy −1)dy = 0.
33)cos xdy −(y −sin x)dy = 0.
|
|
Ответы к упражнениям (1) |
|||
1. |
y = cx −c4 ; |
особый интеграл 64y3 = 27x4. |
|||
2. |
y = cx −ec ; |
особое решение y = xln x +ln2 x. |
|||
3. |
y = cx +c2 ; |
особое решение y = − |
x2 |
. |
|
4 |
|||||
|
|
|
|
||
4. |
y = cx + 1 ; |
особый интеграл y2 = 4x. |
|||
|
c |
|
|
|
|
5.y = cx +c −c2 ; особое решение y = x +1 2 .
2
6.y = cx −
1+c2 ; особый интеграл x2 + y2 =1.
|
особое решение y = x(π −arccos x + |
|
). |
7. y = cx +sin c; |
1− x2 |
8. y =1± 1+4cx +ln1± 
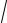1+4cx . 2x
25
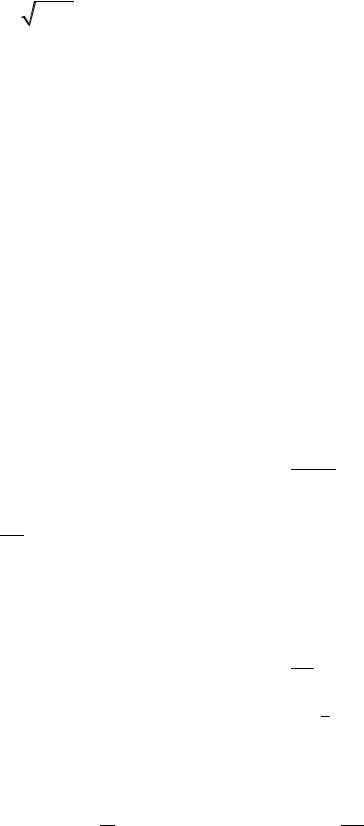
9. x = |
c |
|
+ |
2 p; |
|
y = 2c |
+ 1 p2. |
||||
p2 |
|
||||||||||
|
|
|
3 |
|
|
p |
3 |
|
|||
10. |
y =( |
|
|
+c)2 ; |
особое решение y = 0. |
||||||
|
x +1 |
||||||||||
11. |
x = c +ln p |
; |
y = 2xp + |
1 |
. |
||||||
|
|||||||||||
|
|
|
|
|
p2 |
|
|
|
p |
||
12. |
(x −c)2 + y2 = (ac)2 . |
|
|
|
|||||||
Ответы к упражнениям (2)
1.yex +3xy = c.
3.x4 + x3 y + xy3 + y4 = c.
5.x2 y + 23y3 = c.
7. xy4 + y2 = c.
2
9. x2 + y2 sin x = c. 11. x2 sin y + y2 = c.
13. sin2 x −2sin(x + y)= c.
15. xy − 12 cos2x + y = c. 17. x4 +3x2 y2 + y3 = c.
19. x2 + y2 −2arctan xy = c.
2.x2 − y2 = cx.
4.exy + y = c.
6.xxy− y = c.
8.32 x43 y2 + x = c.
10.x2ey + x + y = c.
12.x2 y2 +sin x = c.
14. x2 − y2 cos x + 1 e2 y = c. 2 2
x
16. xye y = c.
18.3x +2xy −7xy3 +5y4 = c.
20.ln x + xy2 = c.
26
21. x4 +2x2 y2 = c.
23. x = cexy .
25. tan x − sinsin xy = c.
27.tan x −cos y − xy = c.
29.xy +arctan y = c.
31.2ex = y2 (x + y2 ).
33.sin x = y −1+ce−y .
22.y3 − xy2 + xln x = c.
24.xy2 +2y = cx.
26. ex (x −1)− xy = c.
28. x2 − xy − 1 = c. 2 y
30. xy − y = c.
32. x(1+ y2 )− y − y3 = c. 3
27
Литература
1.Пискунов, Н. С. Дифференциальное и интегральное исчисление. Т. 2 / Н. С. Пискунов. — М.: Наука, 1978.
2.Смирнов, В. И. Курс высшей математики. Т. 2 / В. И. Смирнов. — М.: Гостехиздат, 1974.
3.Бермант, А. Ф. Курс математического анализа. Т. 2 / А. Ф. Бермант. — М.: Гостехиздат, 1955.
4. Шнейдер, В. Е. Краткий курс высшей математики. Т. 2 / В. Е. Шнейдер, А. И. Слуцкий, А. С. Шумов. — М.: Высш. школа, 1978.
Ответственный за выпуск Ю. В. Малышев
Подписано в печать 02.05.2017 |
Формат 60×84 1/16 |
|
Бумага офсетная |
Печать ризографическая |
1,63 усл. печ. л. |
1,75 уч.-изд. л. |
Тираж 100 экз. |
Заказ |
Издательство Казанского национального исследовательского технологического университета
Отпечатано в офсетной лаборатории Казанского национального
исследовательского технологического университета
420015, Казань, К. Маркса, 68
28