
8078
.pdf
11
площади поверхности образующей сферы (сферы, образующей тепловую волну от точки приложения нагрузки), т. е:
= ,
где = 42 – площадь поверхности образующей сферы.
Данное утверждение может быть верно для распространения фронта тепловой волны внутри тела. Если источник тепла приложен к поверхности изотропного теплопроводящего тела, то образующая фронт волны сфера отсекается, уменьшая площадь своей поверхности примерно в два раза. Таким образом, для приложения источника тепла к поверхности тела запишем:
|
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
22 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Радиус выражается из общего уравнения сферы и равен: |
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
)2 |
+ ( |
− |
)2 |
+ ( − )2. |
||||||
= √( |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
В идеале возникает случай, когда = . Более того, непрерывность представления такого закона приводит к неадекватности поведения функции на
промежутке (√21 > ≥ 0). Значение начинает превышать значение
приложенной тепловой нагрузки ( > ). Решением проблемы может стать приведение непрерывной функции к дискретному виду.
Исходим из того, что источник тепла приложен к абстрактной сферической окрестности единичной площади 1, тогда в точке приложения температуры имеем
= 1 = , где 1 = 1.
Если 1 = 42, тогда = 1 . Подведем дискретную основу для закона
2√
сферического распределения. Вводим дискретный параметр ∆ как расстояние от k-ой точки приложения тепла до рассматриваемой точки тела ( , , ). Формула вычисления площади принимает вид:
|
|
|
|
|
|
1 |
|
|
|
2 |
|
= 4 ( + ∆ )2 |
= 4 ( |
|
+ ∆ ) . |
||||||||
|
|
||||||||||
|
|
|
|
|
|
2√ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
Открыв скобки и |
перегруппировав |
|
члены |
|
правой части, получим |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + 4 |
√ |
∆ + 4 ∆ 2 |
= 1 + 2 |
|
+ 42 |
||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда для описания дискретного геометрического закона температурного
напряжения в текущей i-ой точке получаем: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( |
|
, |
|
, |
|
) = |
|
|
, где ∆ = √ 2 |
+ 2 |
+ 2 |
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
+ 42 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12
при условии, что начало системы координат располагается в точке приложения
тепла ( , , ).
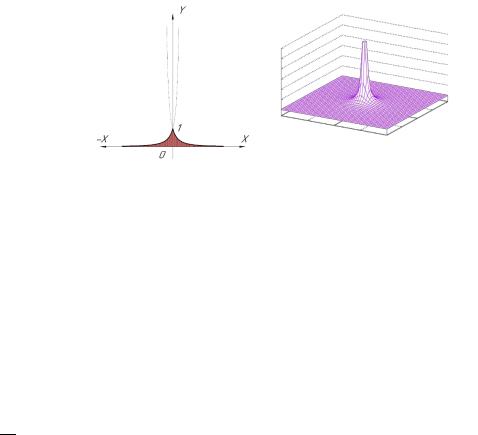
Приведенный дискретный закон отчасти соответствуют закону квадратичной гиперболы с той разницей, что при ∆ = 0 значение = . А при= 1, принимают вид, приведенный на рисунке 4. Дополнительно, на рисунке 4 закрашена область сечения подфункционального пространства , объем которого можно соотнести с количеством температуры, приложенной к телу. Таким образом, все дальнейшие расчеты при моделировании можно проводить, используя указанный эквивалентный температурный объем, а не оперировать физическим понятием температуры.
Рисунок 4 – Дискретный закон температурного напряжения Отмеченное соотношение описывается соответствием:
|
= . |
|
|
Для определения указанного |
объема подфункциональной области |
температурного напряжения необходимо вычислить четверной интеграл вида:
|
|
|
|
|
|
|
|
= ∫ ∫ ∫ ∫ |
|
|
, |
||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 + 2 |
+ 42 |
||
|
|
|
|||||
где l, w и h – размер исследуемой области ( |
). |
|
|||||
|
|
|
|
|
|
|
|
При примере области 100 × 100 × 100 и единичном воздействии значение:≈ 301 . Таким образом, модель единичного температурного напряжения можно
доопределить уравнением равновесия объемного распределения температурного напряжения. Практически, это позволяет при мгновенном приложении тепловой нагрузки распределять ее сразу, а не сосредотачивать в единице объема, т. е. при мгновенном приложении нагрузки в точке, величина нагрева точки меньше в раз.
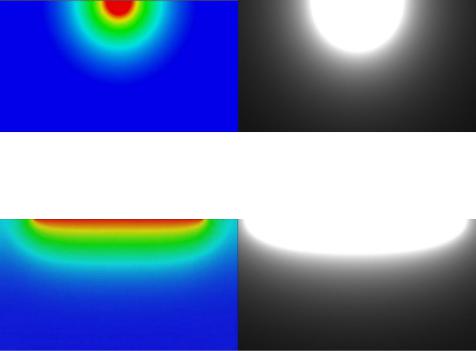
Результаты сравнения геометрии температурного напряжения, полученного МКЭ и функционально-воксельным методом (ФВМ) (см. рисунок 5 и 6) позволяют сделать предположение об адекватности полученной геометрии сформулированного дискретного закона, описывающего локальные характеристики геометрической модели распределения тепловой нагрузки.
13
МКЭ ФВМ Рисунок 5 – Сравнение распределения температурного напряжения МКЭ и
ФВМ при приложении нагрузке в точке
МКЭ ФВМ Рисунок 6 – Сравнение распределения температурного напряжения МКЭ и
ФВМ при приложении распределенной нагрузки
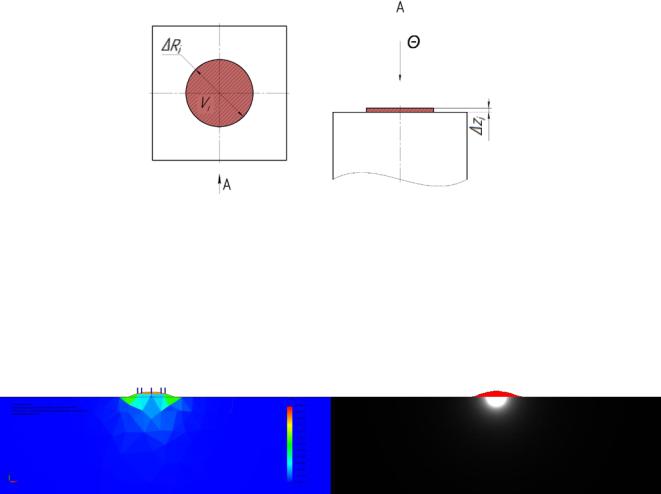
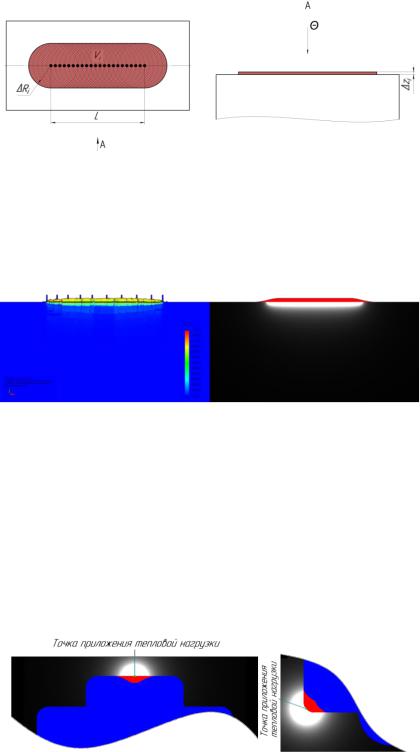
В третьей главе разработана локальная модель теплового расширения при приложении источника тепла к локальной окрестности тела (см. рисунок 7). Интерпретируя закон классической теории теплового расширения для дискретной модели, получим, что ∆V = , где – коэффициент теплового расширения, – температурное напряжение в -ой точке, а – объем сферы,
образуемой приращением радиуса ∆ . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Построение дискретной модели расширения поверхности заключается в |
||||||||||||||||||||||||||||
расчете |
координаты |
приращения, |
|
(например – |
|
∆ ), определяемой |
для |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рассматриваемой i-ой точки. А значит, полученный объем ∆V |
необходимо |
|||||||||||||||||||||||||||
поделить на значение текущей площади круга |
|
как секущей площадки с |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
радиусом ∆ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = 2 |
= 1, а значит = 1/ |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ( + ∆ )2 |
= (( |
|
|
|
) |
+ 2 |
|
|
|
∆ + ∆ 2) = 1 + 2√ ∆ + ∆ 2 |
, |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
√ |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∆ |
= |
|
|
|
|
|
|
|
|
∆V |
|
|
|
|
|
, где ∆V = . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 + 2 |
√ |
∆ + ∆ 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для определения ∆V необходимо по аналогии с выразить наращиваемый |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
объем : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
||
|
|
1 = |
|
|
3 = 1, а значит = √ |
|
|
|
|
, |
|
|
|
|
||||||||||||||
|
|
3 |
4 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
||
|
4 ( + ∆ )3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
|
= |
|
|
( 3 + 3 2∆ + 3 ∆ 2 |
+ ∆ 3) = |
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
4 |
|
|
|
|
|
3 |
|
|
4 |
2 |
|
|
|
|
|
4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= 1 + 3√ |
|
∆ + 3√( |
|
) |
|
|
∆ 2 |
+ |
|
∆ 3 |
, |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
где ∆ |
= |
|
|
2 |
+ |
2 |
+ |
|
2. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|||||
Полученный температурный объем на большом расстоянии от точки приложения тепла минимально влияет на геометрию объекта, так как радиус образующей сферы увеличивается, а температурное значение, наоборот уменьшается по гиперболическому закону. Иными словами, можно сказать, что на максимально удаленном расстоянии ∆ на текущей итерации изменение объема расширяет тело по всей площади круга радиусом ∆ .
Рисунок 7 – Визуализация теплового расширения на ∆ для текущего ∆
Визуальный анализ с результатами, полученными методом конечных элементов, визуально подтверждает сходство с результатами функциональновоксельного моделирования (см. рисунок 8). Стоит отметить, что для моделирования единичного воздействия для метода конечных элементов задавалась область, достаточная для построения сетки тела. В предложенном подходе данная проблема отсутствует.
МКЭ ФВМ Рисунок 8 – Сравнение результатов моделирования при единичном воздействии
источника тепла к поверхности тела
Разработана функционально-воксельная модель теплового расширения при приложении распределенного источника тепла к поверхности тела (см.
15
рисунок 9). Для получения теплового расширения при распределенной тепловой нагрузке необходимо применить закон теплового расширения для единичной нагрузки в каждой точке области распределения. Таким образом, изменение объема ∆ происходит при итерационном суммировании его значений, полученных смещением точки приложения тепла вдоль некоторой прямой длиной .
Рисунок 9 – Визуализация теплового расширения на ∆ для текущего ∆ с учетом распределения нагрузки
Сравнительный анализ геометрии ФВ-модели с результатами, полученными методом конечных элементов, также визуально подтверждает сходство результатов обоих методов моделирования (см. рисунок 10).
МКЭ ФВМ Рисунок 10 – Сравнение результатов моделирования при распределенном
воздействии источника теплоты к поверхности тела
Пример моделирования приложения источника тепла (как единичного, так и распределенного) к поверхности сложного контура демонстрирует возможность создания полноценного программного инструмента для учета тепловых характеристик при проходе режущего инструмента. Моделирование приложения источника тепла к различным точкам сложного контура с расчетом теплового расширения приведено на рисунке 11 и 12.
Рисунок 11 – Пример приложения тепловой нагрузки в точке участка контура
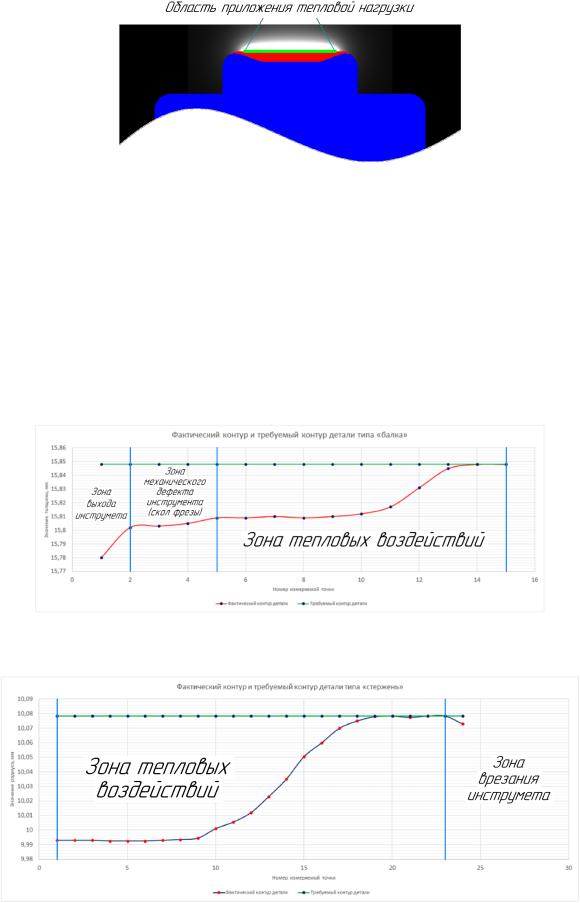
16
Рисунок 12 – Пример приложения распределенной тепловой нагрузки к указанному участку контура
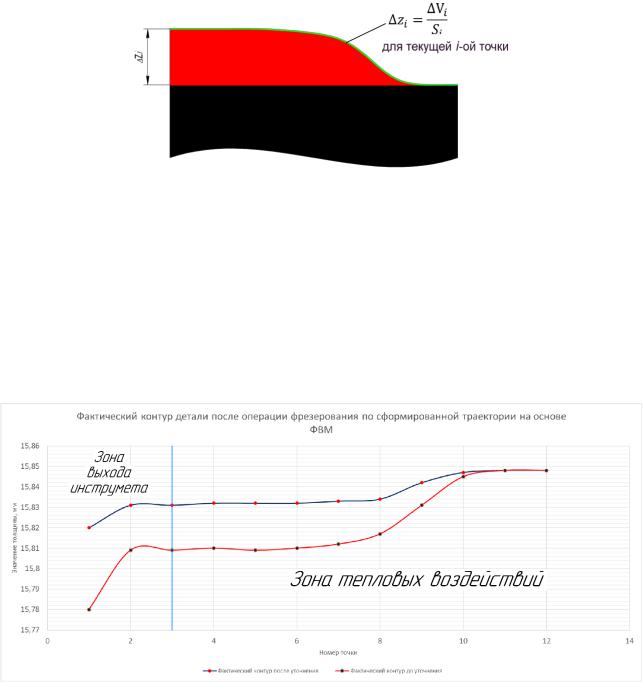
В четвертой главе проиллюстрирована возможность применения разработанных моделей и алгоритмов непосредственно при механической обработке. Для проведения экспериментов были выполнены: фрезерование заготовки типа «балка» и точение заготовки типа «стержень» на универсальном фрезерном и токарно-винторезном станках соответственно. Замер фактического контура после обработки производился после наступления теплового равновесия материала деталей с окружающей средой. А результаты отображены графически на рисунках 13 и 14.
Рисунок 13 – Результаты замера детали типа «балка» после выполнения операции фрезерования
Рисунок 14 – Результаты замера детали типа «стержень» после выполнения операции точения
17
На основании полученных данных также были установлены значения температур, влияющих на искажение формы. Именно их значения были использованы для формирования контура на основе функционально-воксельного метода для соблюдения однообразия результатов эксперимента. Результатом влияния приложения источника тепла является функциональный образ с демонстрацией формы теплового расширения и созданием контура для обхода инструментом, приведенным на рисунке 15. Для удобства восприятия формы кривой контура текущий образ отмасштабирован вдоль оси OX средствами непосредственно функционально-воксельного моделирования.
Рисунок 15 – Формирование контура для прохода обрабатывающего инструмента
Полученный контур транспонировался в код управляющей программы для фрезерного станка с ЧПУ. При выполнении операции фрезерования заготовки типа «балка», как и в случае с экспериментом на универсальном оборудовании, деталь выдерживалась для выполнения условия теплового равновесия с окружающей средой. В результате проведения замеров контура детали, эксперимент показал снижением тепловых воздействий, а контур устремлен к выравниванию, как показано на рисунке 16.
Рисунок 16 – Сравнение результатов до и после уточнения контура ФВМ
18
Основные результаты и выводы
1.Применение функционально-воксельного моделирования в решении задач учета тепловых характеристик показало свою эффективность, поскольку позволяет построить простую геометрическую модель вычисления локальной геометрии сферического затухания температурного напряжения в изотропном теле по заданной температурной нагрузке. Это позволяет расширить класс задач моделирования тепловых процессов наряду с задачами, решаемыми МКЭ.
2.Получена дискретная геометрическая модель температурного сферического затухания напряжения в изотропном теплопроводящем теле, позволяющая моделировать единичное воздействие источника тепла с получением локальных геометрических характеристик термического напряжения в теле. Такой подход гарантирует устойчивое решение, в отличии от традиционных подходов, основанных на МКЭ, что позволяет прикладывать заранее определенную температурную нагрузку в отдельно взятой точке объекта.
3.Полученная дискретная геометрическая модель расширения в точке тепловой нагрузки в изотропном теле, позволяет моделировать изменение локальных геометрических характеристик в процессе расширения материала от воздействия источника тепла с получением параметров изменения объема тела, заданного функционально-воксельной моделью. Такой подход, в отличии от традиционных подходов, основанных на МКЭ, позволяет моделировать изменение геометрии поверхности тела от теплового расширения без погрешностей, возникающих с применением расчетов МКЭ.
4.Разработан алгоритм функционально-воксельного моделирования теплового напряжения при распределенном тепловом нагружении для изотропного теплопроводящего тела. Данный алгоритм позволяет формировать геометрию тепловой волны и получать информацию о значении в точке температурного поля внутри материла.
5.Разработан алгоритм функционально-воксельного моделирования теплового расширения при распределенном тепловом нагружении для изотропного теплопроводящего тела. Данный алгоритм позволяет формировать контур (поверхность) с учетом расширения материала и получать информацию об изменении длины (объема) изделий.
6.Практическое использование разработанного подхода к созданию контура обхода инструмента при учете влияния тепловых процессов обработки показало рост эффективности обработки, т. е. приближение конечной формы детали к проектной геометрии.
7.Использование локальной геометрической модели изотропии позволяет рассматривать не только задачи тепловых процессов, но и моделировать иные физические характеристики при наличии аналитического описания физического закона.
19
Публикации по теме диссертационной работы
Статьи, опубликованные в изданиях, индексированных Scopus:
1.Plaksin, A. M. Functional-Voxel Method in Problems of Geometric Modeling of Thermal Characteristics of Objects / A. M. Plaksin, A. V. Tolok. – Текст: непосредственный // Proceedings of the 30th International Conference on Computer Graphics and Machine Vision (GraphiCon 2020): CEUR Workshop Proceedings. – 2020. – № 2744. – С. 53-64.
2.Плаксин, А. М. Визуальная диагностика физических величин на основе метода функционально-воксельного моделирования / А. В. Толок, Н. Б. Толок, А. М. Плаксин, С. А. Пушкарев, М. А. Локтев. – Текст: непосредственный // Научная визуализация. – 2020. – Т. 12. – № 3. – С. 51-60.
Статьи, опубликованные в изданиях, рекомендованных ВАК при Минобрнауки
России:
3.Плаксин, А. М. Геометрическое моделирование средств
визуализации напряжения на основе функционально-воксельного метода / С. А. Пушкарев, А. М. Плаксин, А. А. Сычева, П. М. Харланова. – Текст: непосредственный // Геометрия и графика. – 2020. – Т. 8. – № 3. – С. 36–43. – DOI: 10.12737/2308-4898-2020-36-43.
4.Плаксин, А. М. Геометрическое моделирование тепловых характеристик объектов функционально-воксельным методом / А. М. Плаксин, С. А. Пушкарев. – Текст: непосредственный // Геометрия и графика. – 2020. – Т. 8. – № 1. – С. 25-32.
Статьи в сборниках научных трудов и сборниках конференций:
5.Плаксин, А. М. Исследование тепловых процессов в зоне резания
методом функционально-воксельного моделирования / А. М. Плаксин, А. А. Сычева. – Текст: непосредственный // 17-ая Международная конференция «Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта» (CAD / CAM / PDM – 2017): сборник научных трудов / ИПУ РАН. – Москва,
2017. – С. 84-88.
6.Плаксин, А. М. Метод функционально-воксельного моделирования в
задачах исследования тепловых явлений при механической обработке / А. М. Плаксин, А. А. Сычева. – Текст: непосредственный // 17-ая Международная конференция «Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта» (CAD / CAM / PDM – 2017): тезисы конференции / ИПУ РАН. – Москва, 2017. – С. 33-33.
7. Плаксин, А. М. Моделирование тепловых характеристик на основе функционально-воксельной модели с предварительным определением контура обхода / А. М. Плаксин, А. А. Сычева. – Текст: непосредственный // 13-ое
20
Всероссийское совещание по проблемам управления (ВСПУ XIII): сборник научных трудов / ИПУ РАН. – Москва, 2019. – С. 3179-3185.
8.Плаксин, А. М. Применение воксельных структур в задачах
интеллектуализации систем автоматизированного проектирования / А. М. Плаксин, С. В. Васенков, А. В. Толок. – Текст: непосредственный // Международная школа молодых ученых и специалистов в области робототехники, производственных технологий и автоматизации. Металлообработка: сборник научных трудов / ФГБОУ ВО МГТУ Станкин. – Москва, 2016. – С. 67-69.
9.Плаксин, А. М. Применение гомотопии на основе многочлена Бернштейна в построении набора промежуточных поверхностей для обработки деталей сложной формы / А. М. Плаксин, А. В. Михайленко, А. В. Толок. – Текст: непосредственный // Информационные технологии в проектировании и производстве. – 2019. – № 2 (174). – С. 48-51.
10.Плаксин, А. М. Применение функционально-воксельной модели к моделированию тепловых характеристик / А. М. Плаксин, А. А. Сычева. – Текст: непосредственный // 18-ая Международная конференция «Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта» (CAD / CAM / PDM – 2018): сборник научных трудов / ИПУ РАН. – Москва, 2018. – С. 92-96.
11.Плаксин, А. М. Разработка трехмерных моделей для учебно-
тренировочных средств космического комплекса / А. М. Плаксин, С. В. Бронников, С. А. Кузин, М. А. Локтев, Д. В. Павлов [и др.]. – Текст: непосредственный // Космическая техника и технологии. – 2019. – № 3 (26). – С. 69-76.
12.Плаксин, А. М. Функционально-воксельная модель в задачах
интеллектуализации систем автоматизированного проектирования / А. М. Плаксин, А. В. Толок // Вестник МГТУ Станкин. – 2017. – № 2 (41). – С. 75-78.
13. Плаксин, А. М. Функционально-воксельное моделирование тепловых характеристик / А. М. Плаксин, А. А. Сычева. – Текст: непосредственный // 18-ая Международная молодежная конференция «Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта» (CAD / CAM / PDM – 2018): тезисы конференции / ИПУ РАН. – Москва, 2018. – С. 36-36.
