8504

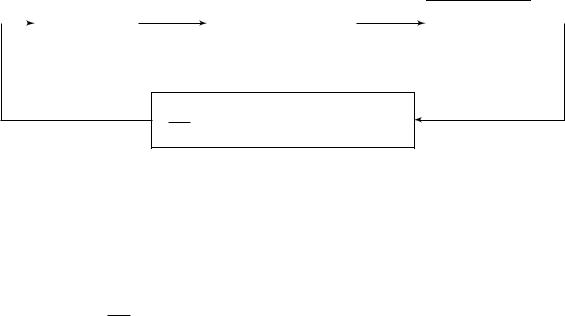
и применяя к нему необходимое условие устойчивости, получаем следующую систему неравенств:

Очевидно, что последние два неравенства несовместны, поэтому задача синтеза стабилизирующего регулятора вида (2.20) не имеет решения. Следовательно, управление необходимо искать в более широком классе, чем класс линейных обратных связей по выходу. Например, использовать наблюдатель, позволяющий восстановить компоненты вектора состояния по измеряемому выходу, после чего искать управление в виде линейной обратной связи, но уже по восстановленному состоянию

(см. рис. 2.7).

= + + −

Рис. 2.7. Структурная схема системы с наблюдателем.

Прежде чем приступать к реализации описанного подхода, напом-

ним, что наблюдателем (или наблюдателем полного порядка) для объек-

та (2.7), (2.19) называется система вида

где — состояние наблюдателя, размерность которого совпадает с размерностью состояния системы (2.7), а матрица — матрица коэффициентов усиления наблюдателя. Известно [Kwakernaak1977, Andreev1976], что ошибка восстановления = − стремится к нулю независимо от ее начального состояния тогда и только тогда, когда матрица − асимптотически устойчива. В этом случае говорят, что наблюдатель является асимптотически устойчивым. Собственные числа матрицы − называются полюсами наблюдателя. Таким образом, синтез наблюдателя состоит в определении такой матрицы коэффициентов усиления , при которой полюса наблюдателя будут расположены в левой полуплоскости комплексной плоскости. Данная задача разрешима, если пара мат-

41

риц , является детектируемой [Kwakernaak1977].

Проверим детектируемость системы (2.7), (2.19). Для этого вычис-

Следовательно, система является наблюдаемой, поэтому задача синтеза наблюдателя разрешима. Далее, согласно теореме о разделении, задачи синтеза модального регулятора (определения матрицы Θ) и наблюдателя (вычисления матрицы ) могут решаться независимо [Andreev1976]. Поскольку матрица Θ уже была найдена ранее, то осталось найти матрицу .

Предположим, что требуется передвинуть собственные числа 3 и4 матрицы , например, в точки −2 ± 0.5 . Сведем задачу построе-

42

Применяя построенное преобразование к матрицам , и получаем:

Поскольку в матрице больше одного столбца, то задача построения матрицы имеет не единственное решение. Будем искать , например, в виде:

6.376 + 0.156 1 0.156 2 − 1 − 2

совпадают с −2±0.5 . Запишем характеристический многочлен матрицы и воспользуемся теоремой Виета, тогда:

Решая данную систему, находим матрицу усиления наблюдателя

−70.795 −0.667 0 0= −70.795 −0.667 0 0 .

Возвратимся к исходным переменным:

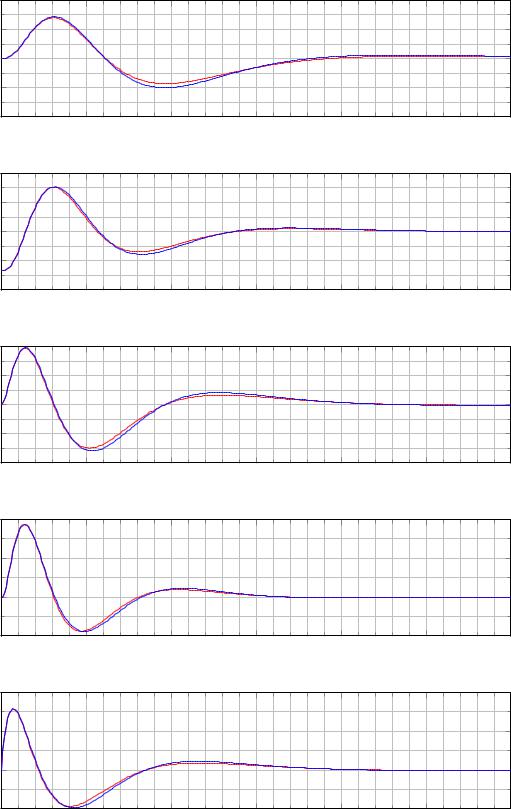
На рисунке 2.8 приведены графики переходных процессов и управления в линейной (2.7) и нелинейной (2.4) системах, замкнутых регулятором (2.12) и наблюдателем (2.22). Как и предсказывает теория, в линейном случае построенный наблюдатель позволяет восстановить состояние системы и стабилизировать. Однако в нелинейном случае

43

Наконец, рассмотрим случай, когда измеряемый выход содержит только угол отклонения маятника, то есть

взять следующую матрицу:

0 0 0

1 0 01 = 0 1 0 .

0 0 1

Очевидно, что оставшиеся блоки 3 и 4 отсутствуют, поэтому итоговая матрица преобразования, приводящего систему к каноническому разложению Калмана, имеет вид:

45

Матрицы системы (2.7) после замены принимают следующий вид:

Таким образом, ненаблюдаемое подпространство представляет собой линейную оболочку вектора 0, 0, 0, 1 и, если вернуться к исходным переменным, то

Полученный вектор как раз и соответствует переменной , что доказывает ее ненаблюдаемость. Окончательно заключаем, что синтезировать асимптотически устойчивый наблюдатель по выходу (2.23) для системы (2.7) невозможно, поскольку собственное число = 0 нельзя передвинуть в левую полуплоскость комплексной плоскости. В качестве примера рассмотрим, что получится, если синтезировать всего лишь устойчивый наблюдатель и использовать его для решения задачи стабилизации.

Построим матрицу усиления наблюдателя так, чтобы сдвинуть собственное число 4 в точку −2. Для этого, как и ранее, построим преобразование , приводящее матрицу к блочному нижнетреугольному виду. Нетрудно видеть, что в рассматриваемом случае матрица совпадает с найденной ранее, поэтому, применяя преобразование к матрицам , и получаем:

46

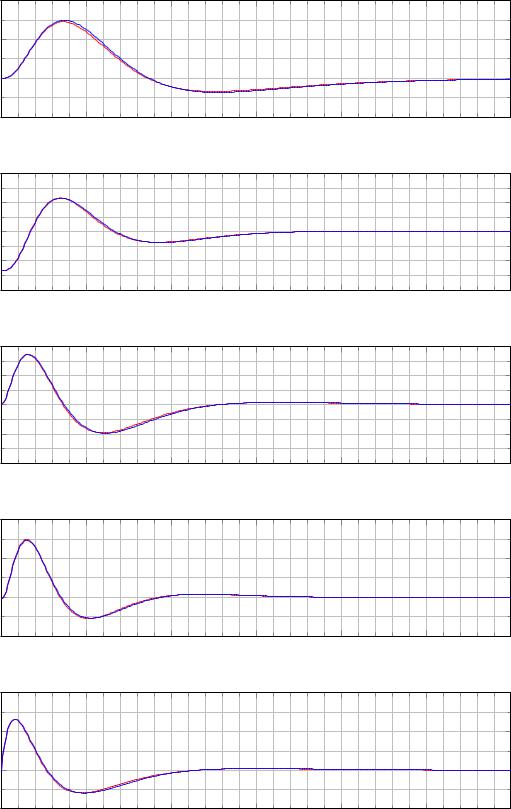
На рисунках 2.9 приведены графики переходных процессов в линейной (2.7) и нелинейной (2.4) системах, замкнутых регулятором (2.12) и наблюдателем (2.25). В качестве начальных условий была выбрана точка

0 = 0, −0.2, 0, 0 .

2.3. Дискретные системы управления 2.3.1. Дискретизация и восстановление сигналов

В предыдущих разделах при синтезе управления мы считали, что состояние объекта или его измеряемый выход изменяются непрерывно во времени и могут принимать любые конечные значения. Однако современные системы управления, как правило, реализуются с помощью компьютера, который способен хранить и обрабатывать только дискретную информацию. Таким образом, возникает необходимость преобразования непрерывных сигналов, поступающих с датчиков на вход компьютера, в дискретные (цифровые). Соответствующее устройство называется аналого-цифровым преобразователем (АЦП, analog-to-digital converter, A/D). Дискретные (цифровые) сигналы, получающиеся на выходе компьютера, в свою очередь, необходимо преобразовать обратно в непрерывные, чтобы использовать их в дальнейшем для управления объектом. За такое преобразование отвечает цифро-аналоговый преоб-

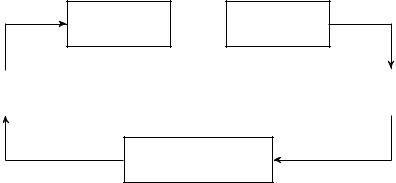
разователь (ЦАП, digital-to-analog converter, D/A). Схема соответствую-

щей системы управления изображена на рис. 2.10. Компьютер в этой системе выполняет функцию регулятора.

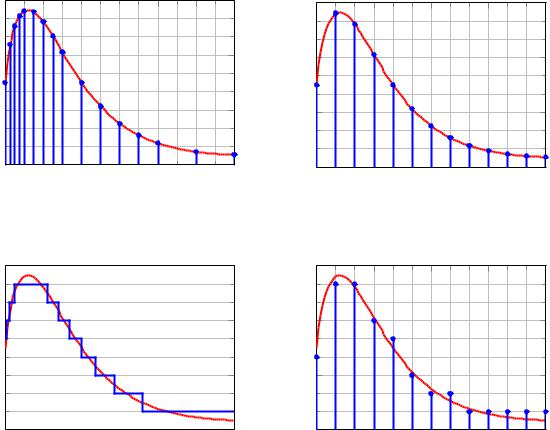
Преобразование непрерывного сигнала в дискретный называется квантованием или дискретизацией. Квантование возможно по времени, амплитуде, а также по времени и амплитуде одновременно. В случае квантования по времени непрерывный сигнал ( ) заменяется последовательностью значений ( ), взятых в произвольные дискретные моменты времени , + (рис. 2.11а). Получающийся таким образом дискретный сигнал называется импульсным. Очевидно, что такое преобразование приводит к потере информации о поведении исходного сигнала в промежутках между выбранными моментами. Для уменьшения ошибки квантования следует выбирать моменты дискретизации в за-

47

48

Рис. 2.11. Квантование непрерывного сигнала: (а) по времени в произвольные дискретные моменты ; (б) по времени с интервалом дискретизации ; (в) по амплитуде (уровню); (г) одновременно по времени и амплитуде.

получающийся при этом сигнал называется цифровым. Преобразование дискретного сигнала ( , ) + в непрерыв-

ный ( ) основано на аппроксимации функции ( ) некоторым полиномом, значения которого совпадают с в моменты времени , +. На практике чаще всего используются интерполяционные полиномы нулевого порядка. В этом случае значение непрерывного сигнала между моментами отсчёта сохраняется постоянным:

Устройство, восстанавливающее сигнал с помощью полинома нулево-

го порядка, называется эктраполятором нулевого порядка (Zero-Order Hold, ZOH).

Помимо полиномов нулевого порядка для восстановления непрерыв-

50