Методическое пособие 659

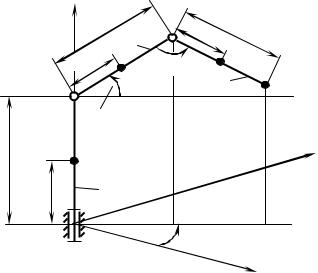
Обобщенными координатами являются углы 1, 2 и длина стрелы r. Взаимосвязь движений по координатам про-

является в наличии функциональных параметров A 1(r, 2), A 2(r) матрицы A(q), коэффициентов матрицы B(q,q), зави-

сящих от координат и их производных, а также функциональных параметров в матрице C(q) вследствие изменения потен-

циальной энергии при движении по координатам 2, r.

1.6.Уравнения движения манипулятора

вугловой системе координат

Расчетная схема манипулятора, работающего в угловой системе координат, приведена на рис. 1.4. Звено 1 имеет массу m1 и момент инерции J1 относительно оси вращения Оx2. Через m2, m3 и m обозначены, соответственно, массы звеньев 2, 3 и рабочего органа. Рассматриваемый манипулятор имеет три вращательные кинематические пары. Обобщенными коорди-

натами являются углы поворота 1, 2, 3.

l01 1

Рис. 1.4. Расчетная схема трехкоординатного манипулятора в угловых координатах

20

Уравнения Лагранжа для рассматриваемого трехкоординатного манипулятора имеют вид

где M j – моменты, развиваемые электроприводами в сочленениях вращательного типа.

Звено 1 участвует только во вращательном движении по

координате 1, поэтому его кинетическая энергия определяется из выражения

Звенья 2 и 3 совершают сложные движения. Обозначим через V2, V3 и V значения скоростей точек, в которых сосредоточены массы m2, m3 и m. Тогда для определения кинетической энергии звеньев 2, 3 и груза m запишем следующие выражения:

s 1

Квадрат скорости точки m2 определяется из выражения, аналогичного (1.37):

(1.54)

Координаты xs3 точки m3 определяются из выражений: x13 [l2 cos 2 l03 cos( 2 3)] sin 1 ,

21

[l2 cos 2 l03 cos( 2 3)] sin 1 1.

Квадрат скорости точки m3 равен

Подставляя в (1.57) выражения для определения скоростей x13, x23 и x33 из (1.56), после ряда тригонометрических преобразований получим следующее уравнение:

Аналогичным образом выводится выражение для квадрата скорости точки m, имеющее следующий вид:

Кинетическая энергия W системы определяется из выражения

На основе уравнений (1.52)–(1.54), (1.58)–(1.60) получим следующее выражение:

W( 2, 3, 1 , 2 , 3 ) = J1 12 / 2 + m2 l022( 12 cos2 2 + 22 ) /2 + + m3{l22[ 22 + cos2 2 12 ]+l032[( 2 + 3 )2 + cos2( 2+ 3) 12 ] –

–2l2l03[cos 3 2 ( 2 + 3 ) + cos 2 cos( 2+ 3) 12 ]}/2 +

+m{l22[ 22 + cos2 2 12 ] + l32[( 2 + 3 )2 + cos2( 2+ 3) 12 ] –

22

Частные производные от кинетической энергии по производным от обобщенных координат равны

Выражение для потенциальной энергии П системы имеет вид

П( 2, 3)=m1gl01+m2g(l1+l02sin 2)+m3g(l1+l2sin 2 –

–l03 sin ( 2+ 3)]+mg[l1+l2sin 2 – l3sin ( 2 + 3)]. (1.64)

Производные от П( 2, 3) по обобщенным координатам:

Подставляя в систему (1.51) выражения для частных производных (1.62), (1.63) и (1.65), после проведения операции дифференцирования по времени и выполнения ряда тригонометрических преобразований получим следующие уравнения динамики манипулятора в угловой системе координат:

23

1[J1 (m2l022 ml22 m3l22)cos2 2 (m3l032 ml32)

cos2( 2 3) 2l2(m3l03 ml3)cos 2 cos( 2 3)]

1{ (m2l022 ml22 m3l22)sin2 2 2 (m3l032 ml32)

sin[2( 2 3)]( 2 3) 2l2(m3l03 ml3)[sin(2 2 3) 2

cos 2 sin( 2 3) 3]} M 1,

sin( 2 3)} 22(m3l03 ml3)l2 sin 3 g(m3l03 ml3)

cos( 2 3) M 3.

Введем следующие обозначения:

A 1( 2, 3) J1 (m2l022 ml22 m3l22)cos2 2 (m3l032 ml32)

cos2( 2 3) 2l2(m3l03 ml3)cos 2 cos( 2 3),

B 1( 2, 3, 1, 2, 3) 1{ (m2l022 ml22 m3l22)sin2 2 2

(m3l032 ml32)sin[2( 2 3)]( 2 3) 2l2(m3l03 ml3)

[sin(2 2 3) 2 cos 2 sin( 2 3) 3},

24

С учетом (1.67) уравнения динамики манипулятора в угловой системе координат приобретают следующий вид:

Векторная форма записи системы уравнений (1.68) имеет вид выражения (1.30), в котором матрицы A(q), q , P,

B(q,q) и C(q) определяются следующим образом:

Обобщенными координатами являются углы 1, 2, 3.

25

В отличие от рассмотренных ранее кинематических схем и, в частности, от схемы манипулятора, работающего в сферической системе координат, динамика которого также характеризуется наличием функциональных коэффициентов в матрице A(q), векторах B(q,q) и C(q), для данной схемы матрица

инерции A(q) не является диагональной, что свидетельствует о

влиянии ускорения по координате 2 на движение по 3, и наоборот.

Следует отметить, что независимо от кинематической схемы манипулятора его динамическая модель всегда может быть представлена в виде уравнения (1.30). На основе этого векторного уравнения строятся алгоритмы управления манипуляторами. На синтез управления также оказывают влияние модели электроприводов в сочленениях робота.

В связи с этим рассмотрим далее модели двух типов электроприводов, широко применяющихся для реализации сложных движений манипуляторов, – постоянного тока и асинхронного.

1.7. Динамические модели электроприводов промышленных роботов

Широкое распространение в регулируемых электроприводах роботов получили двигатели постоянного тока благодаря хорошим регулировочным свойствам и простоте системы управления ими. Как правило, двигатели постоянного тока управляют изменением подводимого к якорю напряжения при постоянном магнитном потоке машины. Дифференциальные уравнения, описывающие такую систему, имеют следующий вид:

где Lj – индуктивность цепи якоря двигателя j-й координаты; Ij – ток якоря двигателя j-й координаты;

26

Rj – активное сопротивление цепи якоря двигателя j-й координаты;

kej – коэффициент противоЭДС двигателя j-й координаты; qдj – угол поворота вала двигателя j-й координаты;

Uj – напряжение на якоре двигателя j-й координаты; kmj – коэффициент момента двигателя j-й координаты;

J j – момент инерции якоря двигателя j-й координаты;

kтр – коэффициент вязкого трения;

Mнj – момент внешней нагрузки, приведенный к валу двигателя j-й координаты.

Первое уравнение системы (1.70) описывает электромагнитные процессы, происходящие в цепи якоря двигателя. Второе уравнение связывает электромагнитный момент двигателя, динамический момент, момент вязкого трения и момент нагрузки на валу, т. е. является основным уравнением движения электропривода j-й координаты.

В настоящее время в роботах также применяется регулируемый асинхронный электропривод. Управляемость асинхронного электропривода обеспечивается путем одновременного регулирования частоты f1 и напряжения U1 или тока I1 статорной обмотки с помощью трехфазного преобразователя частоты.

Значительная часть используемых преобразователей частоты обладает свойствами трехфазного регулируемого источника тока, т. е. формирует в фазах двигателя токи, которые не зависят от режима работы и параметров двигателя, а определяются только сигналом задания.

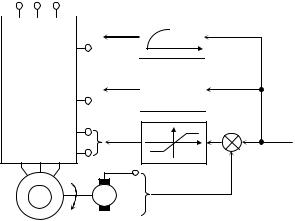
Функциональная схема системы воспроизведения момента при питании обмотки статора асинхронного двигателя токами регулируемой частоты, амплитуды и фазы показана на рис. 1.5. Схема содержит следующие элементы:

РИТ регулируемый источник тока; Μ асинхронный двигатель;

G тахогенератор;

НЗ1, НЗ2 нелинейные звенья; РМ регулятор момента.

27

R2 – приведенное активное сопротивление ротора;

2х, 2у – проекции вектора потокосцепления ротора 2 на оси x, y;

0эл,ном – электрическая угловая скорость поля двигателя при номинальной частоте f1ном токов статора;

sa=( 0эл– эл)/ 0эл,ном=( 0– )/ 0ном – абсолютное скольжение, равное отношению отклонения скорости ротора от

скорости 0 поля при текущей частоте f1 токов статора к скорости поля 0ном приноминальной частоте f1ном;

Подставляя соотношения (1.73) и значения производных

от потокосцеплений d 2x dt = 0, d 2y dt = 0 в уравнения динамики (1.71), получаем

29