Методическое пособие 659

Число параметров aj,s , подлежащих определению, равно 4m, а число условий пока равно 3m – 1: 2m условий непрерывности и приближения

и m – 1 условий непрерывности первой производной

Кроме этого, имеется m – 1 условий непрерывности ускорений

а также требуемые граничные условия.

Если никаких дополнительных условий на концах траектории не накладывается, то принимаются следующие граничные условия:

Однако необходимо учитывать практические потребности. Если движение начинается из состояния покоя и заканчивается состоянием покоя, то прежде всего необходимо потребовать наложения условий на начальную и конечную скорость

но тогда ограничение на ускорения (3.47) в общем случае не будет выполняться. Одновременное выполнение условий (3.47) и (3.48) в общем случае невозможно при использовании только кубических сплайнов: ограничений оказывается больше, чем определяемых параметров. Поэтому задачу решают с граничными условиями (3.48), а возникающие при этом ненулевые ускорения можно устранить путем добавления к перво-

70

му и последнему сплайнам специальных функций. Например, вместо Pj,13(t) и Pj,m3(t) можно взять на первом и последнем отрезках траектории многочлены пятого порядка

Эти функции не нарушают предыдущих ограничений, но обеспечивают также и выполнение условия (3.47).

Сплайн-функции задающих сигналов электроприводов строятся для каждой степени подвижности. Затем проверяется, правильно ли назначены продолжительность Т управления и разбиение этого интервала на отрезки [ts–1, ts]. Для этого нужно определить максимально допустимую скорость и, если это необходимо, максимальное ускорение каждой степени подвижности.

Первое приближение для узлов интерполяции ts определяется из формулы

ts = ts–1 + max(|qjs – qj,s–1|) / jmax ), t0 = 0, (3.51)

где j max – максимально допустимая скорость j-го привода. Если после построения кубических сплайнов на каком-

либо отрезке сплайн-функция имеет скорости и (или) ускорения, превосходящие допустимые, то такой отрезок соответственно увеличивается. Затем для нового интервала [0,T] и нового его разбиения на отрезки [ts–1, ts] повторяется построение сплайн-функций, т. е. задающие функции строятся методом последовательных приближений.

Формирование задающих сигналов занимает от десятых долей секунды до нескольких секунд в зависимости от мощности ЭВМ и используемого языка программирования. После этого задающие функции подаются в реальном масштабе времени на исполнительный уровень управления для реализации запланированного движения.

71

Контрольные вопросы

1.Какие типы управления различают при планировании движений робота?

2.Каким ограничением должно удовлетворять программное движение?

3.Перечислите условия, предъявляемые к базисным функциям, и поясните их смысл.

4.Приведите примеры рационального выбора базисных функций.

5.Каким правилом можно руководствоваться при конструировании базисных функций?

6.Поясните смысл условных и безусловных неравенств.

7.Приведите выражение и дайте определение конечносходящегося алгоритма решения условных и безусловных неравенств.

8.Какие условия должны быть выполнены для того, чтобы было обоснованным применение конечно-сходящегося

алгоритма «Полоска-1»

9.Приведите выражения и поясните геометрический смысл конечно-сходящегося алгоритма «Полоска-1».

10.Каким образом осуществляется построение про-

граммных движений тележки мобильного робота

11.Каким образом осуществляется построение программных движений манипулятора

12.Дайте определение и поясните назначение сплайна

порядка .

13.Изобразите виды сплайнов при различных значениях порядка .

14.Какие преимущества имеет интерполяция траектории кубическими сплайнами?

15.Какие существуют ограничения на параметры движения вдоль заданной траектории?

16.Как определяются длительности временных интервалов между опорными точками при интерполяции траектории?

72

4. ДИНАМИЧЕСКОЕ УПРАВЛЕНИЕ МАНИПУЛЯТОРАМИ

В предыдущей главе рассматривались уравнения кинематики и построенные на их основе кинематические алгоритмы управления. Настоящая глава посвящена синтезу управления с учетом динамики манипулятора (динамическому управлению). При этом рассматриваются алгоритмы позиционного, контурного и силового управления.

4.1. Методы управления, основанные на решении обратной задачи динамики

Обратная задача динамики состоит в определении век-

тора обобщенных сил P(t), который необходим для отработки системой управления векторов заданных траекторий qзад(t) обобщенных координат, их первых q зад(t) и вторых q зад(t)

производных.

В методах управления, основанных на решении обратной задачи, математическая модель динамики манипулятора непосредственно включается в систему управления. Так, в работе [3] описаны подходы, предусматривающие формирование полной динамики робота в процессе управления, т. е. вычисление обобщенных сил в соответствии с уравнением (1.30) при использовании измеренных значений обобщенных координат q(t) и скоростей q(t) робота. Было показано, что робот

является асимптотически устойчивым в окрестности номинальной траектории, если вектор обобщенных сил вычисляется следующим образом [3]:

P(t) = A(q(t)){ qзад(t) + K0[qзад (t) – q(t)] +

где K0 – матрица размером n n коэффициентов обратной связи по положению;

K1 – матрица размером n n коэффициентов обратной связи по скорости.

73

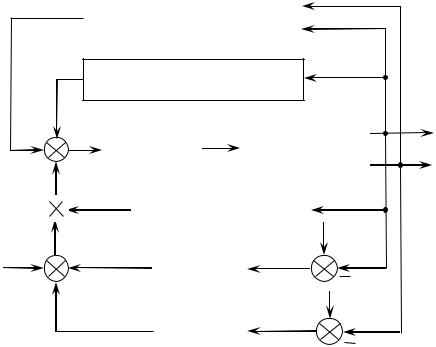
Схема системы управления, построенной в соответствии с методом «обратной задачи», показана на рис. 4.1. Схема вычисляет вектор P(t) обобщенных сил в соответствии с уравнением (4.1); вектор U(t) управляющих сигналов рассчитывается на основе уравнений динамики исполнительных приводов.

В схеме учитываются взаимовлияние звеньев [матрица B(q,q)], гравитационные силы [матрица C(q)], изменение мо-

ментов инерции при движении манипулятора [в матрице A(q)].

Рис. 4.1. Схема системы управления по методу «обратной задачи»

Данный подход обладает рядом недостатков. Основная проблема состоит в том, что при вычислении по формуле (4.1) требуется полная модель динамики манипулятора робота. Как

74

было показано в гл. 1, математическая модель механической части манипулятора даже для относительно простых трехкоординатных расчетных схем, работающих в цилиндрической, сферической и угловой системах координат, представляет собой сложную систему взаимосвязанных нелинейных дифференциальных уравнений.

Для робота со сложной манипуляционной системой расчет управлений в реальном времени может оказаться нецелесообразным или даже невозможным. В связи с этим известны многочисленные попытки применять упрощенные модели динамики манипуляторов, в которых для облегчения вычислений опущены некоторые составляющие модели.

Обычно в (1.30) пренебрегают компонентой B(q,q ), т. к.

она несущественна в окрестности целевого положения (значения скоростей сочленений в это время малы). Пренебрегают также взаимовлиянием моментов инерции в матрице A(q). Это означает, что модель упрощается до диагональных элементов матрицы A(q) и до гравитационных сил, т. е. управление (4.1) сводится к выражению

где Ajj(q(t)) – диагональная матрица инерционных параметров.

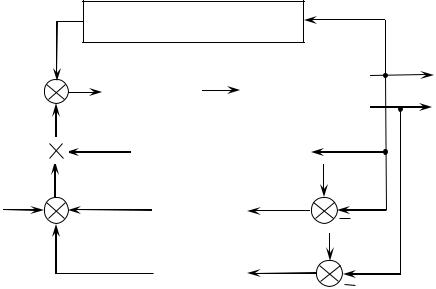
Схема системы управления в этом случае имеет вид, приведенный на рис. 4.2.

Благодаря принятым упрощениям вычисления значительно сокращаются, но для некоторых типов манипуляторов они остаются громоздкими. С другой стороны, возникает вопрос: не снижают ли эти упрощения эффективность управления?

Предположение об отсутствии взаимовлияния звеньев полностью оправдано для манипулятора, работающего в декартовой системе координат (1.16), для трехкоординатных манипуляторов с декартовой, цилиндрической и угловой си-

75

стемами координат матрица A(q) является диагональной (1.17), (1.31), (1.50). В общем случае применение упрощенных выражений должно быть обосновано исходя из конкретных требований к динамике проектируемой системы; на практике необходимо искать разумный компромисс между сложностью управляющей техники и качеством исполнения роботом заданий.

Рис. 4.2. Схема системы управления по методу «обратной задачи» c упрощенными вычислениями

Таким образом, с методом «обратной задачи» связано несколько проблем, которые определяются сложностью его реализации и трудностью использования. Кроме того, до сих пор не разработана систематическая процедура для синтеза управления произвольным манипулятором (выбор сложности модели, структуры и коэффициентов матриц K0, K1 обратной связи и т. д.).

76

Основная проблема, связанная с рассмотренными схемами управления, заключается во включении динамической модели манипулятора непосредственно в структуру управляющей системы, что делает исполнение подобных схем сложным и непрактичным. К тому же, реализация законов управления (4.1) или (4.2) требует знания всех параметров манипулятора, входящих в матрицы A(q), B(q,q ) и C(q).

Однако в общем случае параметры механизма заранее не известны. Поэтому, несмотря на сложность вычислений, управление (4.1), реализованное для фиксированных параметров механизма, не гарантирует достижения заданной цели управления.

В работе [5] изложены основы синтеза алгоритмов исполнительного уровня управления на базе принципа управления по ускорению. Эти алгоритмы придают проектируемым системам естественные свойства адаптивности, слабой чувствительности к изменению параметров манипулятора и координатных возмущений, что исключает необходимость иметь полную информацию о математических моделях управляемого движения.

Структура алгоритмов соответствует исходным нелинейным уравнениям манипулятора, т. к. параметры рассчитываются на основе концепций обратных задач динамики из условия реализации назначаемых динамических характеристик. В то же время матрицы A(q), B(q, q ) и C(q) не рассчи-

тываются в ходе формирования управляющих воздействий, что значительно сокращает время вычислительных операций. Поэтому алгоритмы управления по ускорению представляют большой практический интерес.

4.2.Алгоритмы управления по ускорению

Вэтом разделе рассмотрим задачу синтеза алгоритмов управления по ускорению пространственным движением исполнительных механизмов (манипуляторов) роботов.

77

На основе выражений (1.30) и (1.70) составим следующую систему уравнений динамики манипулятора с исполнительными приводами постоянного тока:

где Мдj – электромагнитный момент исполнительного двигателя j-й координаты.

Для вращательных степеней подвижности, учитывая коэффициент передачи редуктора nj, преобразуем уравнения динамики привода постоянного тока следующим образом:

обобщенной координаты;

Pj – обобщенная сила, представляющая собой для вращательного движения момент в j-м сочленении механизма.

Представим систему (4.4) в следующем виде:

Tэj Mд j + Мдj = Uj kmj /Rj – kmjkejnj qj /Rj,

где Мсj( qj ) – момент сопротивления на валу двигателя j-й

координаты от сил вязкого трения;

Тэj=Lj/Rj – электрическая постоянная времени двигателя j-й координаты.

В векторной форме система (4.5) запишется в виде

78

В уравнениях системы (4.6) приняты следующие обозначения:

где ~ ( ) = ( ) + – матрица размера .

А q A q O n n

В современных электродвигателях, используемых в конструкциях манипуляторов, электрические постоянные времени существенно меньше электромеханических постоянных времени, т. е.

В таких случаях можно принять Тэj = 0. Это позволяет вместо (4.9) рассматривать уравнения

79