1.3. Дифференциальные уравнения с

РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

. (1.8)

Будем предполагать, что функции непрерывны в интервалах и соответственно, и пусть при . Умножив ОДУ (1) на , получим уравнение

, (1.9)

в котором левая и правая части зависят от разных переменных. Преобразование уравнения (1.8) к виду (1.9), называется разделением переменных. Интегрируя левую и правую части (1.9) приходим к равенству

. (1.10)

Вычисление неопределенных интегралов в (1.10) приводит к общему интегралу ОДУ (1.8).

При переходе к равенству (1.9) предполагалось, что . Если это условие нарушено, то из (1.8) непосредственно следует, что все значения , для которых , дают дополнительные решения ОДУ (1.8) вида .

Замечание. Уравнение с разделяющимися переменными может быть задано в виде

Тогда делением на произведение оно приводится к уравнению с разделенными переменными

.

Общий интеграл полученного уравнения находится почленным интегрированием

.

Уравнению могут удовлетворять решения, потерянные при делении на , т.е. получаемые из уравнения =0.

Задача 1.4. Шарик, масса которого , нанизан на горизонтальную проволочную круговую петлю радиуса (рис.3). Зная коэффициент трения , определить, какую начальную скорость нужно сообщить шарику для того, чтобы он сделал полный оборот по проволоке и остановился.

Решение. На шарик действуют четыре силы (рис.3): сила тяжести Р с абсолютным значением - ускорение свободного падения), центробежная сила N инерции с абсолютным значением ( - скорость шарика), сила N реакции проволоки и направленная против его движения сила F трения. Реакция проволоки уравновешивает силу тяжести и центробежную силу инерции, т.е. абсолютное значение силы N

Тогда абсолютное значение силы трения

Согласно второму закону Ньютона, запишем уравнение движения шарика в виде

Поскольку , где - расстояние, пройденное шариком

после начала движения, то можно записать

В итоге получаем уравнение движения шарика в виде

Это ОДУ с разделяющимися переменными. После разделения переменных и интегрирования находим

Интеграл в левой части этого равенства подстановкой можно свести к табличному интегралу, так что приходим к соотношению

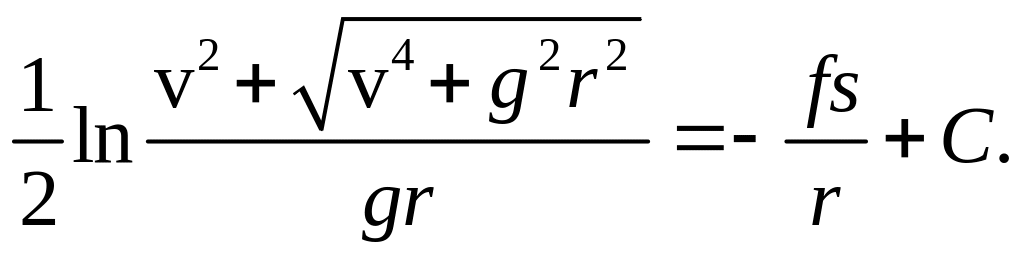
По условию, при . Отсюда . Начальную скорость шарика найдем из условия при , т.е.

или (после решения биквадратного уравнения относительно

) Характерно, что значение и движение шарика не зависит от его массы.

Задача 1.5. Решить уравнение Найти интегральную кривую, проходящую через точку

Решение. Запишем данное уравнение в виде: или . Полученное уравнение является уравнением с разделенными переменными (коэффициент при - функция только от , при - функция только от ).

Интегрируя, получим или . Полагая (что можно сделать, так как ,общий интеграл запишем в виде Геометрически общий интеграл представляет собой семейство окружностей радиусов с центром в начале координат.

Найдем ту окружность, которая проходит через точку Подставляя координаты точки в уравнение , находим или . Подставив значение в общий интеграл, получим искомую окружность

Задача 1.6. Решить дифференциальное уравнение

Решение. Перепишем исходное уравнение в виде

. Поскольку и ,

разделяем переменные, т.е. представляем уравнение в виде

Интегрируем левую и правую части уравнения:

,

Получим . Упростив это равенство, получим - решение уравнения.

Задача 1.7. Найти частное решение уравнения

Решение. Разделяя переменные и интегрируя, находим общее решение заданного уравнения:

, ,

откуда , т.е. , или (положили . Подставляя в найденное общее решение и (используем начальное условие), находим постоянную . А именно: Следовательно, искомое частное решение имеет вид: