1.2.2. Вычисление ранга матриц

Определение 1. Максимальное число линейно независимых столбцов (строк) матрицы называется рангом этой матрицы и обозначается .

Теорема 1. Наивысший порядок отличных от нуля миноров матрицы равен рангу этой матрицы.

Правило вычисления ранга матрицы. При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор k-го порядка , отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор . Если все они равны нулю, то ранг матрицы равен . Говорят, что минор окаймляет минор D, если D содержится внутри , другими словами, столбцы и строки, образующие D, входят в множество столбцов и строк, образующих .

Определение 2. Под элементарным преобразованием строк (столбцов) матрицы А понимаются:

а) перестановка местами двух строк (столбцов);

б) умножение строки (столбца) на любое число, неравное нулю;

в) сложение любой строки (столбца) с другой строкой (столбцом), умноженной на некоторое число.

Теорема 2. Элементарные преобразования строк (столбцов) матрицы не меняют ранга этой матрицы.

Упражнение 1. Пусть

.

Показать, что

Упражнение 2. Пусть матрица размерности , имеющая ранг 1. Доказать, что найдутся матрицы размерностей и соответственно такие, что

.

Решение. Так как ранг матрицы равен 1, то все ее строки пропорциональны одной (скажем, первой). Тогда

.

Осталось положить .

Упражнение 3. Пусть квадратная матрица А порядка и . Найти ранг присоединенной матрицы где алгебраическое дополнение элемента матрицы .

Решение. 1) если , то . Значит, ;

2) если то все миноры (n–1)-го порядка равны 0. Следовательно, нулевая матрица и ее ранг равен нулю;

3) если то запишем в виде _– в виде , где вектор-столбцы, состоящие из n элементов. Обозначим множество (пространство) всевозможных линейных комбинаций векторов символом . Под размерностью пространства понимается количество векторов, образующих базис этого пространства, и обозначается . Так как , то . Так как , только если для всех , то . Это означает, что выполнено равенство .

Задачи для самостоятельного решения

1. Вычислить определители приведением к треугольному виду:

а) , б) ,

в) , г)

2. Вычислить определители методом рекуррентных соотношений:

а) , б) ,

в) , г)

д) е)

3. Рядом Фибоначчи называется числовой ряд, который начинается числами 1, 2 и в котором каждое следующее число равно сумме двух предыдущих, то есть, 1, 2, 3, 5, 8, 13, 21, … .

Доказать, что -й член ряда Фибоначчи равен следующему определителю -го порядка:

.

4. Вычислить определители методом разложения на линейные множители:

а) , б) ,

в) , г)

5. Используя теорему Лапласа, вычислить определители:

а) , б) , в) .

6. Вычислить определители, представляя их в виде произведения определителей:

а) ,

б) ,

в) .

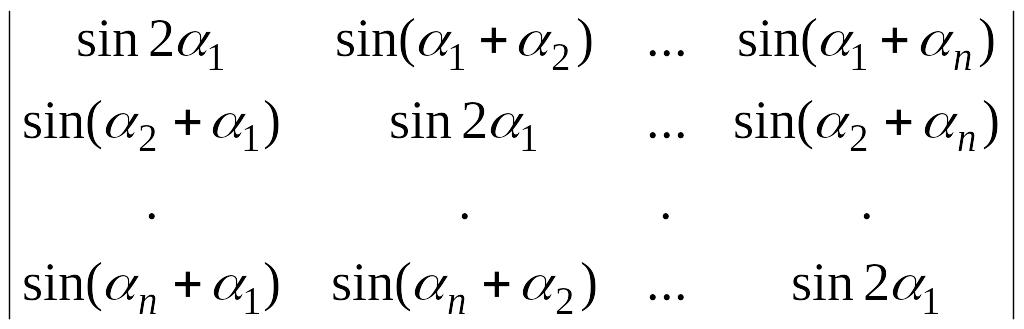7. Показать, что если , то

.

8. Доказать, что определитель матрицы , где – произвольная квадратная матрица, равен нулю.

9. Доказать, что из следует равенство , где – квадратные матрицы одного порядка.

10. Вычислить определитель посредством умножения его на определитель .

а) , ;

б) , .

11. Пусть – квадратные матрицы одного порядка. Доказать, что

.

12. Доказать, что ранг произведения двух матриц не превосходит ранга каждой из матриц-сомножителей.

13. Доказать, что приписывание к матрице одной строки (одного столбца) либо не изменяет ранга этой матрицы, либо увеличивает его на единицу.

14. Доказать, что любую матрицу ранга можно представить в виде суммы матриц ранга единица.

Указание. Элементарными преобразованиями привести исходную матрицу к матрице, содержащей ровно ненулевых элементов, и представить последнюю в виде суммы матриц, каждая из которых имеет единственный нулевой элемент.