8. Дифференциалы высших порядков. Формула Тейлора

Дифференциалом второго порядка d²f(x) функции называется дифференциал от дифференциала , где рассматривается как функция от x: d²f = d(df) .

Дифференциалом третьего порядка d³f называется дифференциал от второго дифференциала: d³f = d(d²f); и т.д.

Если переменная x является независимой, то d²x = d³x = … = 0. В этом случае , ,..., ,… Для краткости вместо (dx)ⁿ принято писать dxⁿ; с учётом этого .

Если функция определена в некоторой окрестности точки x₀ и в этой окрестности имеет производные до (n+1) -го порядка включительно (т.е. дифференцируема (n+1) раз), то справедлива формула Тейлора

,

где R_n+1 (x) – остаточный член, являющийся бесконечно малой величиной при x  x₀. Остаточный член обычно записывают в виде в форме Пеано или в форме Лагранжа , где с – некоторое число между x₀ и x. Формула Тейлора допускает и другую запись через дифференциалы

.

Формулу Тейлора применяют для приближенных вычислений.

Пример 10. С помощью формулы Тейлора найти приближённое значение sin 1 с точностью до 0,001.

Решение. Введём в рассмотрение функцию . Положив x₀ = 0, получим

,

где 0 < c < 1 (формула Тейлора с остаточным членом в форме Лагранжа).

Имеем , , , , , …, . Для вычисления требуемого значения нужно взять n таким, чтобы , или

; .

Это неравенство достигается при n = 6 , т.к.7  = 5040 >1000. Поэтому .

9. Раскрытие неопределённостей по правилу Лопиталя

Теорема. Пусть функции f(x) и g(x) определены и дифференцируемы в каждой точке некоторой окрестности точки x₀, кроме, может быть, самой точки x₀, и пусть . Если =0 или и существует , то .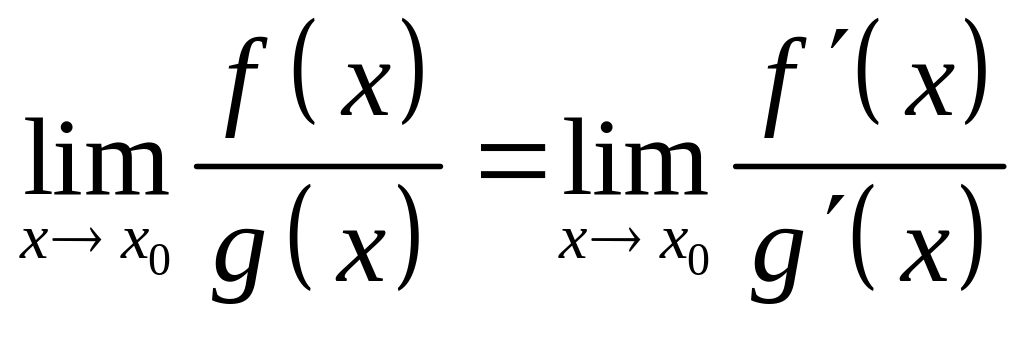

Эта теорема, называемая правилом Лопиталя, применяется для раскрытия неопределённостей вида или .

Неопределённости вида или несложным алгебраическим преобразованием приводятся к неопределённостям вида или .

Неопределённости вида приводятся к неопределённости вида с помощью предварительного логарифмирования или тождества .

Пример 11. Применяя правило Лопиталя, найти пределы:

а) ; б) ; в) ; г) ;

д) .

Решение.  а) Первый способ. При x1 числитель и знаменатель стремятся к 0, поэтому имеем неопределённость вида . Воспользуемся правилом Лопиталя:

Второй способ. Неопределённость можно раскрыть и с помощью формулы Тейлора. Обозначим , . Эти функции определены и дифференцируемы в окрестности точки x₀ = 1. Имеем , , , , , . Согласно формуле Тейлора с остаточным членом в форме Пеано,

,

Или , .

Поэтому

.

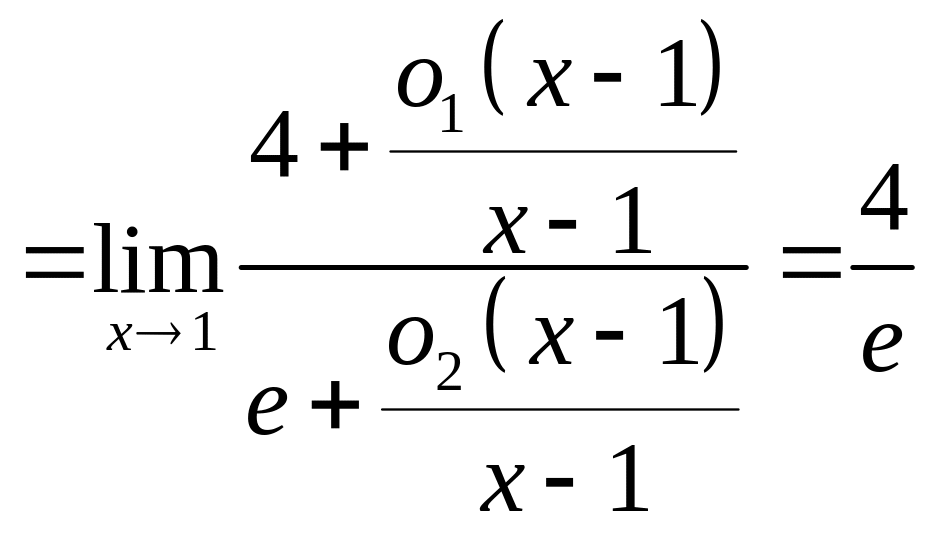б) Здесь мы имеем неопределённость вида . В данном случае приходится трижды применять правило Лопиталя:

.

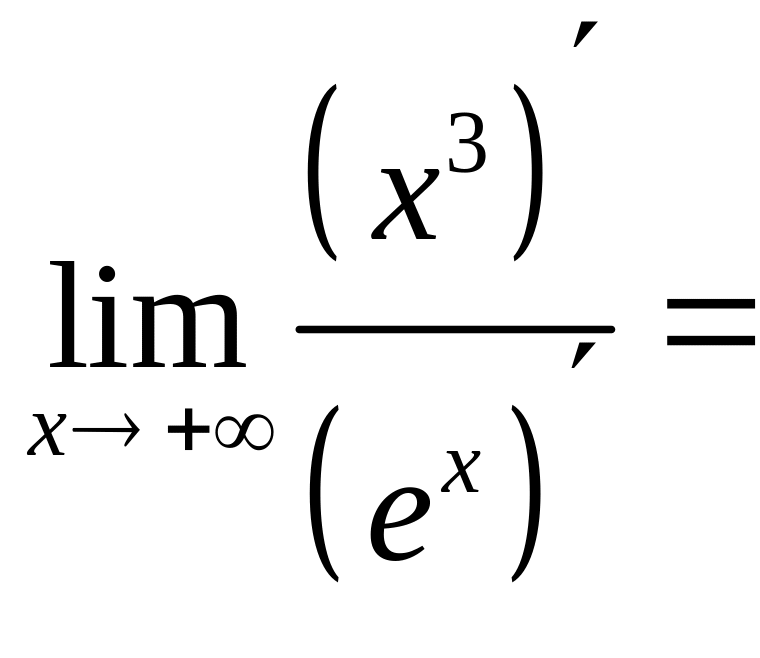
в) Имеем неопределённость вида . Обозначим . Тогда ,

.Таким образом, , откуда, ввиду непрерывности логарифмической функции, ,то есть .

г) Воспользуемся тождеством , 0 < x < /2. Ввиду непрерывности показательной функции

Найдем :

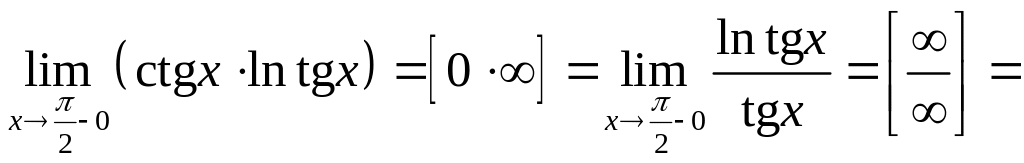
Итак, .

д) Имеем неопределённость вида . Переведём эту неопределённость в неопределённость вида и затем воспользуемся правилом Лопиталя:

.

А так как

,

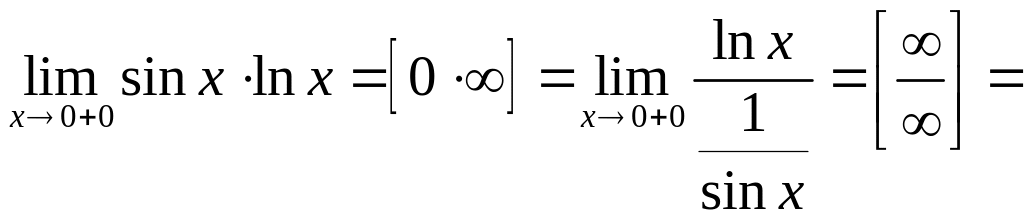
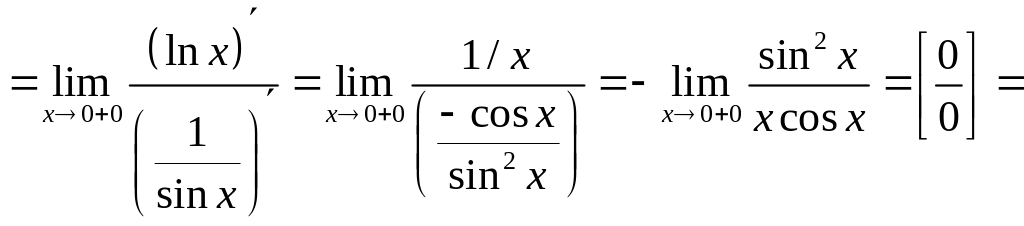
то .