7.3. Математический маятник

Математическим маятником будем называть всякую систему, состоящую из тела подвешенного на нерастяжимой нити или невесомом стержне и способного совершать колебания около положения равновесия, причем линейные размеры тела должны быть много меньше длины нити .

Рис. 49

По определению момента сил, в данном случае момент силы тяжести:

, (7.23)

С другой стороны, согласно основному уравнению динамики вращательного движения:

(7.24)

Приравнивая правые части (7.23) и (7.24), получим:

, (7.25)

, (7.26)

. (7.27)

При малых колебаниях , отсюда, введя обозначение , (можно проверить, что размерность совпадает с размерностью ) получим:

. (7.28)

Период колебаний математического маятника:

. (7.29)

7.4. Физический маятник

Физическим маятником будем называть всякое тело подвешенное в точке, не совпадающей с центром тяжести тела.

Рис. 50

Проделав шаги, аналогичные тем, что были в примере математического маятника, получим:

В случае малых колебаний:

где, (также можно доказать равенство размерностей величин, стоящих в обоих частях данного равенства).

(7.30)

Таким образом, математический маятник с длиной будет иметь тот же период колебаний, что и для математического маятника.

Центр качания - точка на прямой, соединяющей центр подвеса и центр инерции на расстоянии ( носит название приведенной длины физического маятника) от оси вращения.

7.5. Энергия гармонических колебаний

(7.31)

(7.32)

Потенциальная энергия в точке будет частично равна работе квазиупругой силы, совершенной при перемещении из положения равновесия в данную точку и взятой с обратным знаком. Поэтому:

(7.33)

(7.34)

Полная энергия:

(7.35)

7.6. Затухающие колебания

В реальных условиях при рассмотрении колебаний нельзя не учитывать действие сил трения. При малых скоростях движения сопротивление обычно пропорционально первой степени скорости и направлено противоположно ей, т.е.:

(7.36)

С учетом этого дифференциальное уравнение движения материальной точки под действием квазиупругой силы и силы трения примет вид:

(7.37)

С точки зрения высшей математики мы получили однородное дифференциальное уравнение второго прядка, решение которого находится в виде:

. (7.38)

Первая и вторая производная от получившегося решения равны соответственно:

(7.39)

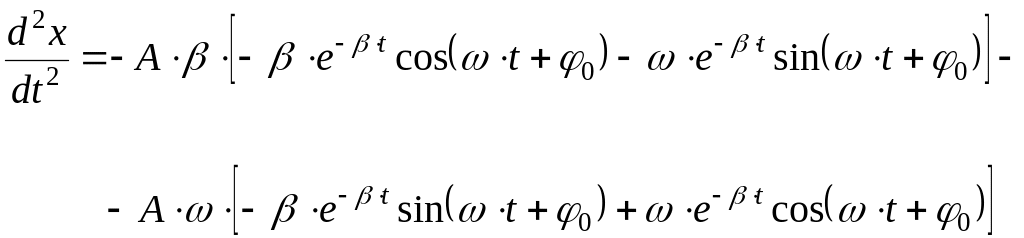(7.40)

Подставив , , в исходное дифференциальное уравнение (7.37), получим:

Сократим обе части на и сгруппируем полученные слагаемые:

Данное равенство выполняется при условии:

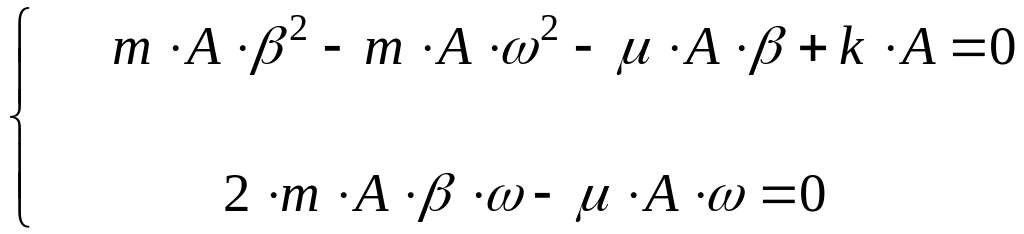(7.41)

Из второго уравнения следует, что коэффициент затухания

. (7.42)

Тогда, рассматривая первое выражение системы (7.41), получим:

Или:

,

,

,

,

. (7.43)

Общее решение дифференциального уравнения затухающих колебаний отличается от чисто гармонического колебания тем, что амплитуда колебания является убывающей функцией времени.

Рис.51

Чем больше , тем больше величина , а, следовательно, меньше амплитуда затухающих колебаний. Если трением пренебречь и положить , тогда и станет равным нулю, то мы придем к случаю обычных гармонических незатухающих колебаний с некоторой постоянной угловой частотой

Как видно из полученного решения дифференциального уравнений затухающих колебаний, при наличии силы трения не только амплитуда убывает со временем, но и уменьшается угловая частота колебаний по закону , где - угловая частота собственных колебаний точки при отсутствии трения.

Период затухающих колебаний равен:

. (7.44)

С увеличением трения период колебаний возрастает и в пределе при становится бесконечно большим. При дальнейшем увеличении движение становится апериодическим.

Амплитуда затухающих колебаний за каждый период убывает в одно и то же число раз:

(7.45)

Прологарифмировав обе части равенства, получим:

- логарифмический декремент затухания.

Величина носит название добротности.