Затухающие движения

Рассмотрим случай, когда (случай большого сопротивления). Корни характеристического уравнения в этом случае имеют значения

,

где введено новое обозначение для положительной величины .

Оба корня характеристического уравнения действительны и отрицательны, так как . Следовательно, общее решение дифференциального уравнения имеет вид

, (35)

г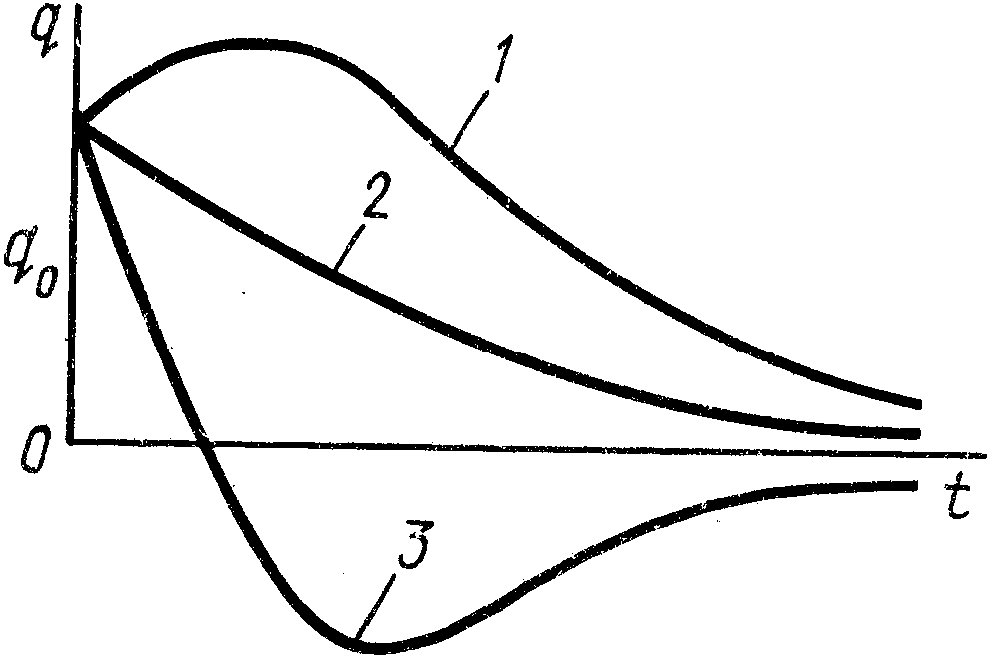 де и - произвольные постоянные, которые можно определить по начальным условиям

; ; .

Н

Рис. 8

е выполняя этих вычислений, можно оценить поведение функции , используя уравнение (35). Для могут представится три случая в зависимости от знака и значения (рис. 8).

При функция некоторое время возрастает до определенного максимума, а затем убывает, асимптотически приближаясь к нулю, так как вследствие того, что показатели степеней и отрицательны (кривая 1).

При неочень больших по абсолютной величине отрицательных значениях может сразу начаться убывание (кривая 2). При больших по модулю отрицательных значениях функция , убывая, может достичь нулевого значения, соответствующего положению равновесия системы, стать отрицательной и, оставаясь отрицательной, асимптотически приближаться к нулю (кривая 3). Во всех этих случаях движение является затухающим, неколебательным, которое иногда называют также апериодическим.

При (случай критического сопротивления) характеристическое уравнение имеет кратный отрицательный корень

.

Соответственно этому решение дифференциального уравнения имеет вид

. (36)

Произвольные постоянные и определяются по начальным условиям. В этом случае при , стремящемся к бесконечности, стремится к нулю при любых конечных значениях постоянных и , так как

,

что проверяется раскрытием неопределенности по правилу Лопиталя.

Таким образом, случай критического сопротивления тоже дает затухающее движение.

При движение не является колебательным и с некоторого момента времени начинается так называемое лимитационное движение, при котором система асимптотически стремится вернуться к положению равновесия.

Анализ влияния линейного сопротивления на собственные малые колебания показывает, что линейное сопротивление не может сделать устойчивое положение равновесия неустойчивым. Если в окрестности устойчивого положения равновесия система совершает незатухающие малые колебания, то линейное сопротивление превратит их в затухающие или сделает даже затухающими движениями.

1.2.3. Вынужденные колебания системы без учета сопротивления

Для возбуждения вынужденных колебаний необходимо действие на точки механической системы возмущения в этой или иной форме. Наиболее часто встречаются случаи силового и кинетического возбуждений. Рассмотрим эти случаи на примере прямолинейных колебаний груза массой по горизонтальной гладкой плоскости (рис.9, а) под действием пружины, жесткость которой .

а) б)

Рис. 9

Пусть на груз дополнительно действует зависящая от времени сила . У груза одна степень свободы. Связи (гладкая поверхность) являются идеальными. Составим для движения груза уравнение Лагранжа, приняв за обобщенную координату, отсчитываемую от положения груза, при котором пружина не деформирована. Имеем

.

Силы сопротивления отсутствуют, т.е. . Кинетическая энергия груза

.

Потенциальная энергия и обобщенная сила

; .

Для обобщенной силы получаем

,

где – возможное перемещение груза в направлении возрастания .

Вычислим производные от кинетической энергии. Имеем

; ; .

Подставляем полученные величины в уравнение Лагранжа, получаем

или .

В случае гармонической возмущающей силы

,

где , и - постоянные величины. Уравнение движения груза принимает форму

.

Предположим в этой задаче о движении груза, что сила , а следовательно, и , но вместо этого задано движение конца пружины – точки в направлении оси - в форме (рис. 9, б). Составим уравнение Лагранжа для груза относительно подвижной системы отсчета , начало которой движется вместе с точкой так, что остается все время постоянным. В этом случае по-прежнему

.

Кинетическая энергия груза

,

так как движение груза можно рассматривать как сложное, состоящее из переносного поступательного вместе с точкой и относительного по отношению к теперь уже подвижной системе координат . По теореме о сложении скоростей скорость абсолютного движения равна сумме скоростей переносного и относительного движений, т.е. . Для производных от кинетической энергии имеем:

; ; .

Подставляя полученные величины в уравнение Лагранжа, получим

; .

Роль обобщенной силы в этом уравнении выполняет величины – . Если точка совершает гармонические колебания, то

,

где , , - постоянные величины. В этом случае

и дифференциальное уравнение движения груза примет форму

,

т.е. то же, что и в первом случае, но .

Если вместо задать скорость точки , изменяющуюся по гармоническому закону

,

то уравнение движения груза примет вид

и в этом случае .

Существенное различие этих случаев в том, что при силовом возбуждении не зависит от круговой частоты . При кинематическом возбуждении заданием движения точки оно пропорционально , а при возбуждении заданием скорости точки – пропорционально . Силовое возбуждение эквивалентно возбуждению путем задания ускорения точки .

При дальнейшем рассмотрении вынужденных колебаний ограничимся случаем силового возбуждения.

Пусть обобщенная сила состоит из двух сил: потенциальной и гармонической возмущающей .

Часть обобщенной силы , зависящую от сил сопротивления, считаем равной нулю. Постоянные , и , характеризующие гармоническую возмущающую силу, соответственно являются амплитудой, круговой частотой и начальной фазой этой силы. В этом случае, как и в случае собственных линейных колебаний, из уравнения Лагранжа в предположении, что для кинетической и потенциальной энергий справедливы формулы (2) и (3), получаем дифференциальное уравнение

. (37)

Разделим обе части (37) на и введем обозначения , .

Здесь – круговая частота собственных колебаний, – относительная амплитуда возмущающей силы.

Дифференциальное уравнение вынужденных колебаний без сопротивления в окончательной форме имеет вид

. (38)

Получено неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решение, согласно теории дифференциальных уравнений, состоит из общего решения однородного уравнения и частотного решения неоднородного уравнения . Общее решение уравнения (38) есть сумма этих двух решений, т.е. .

Однородное уравнение для определения , т.е. уравнение , совпадает с дифференциальным уравнением собственных колебаний. Поэтому его решение называют собственным колебанием системы. Оно может быть выражено в двух эквивалентных формах:

. (39)

Часть движения системы, характеризуемая функцией , является частным решением уравнения (38). Эту часть движения называют вынужденным колебанием системы. Функция определяется по-разному в зависимости от соотношения частот собственных колебаний и возмущающей силы.

Возможны два случая: отсутствие резонанса и резонанс при . Рассмотрим их.

1.Случай отсутствия резонанса. В случае отсутствия резонанса и частное решение следует искать в этой же форме, что и правая часть уравнения (38):

. (40)

Постоянная подлежит определению из условий, что функция является частным решением уравнения (38) и, следовательно, подстановка в это уравнение должна обратить его в тождество. Определим необходимые производные по времени от :

; .

Подставляя и ее производные в уравнение (38) и перенося все члены в одну часть, получаем следующее тождество, справедливое в любой момент времени:

.

Так как синус переменного аргумента равен нулю не для всех значений , то полученное тождество выполняется, если постоянный коэффициент в скобках при синусе равен нулю:

.

Отсюда

.

Подставляя значение в , получаем вынужденные колебания в форме

. (41)

Таким образом, движение системы характеризуется обобщенной координатой , состоящей их двух колебаний с различными частотами – собственных с круговой частотой и вынужденных с круговой частотой :

. (42)

В амплитудной форме

. (42')

Постоянные и или и определяются из начальных условий , , .

Подставляя эти значения в выражения (42) для и при , получаем

, .

Отсюда

, .

Амплитуда собственных колебаний и начальная фаза через и выражаются формулами

; .

Следовательно, амплитуда и начальная фаза собственных колебаний при действии возмущающей силы зависит не только от начальных условий, но и от параметров этой силы, т.е. собственные колебания в этом случае могут возникнуть не только из-за начальных условий, но и благодаря действию возмущающих сил даже при нулевых начальных условиях.

Введем амплитуду вынужденных колебаний . Тогда в зависимости от соотношения между частотами вынужденные колебания можно выразить в двух формах:

при

,

при

.

Следовательно, при фаза вынужденных колебаний совпадает с фазой возмущающей силы. В этом случае сдвиг фаз между ними равен нулю, т.е. вынужденные колебания и возмущающая сила, в частности, достигают одновременно максимальных и минимальных значений.

При сдвиг фаз . Действительно, сдвиг фаз как разность фаз между возмущающей силой и вынужденными колебаниями

.

В этом случае вынужденные колебания находятся в противоположной фазе по отношению к возмущающей силе, т.е., в частности, если возмущающая сила достигает максимума, то функция достигает минимума, и наоборот.

Итак, вынужденные колебания системы без сопротивления при , возбуждаемые гармонической возмущающей силой, являются гармоническими колебаниями с постоянной амплитудой. Их частота совпадает с частотой возмущающей силы. Они совершенно не зависят от начальных условий.

2. Случай резонанса. Резонансом называется случай совпадения частот собственных колебаний и возмущающей силы, т.е. когда . При совпадении частот частное решение уравнения (38) следует искать в форме .

Постоянная определяется из условия, что есть частное решение уравнения (38), обращающее его в тождество. Аналогично рассмотренному случаю, подставив и ее производные в (38) и приравняв нулю постоянный коэффициент при [члены с взаимно уничтожаются], получаем . Тогда вынужденные колебания выразятся в форме

. (43)

Главной особенностью вынужденных колебаний при резонансе является зависимость их амплитуды от времени:

.

Амплитуда вынужденных колебаний в этом случае увеличивается пропорционально времени. Сдвиг фаз при резонансе, как это следует из (43) равен .Круговая частота вынужденных колебаний при резонансе совпадает с круговой частотой возмущающей силы.

З

Рис. 10

аметим для построения графика вынужденных колебаний при резонансе, что изменяется в пределах от до . Следовательно, согласно (43), графиком вынужденных колебаний является синусоида, заключенная между двумя прямыми и , проходящими через точки и (рис. 10).

Рассмотренный случай колебаний при резонансе без сопротивления практически не встречается, так как при движении системы всегда есть силы сопротивления движения. Установленный теоретически рост амплитуды с течением времени по линейному закону в действительности тоже не наблюдается, хотя амплитуды при резонансе достигают довольно больших значений по сравнению со случаем отсутствия резонанса. Эта особенность вынужденных колебаний при резонансе приводит к тому, что случайно возникший резонанс в машинах, установках и сооружениях (мосты, роторы турбин, полы зданий и т. д.) может привести к их разрушению.

Построим для вынужденных колебаний графики амплитуды и сдвига фаз в зависимости от круговой частоты возмущающейся силы. Имеем

при или ,

где введено обозначение (рис. 11).

При величина , но при эту формулу для амплитуды вынужденных колебаний применять нельзя.. Справедлива другая формула: .

Г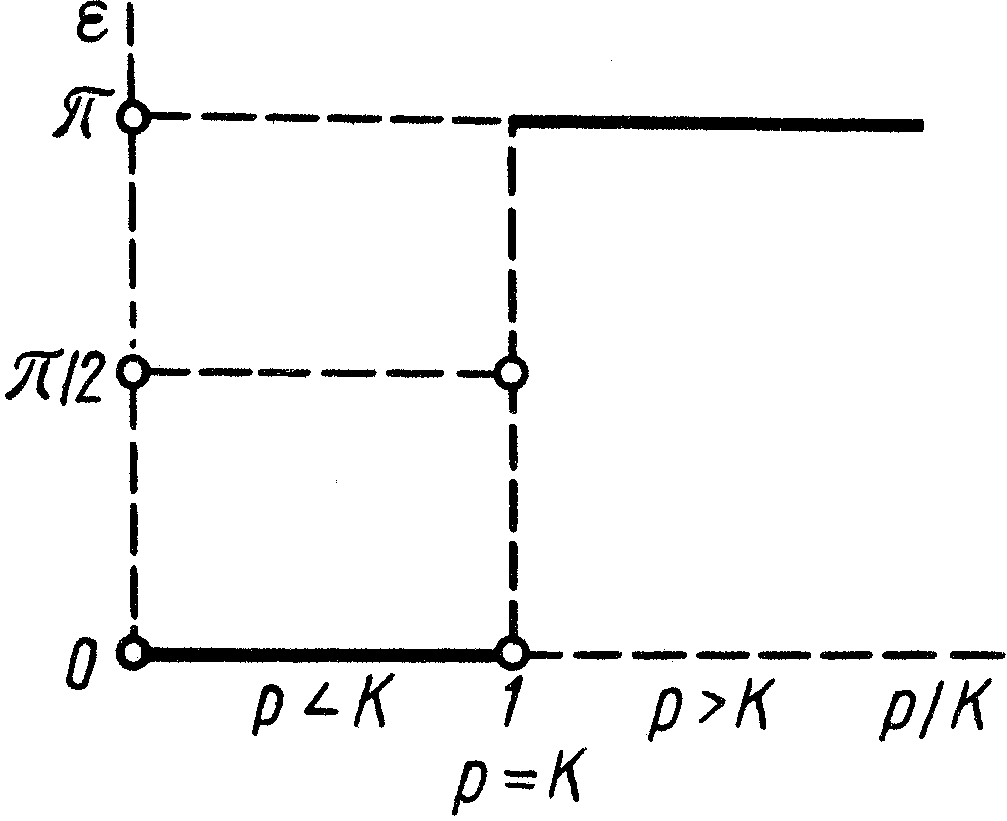 рафик зависимости от (рис. 12) состоит из двух отрезков горизонтальных прямых и одной точки, так как при ; при .

Рис. 11 Рис.12

1.2.4. Влияние линейного сопротивления

на вынужденные колебания

Дифференциальное уравнение

вынужденных колебаний и его интегрирование

Для выяснения влияния линейного сопротивления на вынужденные колебания рассмотрим наиболее общий случай, когда обобщенная сила состоит их трех сил: потенциальной , линейного сопротивления и гармонической возмущающей .

Подставляя это значение обобщенной силы в уравнение Лагранжа (1), получаем

.

Разделим обе части уравнения на и введем обозначения , , . Здесь – круговая частота собственных колебаний; – коэффициент затухания и – относительная амплитуда возмущающей силы.

Дифференциальное уравнение в окончательной форме

. (44)

Получено линейное дифференциальное уравнение с постоянными коэффициентами вынужденных колебаний с учетом линейного сопротивления.

Так как оно является неоднородным уравнением, то его решение состоит из двух частей: – общего решения однородного уравнения, – частного решения неоднородного уравнения. Общее решение однородного уравнения удовлетворяет уравнению собственных колебаний при линейном сопротивлении, поэтому его называют собственным движением или даже собственными колебаниями, хотя это движение может и не быть колебательным.

Частое решение неоднородного уравнения называют вынужденным колебанием. Общее движение системы характеризуется обобщенной координатой , которая равна сумме и , т.е. . Величину называют общим вынужденным движением (или вынужденным колебанием).

Общее решение однородного дифференциального уравнения в зависимости от соотношения между величинами и выражается в одной их трех форм:

, ;

, ;

, .

Известно, что в любом из трех случаев из-за наличия множителя стремится к нулю с возрастанием времени, т.е. затухает. При малых значениях коэффициента затухания затухающее движение носит колебательный характер, а при больших затухание так велико, что движение не является колебательным. Следовательно, при наличии линейного сопротивления по истечении достаточного времени общее вынужденное движение несущественно отличается от вынужденных колебаний и можно считать, что .

Частное решение уравнения (44) следует искать в форме .

Постоянные и определяются из следующего условия: если подставить в уравнение (44), то оно превратится в тождество. Вычислим для этого производные от :

; .

Преобразуем правую часть уравнения (44) так, чтобы в нее входили косинус и синус такого же аргумента, что и у функции . Для этого следует к фазе правой части прибавить и вычесть величину и раскрыть синус суммы:

.

Учитывая это, подставим значение и его производных в уравнение (44) и соберем члены при и . Получим тождество

.

Так как синус и косинус переменного аргумента не равны нулю одновременно, то тождество может выполняться только тогда, когда каждая из постоянных в квадратных скобках равна нулю, т.е.

; .

Из этих уравнений определяем амплитуду вынужденных колебаний и сдвиг фаз :

, ,

, .

Из формулы для следует, что является положительной величиной. Следовательно, значения заключены между и . Поэтому для определения достаточно использовать формулу только одной тригонометрической функции, например для .

Окончательная форма выражения вынужденных колебаний

, (45)

где

, , . (46)