
- •В. Н. Веретенников
- •ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- •Учебное пособие
- •ПРЕДИСЛОВИЕ
- •ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- •1. Физические задачи, приводящие к дифференциальным уравнениям
- •Биография
- •Увековечение памяти
- •Научные достижения
- •Математика
- •Точка Торричелли
- •Механика
- •Атмосферное давление и первый барометр
- •Гидравлика
- •Изобретения
- •2. Дифференциальные уравнения первого порядка
- •2.1. Основные понятия
- •2.2. Эквивалентные дифференциальные уравнения. Задача Коши
- •Общее и частное решения уравнения.
- •Итак, чтобы найти особые решения уравнения (2.2), надо
- •Геометрический смысл уравнения.
- •2.4. Уравнения с разделяющимися переменными
- •2.5. Однородные дифференциальные уравнения 1-го порядка
- •Биография
- •Научная деятельность
- •Биография
- •Метод вариации постоянной (Лагранжа).
- •Уравнения Бернулли.
- •3. Дифференциальные уравнения второго порядка.
- •3.1. Задача Коши
- •3.2. Уравнения 2 - го порядка, допускающие понижение порядка
- •3.2.2. Уравнение вида
- •3.2.3. Уравнение вида
- •4. Дифференциальные уравнения высших порядков
- •Уравнения высших порядков, допускающие понижение порядка
- •5. Однородные линейные дифференциальные уравнения n-го порядка
- •5.1. Свойства решений однородного линейного уравнения
- •5.2. Линейно зависимые и линейно независимые системы функций
- •Биография
- •Философские воззрения
- •Научные достижения

При выполнении всех этихусловий найденная кривая представляет собой особое решение уравнения (2.2).
Геометрический смысл уравнения.
Геометрическая интерпретация дифференциального уравнения (2.2) состоит в том, что оно в каждой точке M (x; y) , принадлежащей области G, в которой выполняются все условия
теоремы Коши 2.1, задает направление y′ = tgα = k касательной к единственной линии уравнения (2.2), проходящей через точку M (x; y) , т. е. поле направлений в области G.
ВобластиG дляуравнения(2.2) можновыделитьоднопараметрическоесемействолиний f (x; y) = k = const , каждая из которых называется изоклиной. Как следует из определения,
вдоль каждой изоклины поле направлений постоянно, т. е. y′ = k = const .
Нахождениеизоклининаправленийвдольнихпозволяетупорядочитьполенаправлений и приближенно построить интегральные линии данного дифференциального уравнения, т. е. графически проинтегрировать это уравнение.
2.4. Уравнения с разделяющимися переменными
Рассмотрим методы нахождения решений дифференциальных уравнений 1-го порядка. Отметим, что общего метода нахождения решений не существует. Обычно рассматривают типы уравнений, и для каждого из них находят свой способ нахождения решения.
Уравнение вида
y′ = f1 (x) f2 (y) , |
(4.1) |
где f1 (x) и f2 (x) − непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными.
Для отыскания решения уравнения (2.5) нужно, как говорят, разделить в нем переменные. Для этого
заменим в (2.5) y′ на dydx , умножим на дифференциал dx ,
разделим обе части уравнения на f2 (y) (f2 (y) ≠ 0). Тогда уравнение (2.5) принимает вид
dy |
= f1 (x)dx . |
(4.2) |
|
f2 (y) |
|||
|
|
В этом уравнении переменная x входит только в правую часть уравнения, а переменная y − только в левую часть. Следовательно, переменные разделены.
Покажем, как найти решение этого уравнения. Пусть F1(x) и F2 (y) − первообразные функции f1(x) и f21( y) соответственно. Равенство (4.2) равносильно тому, что дифференциалы этих функций должны совпадать dF2 (y) = dF1 (x) .
Отсюда следует, что F2 (y) = F1 (x) + C , где C − произвольная постоянная величина.
Разрешая последнее уравнение относительноy, получим функцию (может быть, и не одну) y =ϕ(x) , которая обращает уравнение (4.2) в тождество и значит, является его решением.
Пример 4.1. Найти общее решение дифференциального уравнения (1+e2x )y2 y′ = ex . ▲ Заменим y′ на dydx , умножим уравнение на dx и разделим переменные
(1+e2x )y2 dy |
= ex |
|
dx, (1+e2x )y2dy = exdx |
: (1+e2x ), y2dy = |
exdx |
. |
|
||||||
|
|
|||||
dx |
|
|
|
|
1+e2x |
|
|
|
|
|
|||
Проинтегрируем последнее уравнение с разделенными переменными:
12
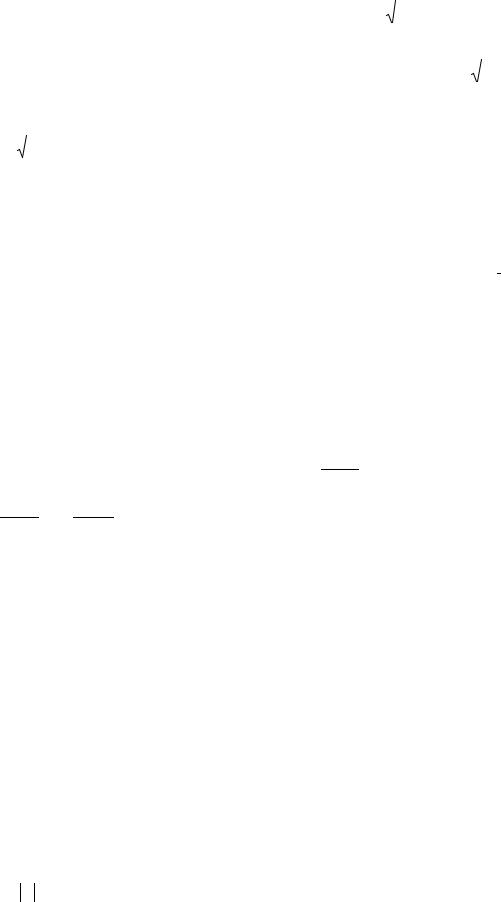
∫y |
2 |
dy = ∫ |
exdx |
y3 |
= ∫ |
|
|
d(ex ) |
y3 |
|
|
|
|
x |
|
C |
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
x |
|
||||||||||||||||||||||||||
|
|
, |
|
|
|
|
|
|
|
|
|
|
, |
|
|
= arctg e |
|
+ 3 , y = 3 C +3arctg e |
|
|
|
|||||||||||||
|
1+e2x |
3 |
1+(ex )2 |
3 |
|
|
|
|
||||||||||||||||||||||||||
Получили общее решение исходного уравнения. ▼ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Пример4.2.Найтичастноерешениедифференциальногоуравнения y′ = 3 3 |
y2 |
, удовле- |
||||||||||||||||||||||||||||||||
творяющее начальному условию y(1) =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
▲ Полагая y ≠ 0 , разделяя переменные и интегрируя, получаем |
|
|
|
|
|
|
||||||||||||||||||||||||||||
dy = 3 3 y |
2 |
dx, dy = 3y 3 dx : y 3 , dy2 = 3dx, |
|
y−3 dy = |
|
3dx, |
y3 = x +C, y = (x +C)3 . |
|||||||||||||||||||||||||||
dx |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
y |
|
|
|
|
|
∫ |
2 |
|
|
∫ |
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Получили общее решение исходного уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Подставляя начальные данные x0 =1, y0 |
=1 в формулу для общего решения y = (x +C)3 |
|||||||||||||||||||||||||||||||||
, находим значение C: 1 = (1+C)3 , C = 0 . y = x3 − искомое частное решение. |
|
|
|
|
||||||||||||||||||||||||||||||
Очевидно, |
y = 0 − также решение уравнения, это решение является особым: в каждой |
|||||||||||||||||||||||||||||||||
2
точке оси Ox нарушаются условия теоремы 2.1 (производная функции f (x; y) = 3y 3 по y обращается в бесконечность). Через каждую точку M0 (x0 ; 0) оси Ox проходят два решения y = (x − x0 )3 и y = 0 ; последнее решение нельзя получить из общего решения y = (x +C)3 , ни при каком численном значении C, включая C = ±∞ (а только приC = C(x) = −x ). ▼
Пусть дифференциальное уравнение задано в дифференциальной форме (2.3). Рассмотрим частный случай, а именно, когда функции P(x; y) и Q(x; y) представляют собой произ-
ведения функции только от x на функции только от y , т. е.
P(x; y) = p1(x) p2 ( y), Q(x; y) = q1(x) q2 (y) .
В этом случае уравнение (2.3) принимает вид p1(x) p2 (y)dx + q1(x) q2 (y)dy = 0. Разделив почленно это уравнение на q1 (x) p2 (y) , полагая что q1 (x) p2 ( y) ≠ 0 , получим
уравнение p1 (x) dx + q2 (y) dy = 0 . q1 (x) p2 (y)
Это уравнение называется уравнением с разделенными переменными: при dx находится функция, зависящая только от x , при dy − только от y .
Взяв неопределенный интеграл от обеих частей уравнения, получим
∫ |
p1 |
(x) |
dx + ∫ |
q2 (y) |
dy = C . |
|
q |
(x) |
p (y) |
||||
1 |
|
|
2 |
|
||
Это равенство выражает общий интеграл уравнения (2.3). В этом случае говорят, что ре- |
||||||
шение найдено «в квадратурах». |
|
|
|
|
|
|
Заметим, что деление на q1 (x) p2 (y) |
может привести к потере решений, обращающих в |
|||||
нуль произведение q1 (x) p2 ( y) . |
|
|
|
|
|
|
Пример 4.3. Найти общее решение дифференциального уравнения
(xy + y)dx +(xy + x)dy = 0 .
▲ Раскладывая функции при dx и dy на множители, полагая, что x ≠ 0, y ≠ 0 и разделив обе части данного уравнения на xy , получим уравнение с разделенными переменными:
y(x +1)dx + x(y +1)dy = 0 |
|
: xy, |
x +1 |
dx + |
y +1 |
dy = 0 . |
|
|
|||||||
|
|
|
|||||
|
|
|
|
x |
|
y |
|
|
|
|
|
||||
Интегрируя его, последовательно находим (произвольную постоянную можно представить в виде ln C ):
13

|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x+y |
|
|
|
x+y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∫ |
1+ |
|
dx + |
∫ |
|
|
|
x |
|
+ y +ln |
|
y |
|
= ln |
|
C |
|
, ln |
|
xy |
|
+ln e |
|
= ln |
C |
, xye |
= C . |
|
|
1+ |
|
dy = 0, x +ln |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Последнее равенство является общим интегралом данного уравнения. При его нахождении были приняты ограничения x ≠ 0, y ≠ 0 . Однако функции x = 0 и y = 0 также являются
решениями исходного уравнения, что легко проверяется; с другой стороны, они получаются из общего интеграла приC = 0 .
Следовательно, x = 0, y = 0 − частные решения данного уравнения. ▼
2.5. Однородные дифференциальные уравнения 1-го порядка
Определение. Функция F(x; y) называется однородной функцией измерения k относи-
тельно аргументов x и y, если равенство
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(λx; λy) = λk F(x; y) |
|
|
|
|
(5.1) |
|
|||||||||||||||||||||
|
справедливо для любого λ R , при котором функция F(λx; λy) |
определена, k = const . |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Например, функция F1 (x; y) = x + 2y является однородной первого измерения (k =1) , |
||||||||||||||||||||||||||||||||||||||||||
так как |
|
|
|
|
|
|
|
F (λx; λy) = λx + 2λy = λ(x + 2y) = λ1F (x; y) . |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
Функция F (x; y) = x2 sin |
x |
является однородной второго измерения (k = 2) , поскольку |
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (λx; λy) = (λx)2 sin |
λ x |
= λ2 x2 sin |
x |
= λ2 F (x; |
y) . |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
λ y |
y |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
Функция |
F (x; y) = |
x + y |
является однородной нулевого измерения (k = 0) , поскольку |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λx +λy |
|
|
λ(x + y) |
|
|
x + y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
F |
|
(λx; |
λy) = |
= |
|
= |
= λ0 F (x; y) . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
λx |
λx |
x |
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Функция F (x; y) = 3x4 |
− x2 y2 +5y4 является однородной четвертого измерения (k = 4) , т. к. |
||||||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (λx; λy) = 3 (λx)4 |
−(λx)2 (λy)2 +5 (λy)4 = λ4 (3x4 − x2 y2 +5y4 ) = λ4 F (x; y) . |
|||||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||||
Функция |
F (x; y) = 3 |
x2 |
|
−2 3 |
|
|
|
+ 4 3 y2 является однородной измерения k = |
2 |
, поскольку |
|||||||||||||||||||||||||||||||||
|
|
xy |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
F5 (λx; λy) = 3 (λx)2 −2 |
3 (λx)(λy) + 43 (λy)2 = 3 λ2 (3 x2 − 23 xy |
+ 43 y2 )= λ |
3 |
F5 (x; y) . |
||||||||||||||||||||||||||||||||||||||
Определение. Дифференциальное уравнение в нормальной форме (2.2) называется однороднымотносительно переменных x и y, если f (x; y) − однородная функция нулевого
измерения относительно своих аргументов, т. е.
|
|
|
|
f (λx; λy) = λ0 f (x; y) = f (x; y) |
|
|
|
(5.2) |
|
||||||||||||
|
Так как однородное дифференциальное уравнение в нормальной форме (2.2) всегда |
||||||||||||||||||||
можно записать в виде y′ = f (x; y) = f (λx; λy) , то, положив λ = |
1 |
, получим |
|
|
|
||||||||||||||||
x |
|
|
|
||||||||||||||||||
|
|
|
|
|
y′ = f (1; |
y |
)=ϕ( |
y |
). |
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
x |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
′ |
′ |
|
|
|
|
Следовательно, уравнение (2.2) с помощью замены y = tx (t = x ), y |
|
сводится к |
||||||||||||||||||
|
|
= t x +t |
|
||||||||||||||||||
уравнению с разделяющимися переменными относительно x и новой функции t(x) : |
|
|
|
||||||||||||||||||
|
′ |
|
dt |
dx, xdt = (f (1; t) −t)dx |
|
: x(f (1; t) −t), |
|
|
dt |
|
dx |
||||||||||
|
t x +t = f (1; t), |
x |
|
= f (1; t) −t |
|
|
= x . |
||||||||||||||
|
dx |
|
(f (1; t) −t) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
14
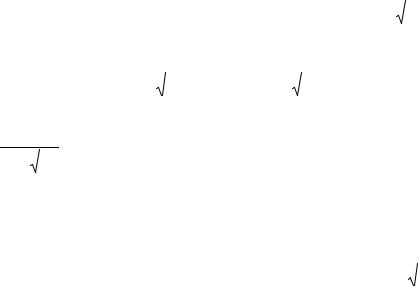
Дифференциальноеуравнениевдифференциальнойформе(2.3)будетоднороднымвтом и только в том случае, когда P(x; y), Q(x; y) − однородные функции одного и того же измере-
ния k, т. е. P(λx; λy) = λk P(x; y), Q(λx; λy) = λk Q(x; y) . |
|
|
|
|
|
|
|||
Действительно, переписав его в нормальной форме: |
y′ = − |
P(x; y) |
≡ |
f (x; y) , легко заклю- |
|||||
Q(x; y) |
|
||||||||
чаем, что f (x; y) − однородная функция нулевого измерения, поскольку |
|
||||||||
f (λx; λy) = − |
P(λx; λy) |
= − |
λk P(x; y) |
= f (x; y) . |
|
|
|||
Q(λx; λy) |
λk Q(x; y) |
|
|
||||||
|
|
|
|
|
|
|
|||
Пример 5.1. Проинтегрировать дифференциальное уравнение 2x2 y′ = x2 + y2 и найти |
|||||||||
его частное решение, удовлетворяющее начальному условию y(1) = 0 . |
|
|
|||||||
▲ Так как функции 2x2 |
|
и x2 + y2 − однородные второго измерения, то данное уравнение – |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
однородное. Сделаем замену y = tx, |
y |
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
= t x +t . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2x |
2 |
′ |
|
|
|
|
|
2 |
|
+(tx) |
2 |
, 2x |
2 |
′ |
2 |
(1+t |
2 |
) . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(t x +t) = x |
|
|
|
|
|
(t x +t) = x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Предполагая, что x ≠ 0 , сокращаем обе части уравнения на x2 . Далее имеем |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2x |
dt |
|
+2t =1+t2 |
|
dx, 2xdt = (1+t2 −2t)dx |
|
|
: 2x(1−2t +t2 ) . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
dx |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разделив переменные, последовательно находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
dt |
|
dx |
|
|
|
|
d(t −1) |
|
|
1 |
|
dx |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, 1 = (1−t)ln(C |
|
|
|
). |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
= 2x , ∫ (t −1)2 |
= |
|
2 |
∫ |
|
x , − |
|
|
|
= |
2 ln |
|
x |
|
+ln |
|
C |
|
|
x |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
(t −1)2 |
|
|
t −1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
В последнее равенство вместоt |
подставим значение |
y |
. Получим общий интеграл |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 = 1− |
y |
ln(C |
|
|
|
|
|
|
), x = (x − y)ln(C |
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Разрешив его относительно y, найдем общее решение исходного дифференциального |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнения: y = x − |
ln(C |
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Используя начальное условие y(1) = 0 , определим значение C: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 =1− |
|
1 |
, lnC =1, C = e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||
Следовательно, частное решение исходного уравнения имеет вид |
y = x − |
. ▼ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1+ln |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
15
