
- •Preface
- •Contents
- •1 Introduction
- •1.1 Physics
- •1.2 Mechanics
- •1.3 Integrating Numerical Methods
- •1.4 Problems and Exercises
- •1.5 How to Learn Physics
- •1.5.1 Advice for How to Succeed
- •1.6 How to Use This Book
- •2 Getting Started with Programming
- •2.1 A Python Calculator
- •2.2 Scripts and Functions
- •2.3 Plotting Data-Sets
- •2.4 Plotting a Function
- •2.5 Random Numbers
- •2.6 Conditions
- •2.7 Reading Real Data
- •2.7.1 Example: Plot of Function and Derivative
- •3 Units and Measurement
- •3.1 Standardized Units
- •3.2 Changing Units
- •3.4 Numerical Representation
- •4 Motion in One Dimension
- •4.1 Description of Motion
- •4.1.1 Example: Motion of a Falling Tennis Ball
- •4.2 Calculation of Motion
- •4.2.1 Example: Modeling the Motion of a Falling Tennis Ball
- •5 Forces in One Dimension
- •5.1 What Is a Force?
- •5.2 Identifying Forces
- •5.3.1 Example: Acceleration and Forces on a Lunar Lander
- •5.4 Force Models
- •5.5 Force Model: Gravitational Force
- •5.6 Force Model: Viscous Force
- •5.6.1 Example: Falling Raindrops
- •5.7 Force Model: Spring Force
- •5.7.1 Example: Motion of a Hanging Block
- •5.9.1 Example: Weight in an Elevator
- •6 Motion in Two and Three Dimensions
- •6.1 Vectors
- •6.2 Description of Motion
- •6.2.1 Example: Mars Express
- •6.3 Calculation of Motion
- •6.3.1 Example: Feather in the Wind
- •6.4 Frames of Reference
- •6.4.1 Example: Motion of a Boat on a Flowing River
- •7 Forces in Two and Three Dimensions
- •7.1 Identifying Forces
- •7.3.1 Example: Motion of a Ball with Gravity
- •7.4.1 Example: Path Through a Tornado
- •7.5.1 Example: Motion of a Bouncing Ball with Air Resistance
- •7.6.1 Example: Comet Trajectory
- •8 Constrained Motion
- •8.1 Linear Motion
- •8.2 Curved Motion
- •8.2.1 Example: Acceleration of a Matchbox Car
- •8.2.2 Example: Acceleration of a Rotating Rod
- •8.2.3 Example: Normal Acceleration in Circular Motion
- •9 Forces and Constrained Motion
- •9.1 Linear Constraints
- •9.1.1 Example: A Bead in the Wind
- •9.2.1 Example: Static Friction Forces
- •9.2.2 Example: Dynamic Friction of a Block Sliding up a Hill
- •9.2.3 Example: Oscillations During an Earthquake
- •9.3 Circular Motion
- •9.3.1 Example: A Car Driving Through a Curve
- •9.3.2 Example: Pendulum with Air Resistance
- •10 Work
- •10.1 Integration Methods
- •10.2 Work-Energy Theorem
- •10.3 Work Done by One-Dimensional Force Models
- •10.3.1 Example: Jumping from the Roof
- •10.3.2 Example: Stopping in a Cushion
- •10.4.1 Example: Work of Gravity
- •10.4.2 Example: Roller-Coaster Motion
- •10.4.3 Example: Work on a Block Sliding Down a Plane
- •10.5 Power
- •10.5.1 Example: Power Exerted When Climbing the Stairs
- •10.5.2 Example: Power of Small Bacterium
- •11 Energy
- •11.1 Motivating Examples
- •11.2 Potential Energy in One Dimension
- •11.2.1 Example: Falling Faster
- •11.2.2 Example: Roller-Coaster Motion
- •11.2.3 Example: Pendulum
- •11.2.4 Example: Spring Cannon
- •11.3 Energy Diagrams
- •11.3.1 Example: Energy Diagram for the Vertical Bow-Shot
- •11.3.2 Example: Atomic Motion Along a Surface
- •11.4 The Energy Principle
- •11.4.1 Example: Lift and Release
- •11.4.2 Example: Sliding Block
- •11.5 Potential Energy in Three Dimensions
- •11.5.1 Example: Constant Gravity in Three Dimensions
- •11.5.2 Example: Gravity in Three Dimensions
- •11.5.3 Example: Non-conservative Force Field
- •11.6 Energy Conservation as a Test of Numerical Solutions
- •12 Momentum, Impulse, and Collisions
- •12.2 Translational Momentum
- •12.3 Impulse and Change in Momentum
- •12.3.1 Example: Ball Colliding with Wall
- •12.3.2 Example: Hitting a Tennis Ball
- •12.4 Isolated Systems and Conservation of Momentum
- •12.5 Collisions
- •12.5.1 Example: Ballistic Pendulum
- •12.5.2 Example: Super-Ball
- •12.6 Modeling and Visualization of Collisions
- •12.7 Rocket Equation
- •12.7.1 Example: Adding Mass to a Railway Car
- •12.7.2 Example: Rocket with Diminishing Mass
- •13 Multiparticle Systems
- •13.1 Motion of a Multiparticle System
- •13.2 The Center of Mass
- •13.2.1 Example: Points on a Line
- •13.2.2 Example: Center of Mass of Object with Hole
- •13.2.3 Example: Center of Mass by Integration
- •13.2.4 Example: Center of Mass from Image Analysis
- •13.3.1 Example: Ballistic Motion with an Explosion
- •13.4 Motion in the Center of Mass System
- •13.5 Energy Partitioning
- •13.5.1 Example: Bouncing Dumbbell
- •13.6 Energy Principle for Multi-particle Systems
- •14 Rotational Motion
- •14.2 Angular Velocity
- •14.3 Angular Acceleration
- •14.3.1 Example: Oscillating Antenna
- •14.4 Comparing Linear and Rotational Motion
- •14.5 Solving for the Rotational Motion
- •14.5.1 Example: Revolutions of an Accelerating Disc
- •14.5.2 Example: Angular Velocities of Two Objects in Contact
- •14.6 Rotational Motion in Three Dimensions
- •14.6.1 Example: Velocity and Acceleration of a Conical Pendulum
- •15 Rotation of Rigid Bodies
- •15.1 Rigid Bodies
- •15.2 Kinetic Energy of a Rotating Rigid Body
- •15.3 Calculating the Moment of Inertia
- •15.3.1 Example: Moment of Inertia of Two-Particle System
- •15.3.2 Example: Moment of Inertia of a Plate
- •15.4 Conservation of Energy for Rigid Bodies
- •15.4.1 Example: Rotating Rod
- •15.5 Relating Rotational and Translational Motion
- •15.5.1 Example: Weight and Spinning Wheel
- •15.5.2 Example: Rolling Down a Hill
- •16 Dynamics of Rigid Bodies
- •16.2.1 Example: Torque and Vector Decomposition
- •16.2.2 Example: Pulling at a Wheel
- •16.2.3 Example: Blowing at a Pendulum
- •16.3 Rotational Motion Around a Moving Center of Mass
- •16.3.1 Example: Kicking a Ball
- •16.3.2 Example: Rolling down an Inclined Plane
- •16.3.3 Example: Bouncing Rod
- •16.4 Collisions and Conservation Laws
- •16.4.1 Example: Block on a Frictionless Table
- •16.4.2 Example: Changing Your Angular Velocity
- •16.4.3 Example: Conservation of Rotational Momentum
- •16.4.4 Example: Ballistic Pendulum
- •16.4.5 Example: Rotating Rod
- •16.5 General Rotational Motion
- •Index
384 |
12 Momentum, Impulse, and Collisions |
and conservation of kinetic energy is now:
v2A,0 = v2A,1 + v2B,1 . |
|
|
|
(12.115) |
||
We insert v A,0 into (12.115): |
|
|
|
|
|
|
|
v2A,0 = v2A,1 + v2B,1 |
|
||||
2 |
2 |
2 |
1 |
2 |
1 |
|
v A,1 |
+ vB,1 |
2 = v2A, |
|
+ v2B, |
|
(12.116) |
vA,1 + 2v A,1 · vB,1 + vB,1 = vA,1 + vB,1
2v A,1 · vB,1 = 0 ,
We have found that v A,1 · vB,1 = 0, which means that the two velocities are orthogonal! Notice that we still do not have enough equations to determine the vectors: We have 3 equations, but 4 unknown components in the velocity vectors after the collision. In order to determine the velocities after the collision we need more information about the collision. We need to know something about the force acting between the particles throughout the collision.
12.6 Modeling and Visualization of Collisions
We can gain better insights into the concepts introduced in this chapter by studying collisions in detail. If we know the details of the interactions between two objecst, that is, if the have models for the interaction forces, we can find their motion from Newton’s second law.Let us use this to get a better understanding of elastic, inelastic and perfectly inelastic collisions.
We model two objects, A and B, with masses m A and m B . The force from B on A is:
FB on A = F(r A , r B , v A , vB ) , |
(12.117) |
and from Newton’s third law, we know that
FA on B = −F . |
(12.118) |
For example, for two solid spheres of radius R, a reasonable force model is:
F = |
|
2 |
0 |
r |
, |
r ≥ 2R |
, |
(12.119) |
|
k | r − |
|
R| |
r − η ( |
v) , |
r < 2R |
|
|
12.6 Modeling and Visualization of Collisions |
385 |
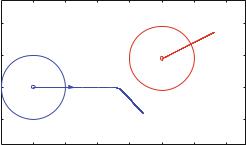
Fig. 12.17 Illustration of object trajectories and initial conditions
y [m]
0.04
0.02
0
−0.02
−0.02 |
0 |
0.02 |
0.04 |
0.06 |
0.08 |
0.1 |
0.12 |
|
|
|
|
x [m] |
|
|
|
where r = r B − r A , r = | r| and v = vB − v A . We find the equation of motion from Newton’s second law:
m A a A = F a A = |
F |
(12.120) |
|
|
. |
||
|
|||
|
m A |
|
|
We find the motion of both objects from Euler-Cromer’s method, as implemented in the following program. First, we define the masses, the radius, and the initial positions and velocities of the objects:
from pylab import * R = 0.02 # m
mA = 0.1 # kg mB = 0.1 # kg
rA0 = array([0.0,0.0]) # m vA0 = array([1.0,0.0]) # m/s rB0 = array([0.08,0.018]) # m vB0 = array([0.0,0.0]) # m/s time = 0.10 # s
This set of initial conditions are illustrated in Fig. 12.17. These conditions will result in an non-central collision. Then, we define the parameters used by the force model, such as the force constant k and the viscous term η. We choose an unrealistically small value for k in order to make the collision extend over some time so that we can observe the interactions during the collision. The time step is chosen small enough, so that we are sure to have good resolution for the motion during the collision:
# Force model eta = 1.0
k = 20000.0 # Nm dt = 0.0001 # s
We initialize by generating arrays for all the variables:
# Initialization
n = int(round(time/dt)) t = zeros(n,float)
rA = zeros((n,2),float) vA = zeros((n,2),float) rB = zeros((n,2),float) vB = zeros((n,2),float)
386 |
12 Momentum, Impulse, and Collisions |
F = zeros((n,2),float) |
|
rA[0] = rA0 |
|
vA[0] = vA0 |
|
rB[0] = rB0 |
|
vB[0] = vB0 |
|
D = 2*R # Diameter |
|
Where we have introduce the diameter, D = 2R, to simplify the expressions. The integration loop follows the mathematical formulation of the force law in (12.119) as closely as possible:
# Integration loop for i in range(n-1):
Deltar = rB[i]-rA[i]
Deltarnorm = sqrt(dot(Deltar,Deltar)) Deltav = vB[i]-vA[i]
if (Deltarnorm>=D): Fnet = array([0,0])
else:
Fnet = -k*abs(Deltarnorm-D)**1.5*Deltar/Deltarnorm + eta*Deltav; F[i] = Fnet
aA = Fnet/mA aB = -Fnet/mB
vA[i+1] = vA[i] + aA*dt rA[i+1] = rA[i] + vA[i+1]*dt vB[i+1] = vB[i] + aB*dt rB[i+1] = rB[i] + vB[i+1]*dt t[i+1] = t[i] + dt
Finally, we plot the resulting trajectories and the momentum in the x and y direction as functions of time:
# Plot trajectories and momentum figure(1)
plot(rA[:,0],rA[:,1],’-b’,rB[:,0],rB[:,1],’-r’) xlabel(’x [m]’)
ylabel(’y [m]’) axis(’equal’) figure(2)
pA = vA.copy()*mA pB = vB.copy()*mB subplot(2,1,1)
plot(t,pA[:,0],’-b’,t,pB[:,0],’-r’) xlabel(’t [s]’)
ylabel(’p_x [kgm/s]’) subplot(2,1,2)
plot(t,pA[:,1],’-b’,t,pB[:,1],’-r’); xlabel(’t [s]’)
ylabel(’p_y [kgm/s]’);
While these plots provide useful information about the collision, and we can use them to gain intuition about collisions, we may also learn from seeing the dynamics of the collision—how the objects move. This can be done by generating a simple animation using the plot command:
# Animate using plot figure(3)
for i in range(0,n,50): plot(rA[:,0],rA[:,1],’-b’,rB[:,0],rB[:,1],’-r’,
[rA[i,0]],[rA[i,1]],’ob’,[rB[i,0]],[rB[i,1]],’or’) xlabel(’x [m]’)
ylabel(’y [m]’) axis(’equal’)
