1.4. Уравнения движения жидкости в напряжениях.

П олучим общие уравнения движения жидкости, устанавливающие связь между внешними и внутренними силами, действующими на нее.

Выделим в движущейся жидкости произвольный жидкий объем V, ограниченный поверх-ностью S (рис.5), а внутри этого объема – элемен-тарную частицу с массой dV и поверхностью dS. К этой частице приложены массовые силы с напря-жением и поверхностные силы с напряжением . Запишем уравнение движения этой частицы, исходя из второго закона Ньютона, обозначая ускорение центра тяжести частицы ,

. (1.14)

Просуммируем левую и правую части этого уравнения. Суммирование первых двух членов сводится к интегрированию по объему, а третьего члена – по площадкам, которыми элементарные частицы соприкасаются друг с другом. Согласно третьему закону Ньютона, поверхностные силы по всем внутренним площадкам взаимно уничтожаются, останутся только поверхностные силы по площади S, ограничивающей объем V,

. (1.15)

Преобразуем третий член (1.15), используя зависимость (1.9),

. (1.16)

Применим к правой части этого равенства преобразование Гаусса-Остроградского, устанавливающее связь между объемным и поверхностным интегралами,

(1.17)

Подставляя левую часть (1.17) в уравнение (1.15), получим

(1.18)

Все члены в уравнении (1.18) интегрируются по объему. Уравнения (1.15) и (1.18) являются уравнениями движения жидкого объема в интегральной форме. При этом левая часть представляет собой главный вектор сил инерции, первое слагаемое правой части – главный вектор массовых сил, второе – главный вектор поверхностных сил.

Получим дифференциальную форму уравнения движения, более удобную для изучения движения жидкости. Объединим все члены уравнения (1.18) под знаком интеграла, перенося силу инерции в правую часть,

. (1.19)

Ввиду произвольности объема этот интеграл обращается в ноль только тогда, когда нулю равна подынтегральная функция

. (1.20)

В итоге получим дифференциальное уравнение движения жидкости в напряжениях

, (1.21)

которое связывает ускорения с напряжениями массовых и поверхностных сил в данной точке потока и справедливо как для вязкой, так и для невязкой жидкости.

Проектирую векторное уравнение (1.21) на оси координат, будем иметь систему трех скалярных уравнений

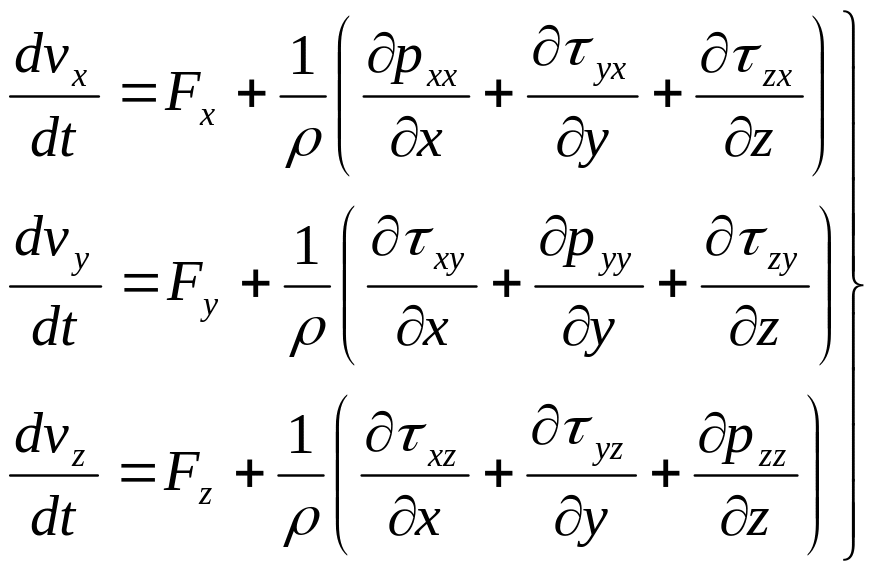(1.22)

Эта система основных уравнений движения жидкости, служащая для разработки гидродинамики вязкой и невязкой жидкости.

Уравнения движения жидкости в напряжениях (1.22) не могут быть проинтегрированы, т.е. решены в общем случае, так как система уравнений незамкнута – три уравнения при двенадцати неизвестных. Далее будет показано, что в определенных случаях движения жидкости система (1.22) упрощается и может быть получено решение, позволяющее определить силовое взаимодействие между жидкостью и твердым телом или между потоком жидкости и твердыми стенками.

Глава II

Гидростатика

2.1. Уравнения равновесия и их интегрирование. Основное уравнение гидростатики.

Гидростатика – раздел гидромеханики, изучающий равновесие жидкости. Различают абсолютное равновесие жидкости, когда из массовых сил действует лишь сила тяжести, и относительное равновесие, когда на жидкость, кроме сил тяжести, действуют инерционные силы. В этом случае объем жидкости может двигаться, не деформируясь, как твердое тело, когда движение частиц друг относительно друга отсутствует.

В этом разделе будет рассмотрена гидростатика несжимаемой жидкости. В силу этого полученные выводы будут полностью справедливы только для практически несжимаемых капельных жидкостей. Для воздуха (газа) полученные зависимости можно применять, если разность высот в рассматриваемом объеме жидкости незначительны. В противном случае необходимо учитывать зависимость плотности от высоты места и температуры.

Связь между массовыми и поверхностными силами в жидкости, находящейся в равновесии, устанавливается уравнениями равновесия, для получения которых необходимо в формуле (1.21) ускорение жидкости приравнять нулю. Кроме этого необходимо учесть, что в покоящейся жидкости касательные напряжения равны нулю, а нормальные напряжения по условию (1.13) характеризуются давлениями.

Учитывая эти условия, можно из уравнения движения жидкости в напряжениях получить векторное уравнение равновесия жидкости

. (2.1)

Рассмотрим наиболее часто используемый случай, когда на жидкость из массовых сил действует только сила тяжести . Напряжение этой силы, как было показано в п. 1.2, . Тогда уравнение (2.1) примет вид

,

проектируя которое на оси координат, можно получить систему трех скалярных уравнений равновесия жидкости

(2.2)

Как видно из двух первых уравнений системы (2.2), давление зависит только от координаты z, и не зависит от изменения координат x и y. Отсюда следует, что если на покоящуюся жидкость действует только сила тяжести, то гидростатические давления в любой точке горизонтальной плоскости, мысленно проведенной в одной и той же жидкости, равны между собой. Такие горизонтальные плоскости называются поверхностями равного давления, одна из них изображена на рис.6.

На этом свойстве гидростатических давлений основан принцип сообщающихся сосудов, а также принцип работы жидкостных манометров.

Рис. 6

Так как в рассматриваемом случае изменение давления вдоль осей x и y отсутствует, то есть давление зависит только от координаты z, вместо системы (2.2) можно записать одно уравнение, заменив в нем частную производную на полную:

.

Для того чтобы получить зависимость давления от координаты z, необходимо проинтегрировать это уравнение. Перепишем его в виде

и проинтегрируем, учитывая, что :

, (2.3)

где C – произвольная постоянная интегрирования.

Для ее определения используем условие на свободной поверхности жидкости, на которой действует давление верхней среды (воздуха) p₀. Если совместить плоскость X0Y cо свободной поверхностью (рис.7), то получим условие

при

Подставляя эти значения в (2.3), получим значение константы интегрирования C=p₀. Тогда получим интеграл уравнения равновесия в окончательном виде

. (2.4)

Т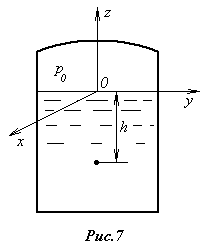 ак как нас интересует давление в произвольной точке жидкости, распо-ложенной на определенной глубине под свободной поверхностью (рис.6), то удобнее Поль-зоваться уравнением (2.4) в виде

(2.5)

Это уравнение назы-вается основным уравне-нием гидростатики, так как позволяет вычислить гид-ростатическое давление в любой точке жидкости. Здесь p – абсолютное давление в точке жидкости, p₀ – давление на свободной поверхности, gh – давление столба жидкости высотой h.

Если сосуд открыт, то давление на свободной поверхности будет равно атмосферному (p_a), и формула (2.5) примет вид

.

В гидростатике используется понятие избыточного гидростатического давления, которое показывает, на сколько абсолютное давление больше атмосферного, т. е. . Если абсолютное давление меньше атмосферного, то вводят понятие вакуума – величины, которая показывает, на сколько измеряемое давление меньше атмосферного, т. е. .