Задания для закрепления:

1. Случайная точка (X,Y) на плоскости распределена по следующему закону:

X Y	-1	0	1
0	0,10	0,15	0,20
1	0,15	0,25	0,15

Найти числовые характеристики (X,Y),

Ответ:

2. Двумерная случайная величина (X,Y) подчинена закону распределения с плотностью в области D и равна нулю вне той области. Область D - треугольник, ограниченный прямыми . Найти величину А, математические ожидания MX, MY, дисперсии DX, DY,

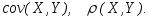
3. Ответ: ,

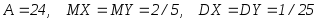3. Найти уравнение прямой и обратной регрессии для дискретной двумерной случайной величины из задания 1 настоящего параграфа, т.е. закон распределения случайной величины (X,Y) :

X Y	-1	0	1
0	0,10	0,15	0,20
1	0,15	0,25	0,15

Ответ: уравнение прямой регрессии:,

остаточная дисперсия;

уравнение обратной дисперсии: ,

остаточная дисперсия.

4. Найти уравнение прямой и обратной регрессии для дискретной двумерной случайной величины из задания 2 настоящего параграфа, т.е. двумерная случайная величина (X,Y) подчинена закону распределения с плотностью в области D и равна нулю вне той области. Область D - треугольник, ограниченный прямыми .

Ответ: уравнение прямой регрессии:,

уравнение обратной регрессии: ,

остаточные дисперсии: .

10-Занятие. Закон больших чисел. Неравенство Чебышева. Применения закона больших чисел

В широком смысле слова под «законом больших чисел» (ЗБЧ) понимают известное с глубокой древности свойство устойчивости массовых явлений, т.е. средний результат действия большого числа случайных явлений практически перестает быть случайным и может быть предсказан с достаточной определенностью.

В узком смысле слова под «законом больших чисел» понимают совокупность теорем, в которых устанавливается факт приближения средних характеристик к некоторым постоянным величинам в результате большого числа наблюдений.

Доказательств ЗБЧ основано на неравенствах Маркова и Чебышева.

Неравенство Маркова. Если случайная величина Х не принимает отрицательных значений, то для любого положительного числа

, или .

Неравенство Чебышева. Для любой случайной величины X, имеющей конечную дисперсию, и для любого числа имеет место неравенство:

,

т.е. вероятность того, что отклонение случайной величины Х от его математического ожидания МХ по абсолютной величине меньше положительного числа , не меньше чем .

Это неравенство можно записать и в другом виде: .

Применим неравенство Чебышева к последовательности случайных величин. Если - последовательность случайных величин, таких, что: 1) они попарно независимы; 2) имеют конечные дисперсии, ограниченные одной и той же постоянной С>0 (), то, каково бы ни было ,

Теорема Чебышева (Закон больших чисел). Если - последовательность случайных величин, таких, что: 1) они попарно независимы; 2) имеют конечные дисперсии, ограниченные одной и той же постоянной С>0 (), то, каково бы ни было ,

.

Если, в частности, , то

.

Содержание этой важной теоремы состоит в том, что среднее арифметическое случайных величин при достаточно большом n будет (с большой вероятностью) как угодно мало отличаться от числа или от числа а в частном случае.

Следующая теорема устанавливает связь между от относительной частотой события и его вероятностью.

Пусть произведено n независимых испытаний, в каждом из которых вероятность появления некоторого события А постоянна и равна р.

Теорема Бернулли (Закон больших чисел). При неограниченном возрастании числа независимых испытаний п относительная частота m / n появления события А сходится по вероятности к его вероятности p, т. е. каково бы ни было ,

.