5. Канонические уравнения и вариационные принципы

Во многих рассмотрениях общего характера оказывается удобным преобразовывать уравнения Эйлера к канонической форме. Это позволяет более единообразно трактовать различные классы вариационных задач физики и механики, где вводимые при таком преобразовании переменные имеют непосредственный физический смысл.

5.1 Преобразование уравнений Эйлера к каноническому виду

Будем рассматривать задачу о стационарном (или экстремальном ) значении функционала

I (44)

при некоторых границах условиях. В соответствии с п.2.7. система уравнений Эйлера для этого функционала имеет вид.

(45)

Она представляет собой систему из обыкновенных дифференциальных уравнений второго порядка с искомыми функциями

(46)

Эту систему можно заменить системой уравнений первого порядка. Введём величины

(47)

которые вместе с переменными называются каноническими переменными для функционала (44). Предположим, что из этой системы можно выразить через :

(48)

Это возможно, если якобиан системы отличен от нуля:

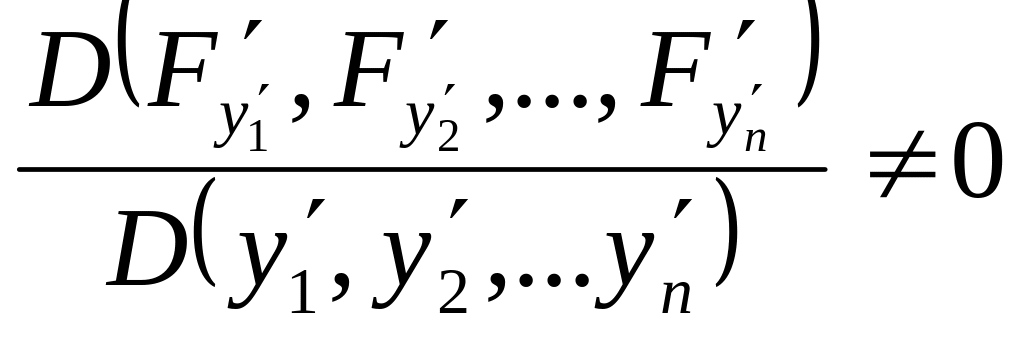
Для функционала (44) введём также функцию Гамильтона H (гамильтониан)

(49)

Дифференцируем формулу (49) и пользуясь равенст-вами (47), получим

Таким образом, если считать канонические переменные и независимыми, то

(50)

Если теперь функции (46) удовлетворяют уравнениям (45), то и второе из уравнений (50) даёт

т.е

(51)

Это и есть каноническая форма уравнений Эйлера , соответствующая функционалу (44). Она представляет собой систему из обыкновенных дифференциальных уравнений первого порядка с искомыми функциями .

Пример 21. Написать каноническую систему уравнений Эйлера для функционала

I

Решение

;

;

Отсюда находим : .

Тогда ;

Преобразуем F:

.

Тогда

Теперь получим искомую систему:

Таким образом,

5.2. Первые интегралы

Пусть дана некоторая функция

.

Если её рассматривать вдоль решения системы уравнений (51), т. е. подставить вместо независимых переменных решение этой системы, то мы получим сложную функцию , для которой

(52)

Выражение

называют скобкой Пуассона функций и и обозначается . Таким образом формулу (52) можно записать следующим образом

(53)

Отметим простые свойства скобки Пуассона без доказатель-ства, так как они почти очевидны.

1. ; 2. ; 3. ;

4. ; 5. .

Из (53) видно, в частности, что соотношение

(54)

необходимо и достаточно для того, чтобы вдоль любого решения системы (51) было

.

Таким образом, получаем первый интеграл системы (51).

Функция, сохраняющая постоянное значение вдоль каждой интегральной линии заданной системы дифференци-альных уравнений, называются первым интегралом этой системы.

Значение независимых первых интегралов позволяет понизить в системе число уравнений на .

Пусть в частности функция не зависит от . Очевидно из (49), что в этом случае и функция не зависит от . Тогда, положив , имеем .

Соотношение (54) выполняется, поэтому , в этом случае и функция постоянна вдоль любой экстремали.

Пример 22. Закон сохранения энергии.

Основным вариационным принципом в механике являются принцип стационарного действия Остроградского –Гамильтона: среди возможных, т. е. совместимых со связями, движений системы материальных точек в действительности осуществляется движение, дающее стационарное значение(т.е. значение, соответствующее аргументу, для которого вариация функционала равна нулю) интегралу ,

где -кинетическая, а -потенциальная энергия системы.

Функция в этом случае имеет вид

Это – полная энергия системы. Применим принцип стационар-ного действия. Если система консервативна (потенциальная энергия не зависит явно от времени), то уравнение Эйлера для рассматриваемого функционала имеют первый интеграл

Таким образом, полная энергия консервативной системы остаётся при движении постоянной.