5.3. Быстрое преобразование Фурье

Прямое вычисление для всех N частот по (5.2) тре­бует N² комплексных умножений и сложений, и для уме­ренно большого N, скажем для N, большего, чем 1000, это прямое вычисление связано с большими затратами машинного времени. Методы, экономящие машинное вре­мя, так же, как только что рассмотренный метод Герце­ля, используют некоторые искусственные приемы, в боль­шинстве случаев основанные на том, что сумма произве­дений может быть иногда упрощена, если сделать сложение до умножения, или на том, что комплексные операции могут быть заменены действительными опера­циями.

Общим для этих методов является то, что полное пре­образование rN точек занимает в r² больше времени, чем преобразование N точек. Поэтому, даже если метод вы­числения по выражению (5.2) требует только ¼ N² опе­раций, последовательности больше чем, скажем, из 10 000 точек потребуют невыполнимого количества вычис­лений. Однако все такие методы совсем недавно были вытеснены несколькими сходными алгоритмами, которые все вместе можно назвать быстрыми преобразованиями Фурье. Эти алгоритмы не применяются в тех случаях, когда число точек в последовательности является простым, но зато при N сложносоставном (имеющем много множителей) экономия может быть чрезвычайно большой. Когда N есть степень числа 2 (состоит из максимального числа множителей), то алго­ритмы быстрых преобразований Фурье требуют проведе­ния числа вычислений, пропорционального не N², а , что, например, при N=1024 составляет 99%-ную экономию в вычислениях. Для эффективного использования этих алгоритмов требуется, чтобы N раз­лагалось на возможно большее число множителей. В большинстве задач на преобразуемые данные можно наложить это ограничение с тем, чтобы алгоритмы быст­рого преобразования Фурье могли быть использованы.

При дальнейшем изложении будем пользоваться обо­значениями в виде индексов, принятых в (5.18) и на рис. 5.3. Будем также обозначать величину как W. Тогда (5.2) и (5.3), определяющие ДПФ, примут вид

(5.43)

и

(5.44)

Из уравнения (5.43) не следует делать вывод, что W не зависит от N. Для последовательности с N/2 точками в (5.43) не только верхний предел суммы должен стать N/2—1, но и W должно быть заменено на W².

Существуют два класса алгоритмов быстрого преоб­разования Фурье, и каждый класс имеет множество мо­дификаций. Рассмотрим сначала метод, называемый про­реживанием (decimation) по времени.

Прореживание по времени

Предположим, что число отсчетов N делится на два. Тогда полезно рассмотреть дискретные преобразования Фурье двух более коротких последовательностей: , со­стоящей только из четно пронумерованных отсчетов, и , состоящей только из нечетно пронумерованных отсчетов. Эти последовательности иллюстрируются рис. 5.6 и фор­мально задаются как

,

(5.45)

,

Дискретные преобразования Фурье для этих последова­тельностей являются также последовательностями, со­стоящими из N/2 точек, или, как было показано, могут считаться периодическими последовательностями с пе­риодом N/2.

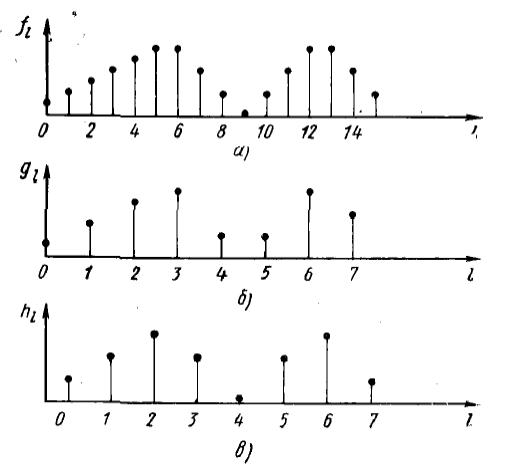
Рис. 5.6. Последовательность из шестнадцати точек (а); последова­тельность из восьми точек, образованная из четно пронумерованных отсчетов (б); последовательность из восьми точек, образованная из нечетно пронумерованных отсчетов (в).

Они могут быть записаны в виде

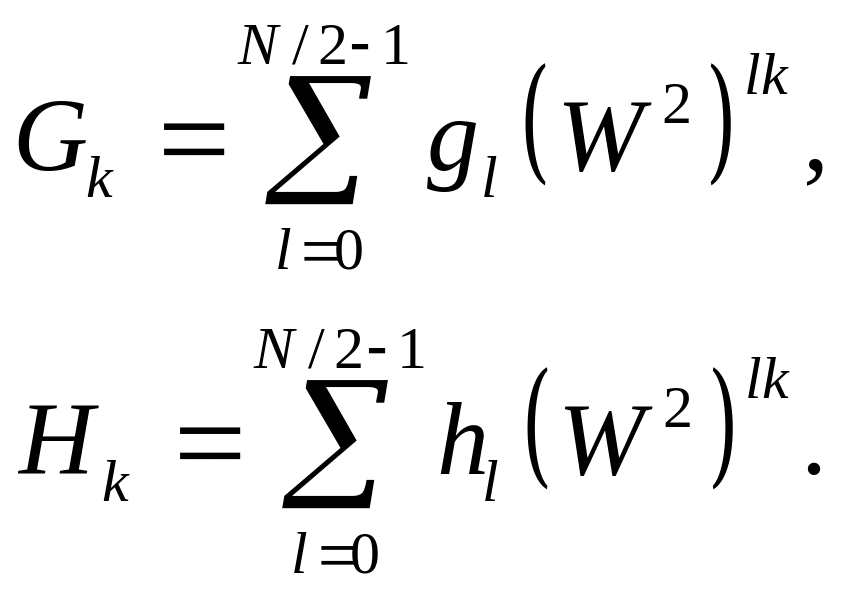(5.46)

Для нас представляет интерес ДПФ от полной последо­вательности, которое может быть выражено через и из (5.45):

. (5.47)

Простая манипуляция с выражением (5.47) дает

(5.48)

Соотношение (5.48) между F_k , G_k и H_k имеет важное значение для вычислений. В самом деле, G_k и H_k могут быть вычислены цри прямом методе с помощью (N/2)² операций каждая, а соединение их, дающее F_k , требует дополнительно проведения только N операций, что в сум­ме составляет N + N²/2 операций (под операцией здесь подразумевается комплексное умножение и сложение). Но прямое вычисление F_k требует N² операций, и по­этому (5.48) экономит вычисления почти в два раза для больших N.

В (5.48) индекс k изменяется от 0 до N—I. Однако G_k и H_k имеют период N/2 и вычисляются только в диа­пазоне от 0 до N/2—I. Поэтому необходимы особые «ре­цепты» для вычисления F_k при и при , а именно:

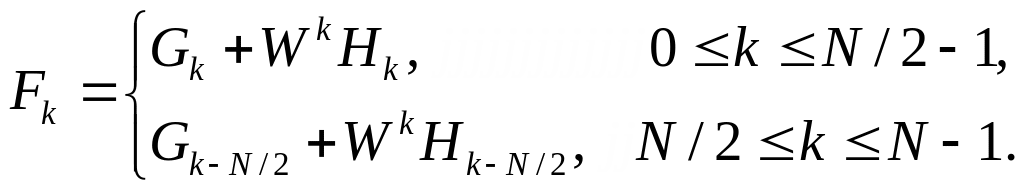(5.49)

Рис. 5.7. Восьмиточечное ДПФ, приведенное к двум четырехточечным ДПФ с помощью прореживания по времени.

Это соотношение между F_k , G_k и H_k изображено на рис. 5.7, который показывает восьмиточечное ДПФ, сведенное к двум четырехточечным (направленный сигнальный граф может быть незнаком некото­рым читателям. Основой его построения являются точки (или узлы) и стрелки (линии передачи). Каждый узел представляет переменную, а стрелки, указывающие на этот узел, берут начало в узлах, чьи переменные участвуют в формировании переменной данного узла. Это участие является аддитивным, и вес каждого слагаемого, если он отличается от единицы, обозначается постоянной, написанной ря­дом на линии передачи.

Рис. 5.8. Восьмиточечное ДПФ, приведенное к четырем двухточечным.

Так, на рис. 5.7 величина F₇ у нижнего правого узла равна G₃ +W ⁷H₃. Операции, отличные от сложения и умножения на постоянную величину, должны быть ясно обозначены символами, отличными от точки или стрелки.)

Может случиться, что N/2 также делится на 2. В этом случае, поскольку , G_k и H_k являеотся дискретными преоб­разованиями Фурье, их вычисление может быть уменьше­но тем же способом, каким было уменьшено вычисление F_k . Следуя этим путем, объем вычислений F_k можно успешно уменьшать, если все более и более увеличивать число ДПФ от все меньшего и меньшего числа точек со все большей и большей экономией вычислительных опе­раций.

В этом и заключается сущность метода быстрого преобразования Фурье, На рис. 5.8 два четырехточечных ДПФ из рис. 5.7 приведены каждое к двум двухточеч­ным, а на рис. 5.9 каждое двухточечное ДПФ приведено к двум одноточечным (которые являются нулевыми операциями, и поэтому полное вычисление F_k сводится к комплексным умножениям и сложениям).

До сих пор рассматривался только случай, когда N является степенью числа 2 или по крайней мере делится на 2. Прежде чем перейти к случаю общего N, обсудим более детально случай, когда N есть степень 2. Рассмо­трение рис. 5.9 дает значительную информацию о прак­тических аспектах вычисления дискретного преобразова­ния Фурье. Из рисунка легко видеть, что там имеется 8×3 узлов и 2×8×3 стрелок, соответствующих сложениям и умножениям. Половина умноже­ний может быть опущена, поскольку линии передачи, обозначенные стрелкой без надписи, имеют коэффициент умножения, равный единице.

Рис. 5.9. Восьмиточечное ДПФ, полностью сведенное к комплекс­ным умножениям и сложениям повторением прореживания по вре­мени (здесь требуется двоично-инверсная перестановка входных отсчетов)

Очевидно, половину остав­шихся умножений также легко исключить, если учесть, что . Поэтому, если N есть степень 2, то для вычисления ДПФ последовательности из N точек требу­ется сложений и самое большее ½ умно­жений.

Допустим, кроме того, что входные данные могут за­поминаться в памяти машины в порядке

как на рис. 5.9. Тогда вычисление дискретного преобра­зования Фурье может быть сделано «с замещением» (in place), т. е. путем записи всех промежуточных ре­зультатов на место исходной последовательности данных, а окончательного ответа — на место промежуточных ре­зультатов.

Чтобы показать это, предположим, что каждый узел соответствует двум регистрам памяти (двум, потому что величины являются в общем случае комплексными). Са­мые крайние слева восемь узлов представляют регистры, содержащие входные данные в переставленном порядке. Первая ступень вычислений заключается в вычислении содержимого регистров, представленных следующими во­семью узлами вправо от входных узлов. Но каждая пара входных узлов воздействует только на соответствующую пару узлов, находящихся непосредственно за ними спра­ва, и, если вычисления проводятся с двумя узлами одно­временно, новые вычисленные значения могут быть запи­саны в те регистры, из которых взяты входные значения, поскольку входные значения больше не будут нужны для дальнейших вычислений. На второй ступени производился вычисление величин для следующего вправо вертикального ряда узлов, также включающего пары узлов, хотя узлы в этих парах разде­лены теперь двумя позициями вместо одной. Этот факт не изменяет свойства вычисления с замещением, поскольку каждая такая пара узлов воздействует только на пару узлов, следующую непосредственно за ней справа. Поэто­му после того, как новая пара значений будет вычислена, она может быть сохранена в регистрах, где хранились старые, больше не нужные результаты, В вычислениях для последнего вертикального ряда узлов, соответствую­щих значениям дискретного преобразования Фурье, уча­ствуют пары узлов, разделенные уже четырьмя позиция­ми, но свойство замещения по-прежнему сохраняется.

Первоначальная перестановка данных в последова­тельности необходима для вычисления с применением метода замещения. Если ее не производить, то по мере развития алгоритма нечетно пронумерованные члены пе­реместятся к концу последовательности. Изменение по­рядка следования отсчетов во входной последовательно­сти получило наименование двоичной инверсии (bit reversal), поскольку отсчет, временной индекс которого дается двоичным числом должен быть сдвинут на место а отсчет, временной индекс которого дол­жен быть сдвинут на место . Заметим, что переста­новка в исходной последовательности может быть также произведена с замещением.

Из рис. 5.9 можно видеть, что два показателя степе­ни у W, требуемые для вычисления любой пары узлов, отличаются на 4 или, в общем случае, на N/2. Так как W^N/2 равно -1, то вычисления для пары узлов можно сделать с помощью всего лишь одного комплексного умножения, одного комплексного сложения и одного ком­плексного вычитания. Поэтому, если вычитание эквива­лентно по сложности сложению, то наш предыдущий подсчет операций оправдывается.

Структура рис. 5.9 поясняет основную идею замены вычисления дискретного преобразования Фурье вычисле­нием двух меньших дискретных преобразований Фурье, а каждого из этих — вычислением двух еще меньших пре­образований и т. д.

На рис. 5.9 предполагается определенное распределе­ние запоминаемых данных в памяти вычислительной ма­шины до, во время и после вычисления. Подобные вычисления с различным распределением данных изобра­жаются разного рода направленными графами, и они мо­гут зачастую оказаться вариантами алгоритмов, исполь­зующих прореживание по времени.

Например, если представить, что на рис. 5.9 все узлы на горизонтали F₁ переставлены местами со всеми уз­лами на горизонтали F₄ , а все узлы на уровне F₃ пере­ставлены местами с узлами на уровне F₆, причем стрелки перенесены вместе с узлами, то направленный граф ста­новится таким, как на рис. 5.10.

Для такого варианта-графа не нужно, чтобы исходные данные были подверг­нуты двоичной инверсной перестановке, однако результирующий спектр оказывается переставленным. Дополни­тельным неудобством может быть то, что степени у W, необходимых для проведения вычислений, располагаются в двоично-инверсном порядке. Первоначальное описание алгоритма, принадлежащее Кули , соответствует на­правленному графу рис. 5.10.

Несколько более сложное видоизменение рис. 5.9 приводит к сигнальному направленному графу рис. 5.11. В этом случае как входные данные, так и результирую­щий спектр представлены в «естественном» порядке, и коэффициенты в вычислениях также употребляются в естественном порядке. Однако вычисления теперь не могут производиться с замещением. Поэтому должен быть предусмотрен по крайней мере еще один дополнительный набор регистров. Этот сигнальный направленный граф и соответствующая ему процедура вычислений раз­работаны Стокхемом и независимо от него Санди.

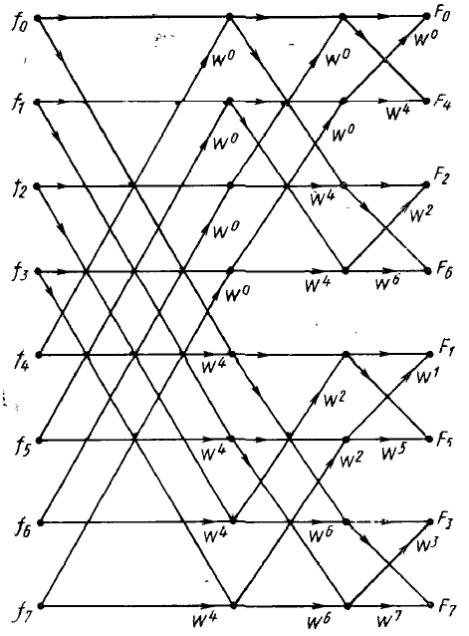
Рис. 5.10. Видоизменение рис. 5.9, дающее алгоритм с нормальной нумерацией входной последовательности, но с двоично-инверсной перестановкой номеров выходной последовательности и коэффициентов.

Приведенные три формы сигнального направленного графа имеют смысл в том случае, когда данные хранятся в памяти с произвольной выборкой. Иногда данных слиш­ком много, чтобы держать их в памяти одновременно.

В этом случае используется вспомогательная память с возможностью последовательной выборки. Остановимся на видоизменении рис. 5.9, соответствующем алгоритму Синглетона. Структура этого графа от участка к уча­стку остается одной и той же и требует последователь­ного выбора данных из четырех раздельных массивов. Поэтому для практического применения алгоритма, изо­браженного на рис. 5.12, необходимы четыре магнитофона или магнитный барабан по крайней мере с четырьмя ка­налами.

До сих пор детально рассматривался только случай, когда N делится на 2. Все, что при этом делалось, может быть обобщено и на случай других делителей, однако алгоритмам при N, не являющимся степенью числа 2, уделялось меньше внимания. Это объясняется двоичной организацией цифровых вычислительных машин и тем, что при таких N и возрастающих количествах входных данных становится все труднее составлять программы. Тем не менее, если N имеет множитель p, можно сформи­ровать p различных последовательностей , заданных в виде

(5.50 а)

и имеющих N/p точек. Индекс (i) здесь обозначает i-ю последовательность, а не показатель степени. Каждая из этих последовательно­стей имеет ДПФ G_k⁽ⁱ⁾ и ДПФ от f_п может быть вычислено с помощью p более простых ДПФ с pN комплекс­ных умножений и сложений, т. е.

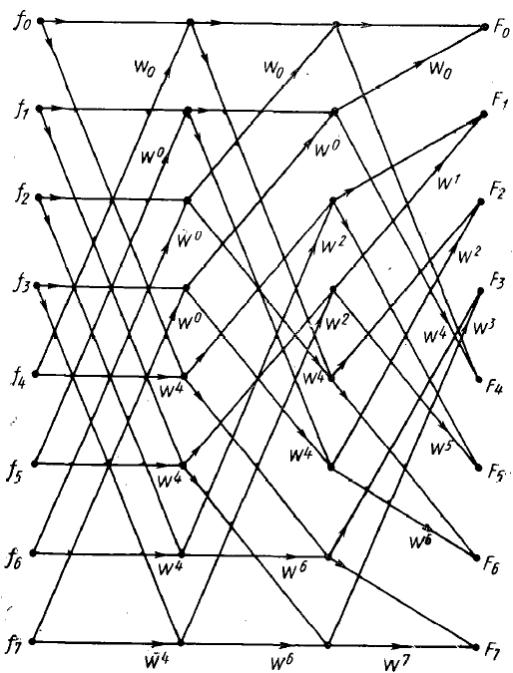
Рис. 5.11. Видоизменение рис. 5.9, которое уничтожает необходи­мость в двоично-инверсной перестановке, но не допускает вычисле­ния преобразования с замещением.

Рис. 5.12. Видоизменение рис. 5.9 с постоянной структурой на всех участках

Алгоритм требует, чтобы входные данные были представлены в двоично-инверсном порядке, но степени W необходимо располагать в естественном порядке.

для (5.50 б)

что совпадает с (5.49), если p = 2. На рис. 5.13,а изо­бражен случай, когда p = 3 и N = 6, а на рис. 5.13,б —слу­чай, когда p = 2, N = 6. Если N/p является составным, то вычисления различных G_k⁽ⁱ⁾ могут быть затем снова упрощены. Общей для рассмотренного выше набора методов является процедура формирования подпоследовательностей из преобразуемой последовательности, причём каждая подпоследовательность составляется только из каждой р-й точки исходной последовательности.

Это мож­но понимать так, словно подпоследовательности образуются путем дискретизации временной функции с меньшей частотой или путем пропуска р-1 отсчетов из каждой группы в p отсчетов; отсюда и происходит название «прореживание по времени».

Рис. 5.13. Прореживание по времени:

а) для шеститочечного ДПФ с р=3;

б) для шеститочечного ДПФ с р=2.