2.12. Цепи для разностного уравнения второго порядка

Разностное уравнение второго порядка

(2.32)

соответствует цепи, изображенной на рис. 2.14.

Z-преобразование для (2.32) выражается формулой

(2.33)

Цепь с характеристикой имеет нуль и два полю­са. Из рис. 2.14 можно видеть, что нуль формируется элементами задержки в прямой ветви, т. е. задержкой входного сигнала, в то время как полюсы формируются задержками в ветви обратной связи с выхода.

Рис. 2.14 Прямая форма цифровой цепи с двумя полюсами и одним нулем

Другая эквивалентная цель с характеристикой может быть получена путем перестановки местами прямой ветви и ветви обратной связи, как это показано на рис. 2.15.

Третья цепь с характеристикой , эквивалентная цепям на рис. 2.14 и 2.15, показана на рис. 2.16. Этот вариант легко получается из рис. 2.15, если обратить вни­мание на то, что крайний справа элемент задержки на рис. 2.15 является лишним, так как на его вход поступает тот же сигнал, что и на первый элемент задержки.

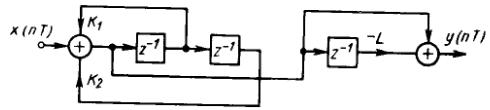
Рис. 2.15 Другая форма цифровой цепи с двумя полюсами и одним нулем

Рис. 2.16 Каноническая форма цепи с двумя полюсами и одним нулем

Рис. 2.17 Связанная форма двухполюсной цепи

Цепь рис. 2.16 называется канонической, потому что в ней задержки используются для формировании и ну­лей, и полюсов, и, таким образом, эта система имеет минимальное число элементов задержки для цепи дан­ного порядка, т. е. n задержек для цепи n-го порядка Ниже будет показано, что, хотя все схемы от рис. 2.14 до рис. 2.16 производят идентичные z-преобразования, их поведение при наличии шума, вызванного ошибкой округления при умножении, различно.

Еще одна реализация системы второго порядка с двумя полюсами показана на рис. 2.17. Эта цепь описывается системой двух уравнений:

(2.34)

Можно взять z-преобразования обоих уравнений и за­тем получить явные выражения для и :

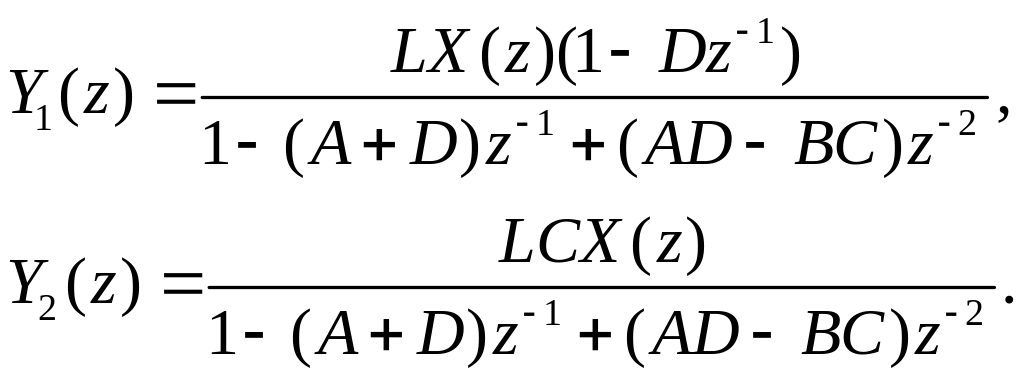(2.35)

Легко установить, что и соответствуют цепям с полюсами, имеющими радиальное расстояние от центра единичной окружности и углы, равные . Выражение имеет двукратный нуль в точке , а имеет два нуля на действительной оси в точках и . Таким обра­зом, выходные сигналы и полностью со­впадают с аналогичными сигналами в ранее описанных, системах второго порядка. Эта система кажется более сложной, так как требуется выполнять четыре операции умножения вместо двух или трех, но, тем не менее, она представляет интерес. Как будет показано в гл. 4, до­полнительные возможности для выбора параметров ча­сто бывают полезными при расчете фильтра, когда стремятся уменьшить вредное влияние квантования парамет­ров, с тем чтобы уменьшить длину слова при аппаратурной реализации.

Из описанных цепей можно составить более сложные системы путем образования из них последовательной, параллельной или смешанной (последовательно-параллельной) комбинаций. Например, два уравнения

(2.36)

соответствуют последовательному включению (рис. 2.18,а), поскольку сигнал на выходе цепи, описы­ваемой первым уравнением, используется а качестве входного сигнала цепи, описываемой вторым уравнением. Аналогично, уравнения

(2.37)

соответствует параллельному включению, представлен­ному на рис. 2.18,б. Последовательное соединение цифровых цепей обеспечивает естественную развязку одной пели от другой, в отличие от непрерывных систем, где требуются специальные и противоестественные разделительные усилители, предотвращающие взаимодействие между соседними RLC-цепями. Это объясняет до некоторой степени, почему при расчете RLC-цепей особое вни­мание уделяется физической реализации, что, в свою очередь, вызвало необходимость создания весьма изящной и довольно сложной теории синтеза. Такая теория пред­ставляется ненужной для расчета дискретных фильтров.

Рис. 2.18 Последовательная или каскадная (а) и параллельная (б) формы цифровых цепей