5.2. Основы алгебры логики

Математической основой цифровых логических устройств является двоичная алгебра, в которой используются всего два числа — 0 и 1. Выбор двоичной системы счисления диктовался требованиями простоты технической реализации самых сложных задач с использованием всего одного базового элемента — ключа, который имеет два состояния: включен (замкнут) и выключен (разомкнут). Если первое состояние ключа принять за условную (логическую) единицу, то второе будет отражать условный (логический) ноль или наоборот.

Одни и те же преобразования логических переменных можно задать в различных формах: с помощью операций И, ИЛИ, НЕ (булевский базис), операции И–НЕ (базис Шеффера), операции ИЛИ–НЕ (базис Пирса), а также многими другими способами. Выбор базиса зависит от простоты реализации той или иной операции с помощью электрических схем данной схемотехнологии. Чаще всего используют базисы Шеффера и Пирса. В развитых сериях стандартных ИС наряду с базовыми логическими элементами обычно имеется и ряд других, выполняющих другие логические операции.

Проектирование цифрового устройства начинается с представления его в виде некоторого «черного ящика», в котором имеется n входов (x₁, x₂, …, x_n) и m выходов (y₁, y₂, …, y_m). Так как операции цифровой обработки информации сводятся к реализации функциональных зависимостей y_i=f(x₁, x₂, …, x_n), ставящих в соответствие каждой комбинации двоичных переменных x₁…x_n значение двоичной переменной y_i, то функционирование цифровых устройств удобно представлять в виде таблиц переключательных функций (таблиц истинности). В таких таблицах в одной части (левой) представляются переменные x, называемые аргументами, а в другой части (правой) — переменные у — функции, причем в одной таблице могут приводиться несколько функций одних и тех же аргументов. Аналитическая форма описания такой таблицы есть булева функция (по имени создателя алгебры логики Дж. Буля). Алгебра логики или булева алгебра есть раздел математики, изучающий закономерности и взаимосвязи между простыми высказываниями, образующими сложные высказывания. При этом алгебру логики не интересует информация, которую несет то или иное высказывание. С точки зрения алгебры логики важно лишь, что любое простое высказывание может быть либо истинным, либо ложным, т. е. принимать только два значения. На основе простых высказываний можно построить сложные, истинность или ложность которых находится в определенной связи от истинности или ложности простых высказываний. Эти зависимости и называют булевыми функциями. Как и в других разделах математики, в алгебре логики существуют свои теоремы, функции и математические преобразования. Так как сложные высказывания снова могут быть либо истинными, либо ложными, булевы функции тоже могут иметь лишь два значения. Если истинности приписать значение 1, а ложности 0, то окажется, что все аргументы и функции в алгебре логики, как и в цифровых устройствах, могут принимать только два значения: 1 и 0, и над этими переменными можно производить действия, называемые логическими операциями. Переход от логики работы практически любого цифрового устройства к соответствующим булевым функциям несложен, а дальнейшие преобразования позволяют достаточно просто синтезировать требуемое цифровое устройство.

Над переменными в булевой алгебре можно производить только три действия: дизъюнкцию (логическое сложение), конъюнкцию (логическое умножение) и инверсию (логическое отрицание), которые можно реализовать, используя три типа логических элементов: ИЛИ, И, НЕ.

Дизъюнкцией событий x_i называют событие y, которое состоит в наступлении одного из событий x_i или нескольких событий x_i одновременно (ИЛИ событие x₁, ИЛИ событие x₂, …, ИЛИ событие x₁+x₂+…). Иными словами, смысл операции дизъюнкции (логического сложения) заключается в том, что сложное высказывание истинно, если истинно хотя бы одно из составляющих его простых высказываний.

Функцию логического сложения математически записывают в виде

y=x₁+x₂+… или y=x₁x₂…,

где x₁, x₂, … — логические переменные, которые могут иметь только два значения: 1 или 0.

Таблица 5.1

Таблица истинности операции ИЛИ

x1	x2	y	Обозначение
0 1 0 1	0 0 1 1	0 1 1 1

Логический элемент ИЛИ, реализующий операцию логического сложения, имеет несколько входов и один выход. Сигнал логической единицы появляется на его выходе в том случае, если хотя бы на один из входов подан сигнал, соответствующий единице.

На структурных схемах логический элемент, выполняющий функцию ИЛИ, обозначают в виде прямоугольника с символом 1 внутри него.

Таблица истинности операции ИЛИ для двух аргументов и условное обозначение логического элемента, выполняющего операцию ИЛИ, представлены табл. 5.1 (существуют таблицы истинности для трех, четырех и т. д. аргументов).

Конъюнкцией событий x_i называют событие y, которое состоит в одновременном наступлении всех событий x_i (И событие x₁, И событие x₂, И ..., И событие x_n). Иными словами, смысл операции конъюнкции (логического умножения) заключается в том, что сложное высказывание истинно только в том случае, если истинны все составляющие его простые высказывания.

Функцию логического умножения математически записывают в виде

Таблица 5.2

Таблица истинности операции И

x1	x2	y	Обозначение
0 1 0 1	0 0 1 1	0 0 0 1

y=x₁x₂… или y=x₁x₂….

Логический элемент И, реализующий операцию логического умножения, также имеет несколько входов и один выход. Сигнал логической единицы появляется на его выходе только в том случае, если на все входы поданы сигналы, соответствующие единице. Поэтому логический элемент И часто называют схемой совпадений.

На структурных схемах логический элемент, выполняющий функцию И, обозначают в виде прямоугольника, внутри которого имеется символ &.

Таблица истинности операции И для двух аргументов и условное обозначение логического элемента, выполняющего операцию И, представлены табл. 5.2.

Инверсией (логическим отрицанием) события x называют событие y, противоположное событию x (событие y НЕ событие x). Иными словами, смысл операции инверсии (логического отрицания) заключается в том, что сложное высказывание истинно, когда определенное высказывание ложно, и, соответственно, ложно, когда это высказывание истинно.

Операция логического отрицания записывается в виде черточки над аргументом

и читается так: «y равно НЕ x».

Логический элемент НЕ, реализующий операцию логического отрицания, имеет один вход и один выход. Сигнал логической единицы появляется на его выходе тогда, когда на вход подан сигнал, соответствующий логическому нулю. В соответствии с выполняемой операцией инверсии элемент НЕ называют инвертором.

Таблица 5.3

Таблица истинности операции НЕ

x	y
1 0	0 1

Выполняется эта операция над одной переменной, таблица истинности операции НЕ приведена в табл. 5.3. Инверсия по выходу (входу) обозначается кружком (○) у выхода (входа) на контуре прямоугольника, изображающего логический элемент.

Рассмотренные правила выполнения логических операций можно использовать для выполнения более сложных логических преобразований. Учитывая правила выполнения операции ИЛИ, получаем следующие соотношения для произвольной логической переменной x:

x+0=x; x+1=1; x+x=x;

Применяя правила выполнения операции И, получаем

x0=0; x1=x; xx=x;

Эти четыре пары соотношений называют соответственно законами нулевого множества, универсального множества, повторения (тавтологии), дополнительности.

Из правила выполнения инверсии следует, что

— закон двойной инверсии.

Кроме того, для двух и более переменных справедливы следующие законы булевой алгебры:

переместительный

x₁+x₂=x₂+x₁; x₁x₂=x₂x₁;

сочетательный

x₁+x₂+x₃=x₁+(x₂+x₃)=(x₁+x₂)+x₃)=(x₁+x₃)+x₂; x₁x₂x₃=x₁(x₂x₃)=(x₁x₂)x₃)=(x₁x₃)x_2.;

распределительный

x₁(x₂+x₃)=x₁x₂+x₁x₃; x₁+x₂x₃=(x₁+x₂)(x₁+x₃)

(вторая форма специфична и справедлива только в булевой алгебре);

обращения

если x₁=x₂, то

поглощения

x₁+x₁x₂=x₁; x₁(x₁+x₂)=x₁;

склеивания

де Моргана

Таблица 5.4

Таблица истинности операции ИЛИ–НЕ

x1	x2	y
0 1 0 1	0 0 1 1	1 0 0 0

Перечисленные законы используют при преобразованиях логических функций. При этом вводится важное понятие о функционально полной системе — таком наборе логических элементов, с помощью которого можно реализовать любую логическую функцию.

Поскольку любая логическая функция представляет собой комбинацию логических операций сложения, умножения и отрицания, набор логических элементов трех типов (ИЛИ, И, НЕ), очевидно, является функционально полным. Однако это не единственный функционально полный набор. В алгебре логики доказано, что функционально полных систем много и среди них есть такие, которые состоят всего из одного типа логических элементов, реализующих логические операции, отличные от простейших. В частности, такими функционально полными являются системы, реализующие логические операции ИЛИ–НЕ отрицания логического сложения (стрелка Пирса, y=x₁x₂) и И–НЕ отрицания логического умножения (штрих Шеффера, y=x₁x₂).

Операция ИЛИ–НЕ характеризует сложное высказывание, которое истинно только тогда, когда ложны все простые высказывания, и ложно, когда истинно хотя бы одно простое высказывание. Таблица истинности операции ИЛИ–НЕ для двух аргументов представлена в табл. 5.4, а условное обозначение реализующего ее элемента — на рис. 5.3, а.

Для доказательства того, что стрелка Пирса является функционально полной системой, обратимся к рис. 5.3, где показаны схемы инвертора, дизъюнктора и конъюнктора, выполненных на одном типе логических элементов (ИЛИ–НЕ). Схема на рис. 5.3, б представляет собой инвертор, так как в соответствии с законом тавтологии при объединении входов логического элемента ИЛИ–НЕ получим , т. е. . Для выполнения операции дизъюнкции (логического сложения) необходимо последовательно включить два элемента ИЛИ–НЕ, причем второй в режиме инвертора (рис. 5.8, в). Наиболее сложно с помощью элементов ИЛИ–НЕ реализуется операция конъюнкции, когда надо использовать три элемента (рис. 5.3, г). Так как все три основные логические операции реализуются с помощью элемента ИЛИ–НЕ, следовательно, этот логический элемент один позволяет реализовать любую сколь угодно сложную логическую функцию, т. е. он является функционально полным.

Рис. 5.4. Цифровые схемы на логическом элементе И–НЕ: а — условное обозначение; б — инвертор; в — схема реализации операции конъюнкции; г — схема реализации операции дизъюнкции

Таблица 5.5

Таблица истинности операции И–НЕ

x1	x2	y
0 1 0 1	0 0 1 1	1 1 1 0

Операция И–НЕ характеризует сложное высказывание, которое истинно только тогда, когда ложно хотя бы одно простое высказывание, и ложно, когда истинны все простые высказывания. Таблица истинности операции И–НЕ для двух аргументов представлена в табл. 5.5, а условное обозначение реализующего ее элемента — на рис. 5.4, а.

Рис. 5.3. Цифровые схемы на логическом элементе ИЛИ–НЕ: а — условное обозначение; б — инвертор; в — схема реализации операции дизъюнкции; г — схема реализации операции конъюнкции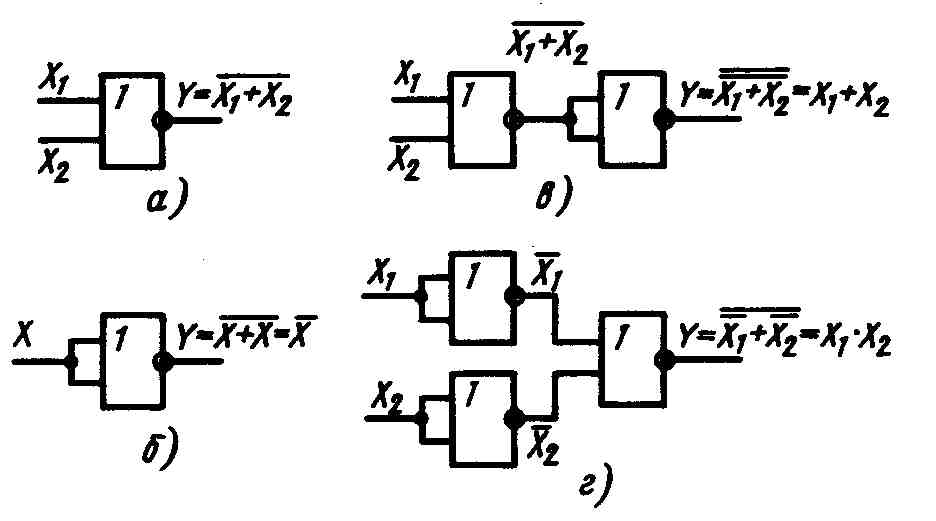

Для доказательства того, что штрих Шеффера является функционально полной системой, обратимся к рис. 5.4, где показаны схемы инвертора, конъюнктора и дизъюнктора, выполненных на одном типе логических элементов (И–НЕ). Схема на рис. 5.4, б представляет собой инвертор, так как в соответствии с законом тавтологии при объединении входов логического элемента И–НЕ имеем , т. е. . Для выполнения операции конъюнкции нужно последовательно включить два элемента И–НЕ, причем второй элемент в режиме инвертора (рис. 5.4, в). Наиболее сложно с помощью элементов И–НЕ реализуется операция дизъюнкции, когда надо использовать три элемента (рис. 5.4, г). Так как все три основные логические операции реализуются с помощью элемента И–НЕ, следовательно, и этот элемент позволяет реализовать любую сколь угодно логическую функцию, т. е. он является функционально полным.

Однако то обстоятельство, что один логический элемент (ИЛИ–НЕ или И–НЕ) составляет функционально полную систему, не означает, что на практике нужно ограничиваться только одним логическим элементом. При проектировании одних устройств может оказаться более удобным элемент ИЛИ–НЕ, а при проектировании других — элемент И–НЕ. Например, как следует из рис. 5.3 и 5.4, даже при реализации дизъюнктора и конъюнктора один из элементов оказывается предпочтительнее другого.

На практике с целью сокращения номенклатуры элементов пользуются не функционально полной системой элементов И, ИЛИ, НЕ, а системой, включающей только два элемента, выполняющих операции И–НЕ и ИЛИ–НЕ, или даже один из этих элементов. Причем число входов этих элементов, как правило, задано.

Для синтеза логических устройств в заданном базисе логических элементов используют два технических приема: двойное инвертирование исходного выражения или его части и применение теоремы де Моргана. Если требуется привести логического уравнения к базису логических элементов И–НЕ, то указанными приемами уравнение преобразуют к виду, содержащему только операции логического умножения и инверсии. При необходимости приведения логического уравнения к базису логических элементов ИЛИ–НЕ указанными приемами уравнение преобразуют к виду, содержащему только операции логического сложения и инверсии.

Для логических элементов ИЛИ–НЕ сигнал логической единицы хотя бы на одном входе однозначно определяет получение на выходе сигнала логического нуля. По аналогии, для логических элементов И–НЕ сигнал логического нуля хотя бы на одном входе однозначно определяет получение на выходе сигнала логической единицы. Значение логической переменной, которое однозначно определяет выходной сигнал логического элемента, называют активным логическим уровнем. Очевидно, что для логических элементов ИЛИ–НЕ активным логическим уровнем является сигнал логической единицы, а для логических элементов И–НЕ — сигнал логического нуля.

Из сказанного следует, что уменьшить фактическое число входов логических элементов можно, подавая на неиспользуемые входы сигналы пассивных логических констант: 0 — для элементов ИЛИ–НЕ, 1 — для элементов И–НЕ.