Дискретные ограничения с неравенствами

Учет ограничений типа неравенств в задаче дискретной оптимизации (S_D S_H) незначительно усложняет процедуру случайного поиска. В этом случае к условиям (15.4.7) добавляется еще одно условие C[N+1] S_H , которое легко проверяется.

23.3. Алгоритмы структурной оптимизации

Задача автоматического проектирования включает в себя и определение структурных факторов. Они могут быть определены в процессе решения оптимизационной задачи (15.1.5) Для этого необходимо построить процесс поиска оптимальной структуры W. Такого рода процесс поиска можно осуществить двояким образом - дискретизацией структуры и путем ее эволюционной оптимизации.

Дискретизация структуры

Если структура образуется набором структурных элементов, то ее удобно кодировать двоичным вектором

W=( ₁, ..., _n), (23.18)

где _i характеризует наличие ( _i=1) или отсутствие ( _i=0) i-го структурного элемента в проектируемой САУ. На вектор W могут быть наложены ограничения типа равенств и неравенств, характеризующие зависимость между структурными элементами. Тогда задача проектирования САУ сводится к решению следующей оптимизационной задачи:

(23.19)

где ограничения S имеют вид

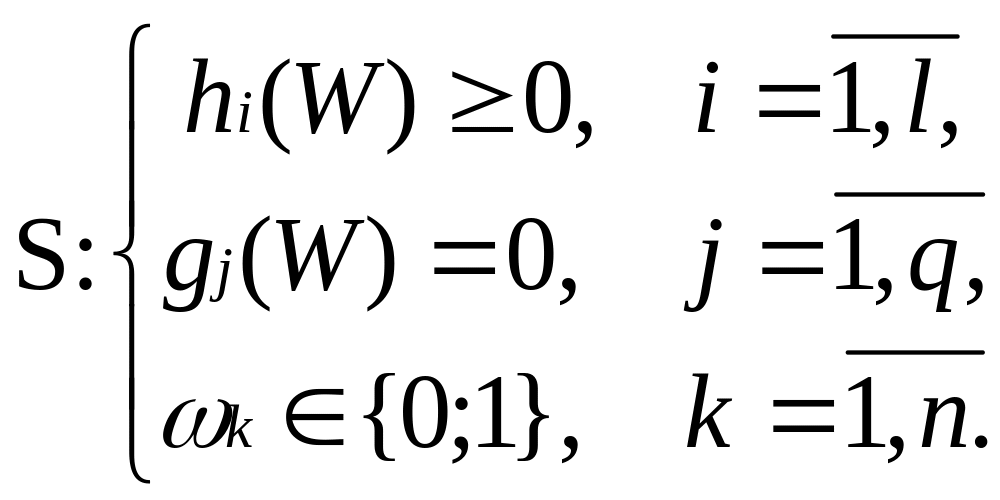(23.20)

Здесь функционалы Q, g_j и h_i определяются характером задачи проектирования конкретной САУ.

Как видно, задача проектирования сведена к задаче бинарного программирования, решение которой при малых n возможно полным перебором, а при больших - путем сведения дискретной задачи к непрерывной и дальнейшим решениям ее методами параметрического поиска, рассмотренными выше. Сделать это можно, например, введением штрафной функции вида :

(23.21)

где v>0 - коэффициент штрафа, а область S` определена условиями

(23.22)

где w_h - непрерывный параметр. Задача имеет многоэкстремальный характер и решается глобальными методами.

Другим способом сведения дискретной задачи (15.7.2) и непрерывной является рандомизация, в соответствии с которой вводится непрерывный вектор вероятностей

P=P₁, ..., P_n), (23.23)

в котором

P_k=P{w_k=1} (23.24)

-вероятность события w_k=1. С помощью этого вектора функционал Q(W) сглаживается:

(23.25)

где суммирование проводится по всем вариантам двоичного вектора—и введены обозначения

(23.26)

Сглаженный (или рандомизированный) функционал Q(W) зависит лишь от непрерывного вектора вероятностей Р. Легко видеть, что минимум этого функционала лежит в одной из вершин гиперкуба {P}, т.е. решение P_оп является двоичным вектором, который совпадает с решение исходной задачи. Для приближенной оценки значения сглаженного функционала при заданном Р можно воспользоваться методом Монте-Карло:

(23.27)

где N база оценки, а W_i случайный двоичный вектор распределения Р. С ростом N точности оценки естественно возрастает.