1.21. Понятие гармонической функции.
Функция называется гармонической в области V, если эта функция имеет непрерывные частные производные до второго порядка включительно во всех внутренних точках области V и удовлетворяет в этой области уравнению Лапласа ΔU(x,y,z)=0. Точно так же определяется понятие гармонической функции u(x,y) для плоской области D. Примером такой функции в пространстве служит функция
не зависит от сферических координат оператор Лапласа
для этой функции имеет вид
является гармонической функцией во всем пространстве, кроме начала координат. Точно так же убеждаемся, что функция
является
гармонической функцией на всей плоскости,
кроме точки 
Функция
и
называются фундаментальным решением
уравнения Лапласа соответственно в
пространстве и на плоскости. Эти функции
играют большую роль в теории гармонических
функций.
Функция Грина. Решение задачи Дирихле
с помощью функции Грина
1. Случай пространственной области.
Пусть
требуется найти функцию 
удовлетворяющую внутри области V уравнению
граничному
условию 
Для решения этой задачи введем понятие функции Грина для
области V. Функцией Грина задачи Дирихле называется функция
где
– расстояние между точками 
– гармоническая по переменным 
в области V
функция, удовлетворяющая граничному
условию
Таким
образом, функция Грина является
гармонической функцией в области V
по переменным 
кроме точки 
,и
удовлетворяет граничному условию
Пусть
функция 
-
решение задачи .
Тогда интегральное представление этой функции в силу
имеет вид
Если же функция - решение неоднородной задачи, то ее интегральное представление имеет вид
Таким образом, чтобы найти решение задачи Дирихле для уравнений Лапласа и Пуассона, достаточно знать функцию Грина для данной области V.
2. Случай плоской области.
Аналогичном
строится функция Грина для плоской
области. Пусть D-
область на плоскости xOy,
ограниченная контуром C,
-
внутренняя точка, 
-произвольная
точка область D.
Функцией Грина задачи Дирихле для
области D
называется функция 
функция,
гармоническая в области D
по переменным 
,
удовлетворяющая граничному условию
области
D,
кроме точки M0(x,y)
и удовлетворяет граничному условию
Если
функция 
удовлетворяет в области D
уравнению Лапласа
и граничному условию
Тогда
Функция
u
Удовлетворяющее граничному условию , то
Отметим, что в построении функции Грина в обоих случаях участвует фундаментальное решение уравнения Лапласа.
Построение функции Грина для полупространства. Решение задачи Дирихле для полупространства.
Пусть
область V-
полупространство z>0.
Границей этой области является плоскость
z=0.
Пусть 
относительно
плоскости z=0,
,
где 
,
произвольная точка области V.
Рассмотрим функцию
где
=
=
гармонична по переменным
во всех точках области V,
кроме точки 
удовлетворяет условию 
Следовательно, функция
Является функцией Грина задачи Дирихле для полупространства. С помощью функции Грина запишем решение задачи Дирихле для уравнения Лапласа в полупространстве
Для
этого найдем 
z=0
является направлением, противоположным
оси Oz,
то есть 
.
Поэтому имеем
Далее получим
Запишем решение задачи Дирихле для уравнения Лапласа в полупространстве в цилиндрической системе координат.
Пусть в цилиндрической системе координат
Тогда 
По
теореме Пифагора 
=
+
.
По теореме косинусов 
следовательно,
Таким образом, в цилиндрической системе координат решение имеет вид
Интеграл, стоящий в правой части формул, называется интегралом Пуассона.
Построение функции Грина для полуплоскости.
Решение задачи Дирихле для полуплоскости.
Пусть
D-
полуплоскость y>0
на плоскости xOy.
Построим на плоскости точки 
Функция
гармонична
по 
во всех точках полуплоскости y>0,
кроме точки 
Поэтому функция 
является функцией Грина для полуплоскости
y>0.
Если функция u(x,y) при y>0 удовлетворяет уравнению Лапласа
и граничному условию
то
Направление внешней нормали n противоположно направлению оси Oy, поэтому
Следовательно,
Интеграл правой части формулы также называется
интегралом Пуассона.
Построение функции Грина для шара.
Решение задачи Дирихле для шара
Пусть
V-
шар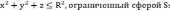 
решение
задачи Дирихле для шара проще провести
в сферической системе координат. Пусть
-внутренняя
точка шара, отличная от полюса,
Точка
называется точке 
относительно
cферы(или
окружности) радиуса R,
если эти точки лежат на одном луче,
выходящем из полюса, и если 
.
Если 
Рассмотрим функцию
Функция
гармонична по координатам точки М во
всех точках пространства, кроме точки
функция 
гармонична всюду, кроме точки
.
Поэтому функция 
гармонична по координатам точки М во
всех точках шара, кроме точки
.
По
теореме косинусов 
,
где 
,
Поэтому
Следовательно, функция
является функцией Грина задачи Дирихле для шара. направлением возрастания полярного радиуса p. Поэтому
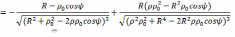
Пусть
теперь функция 
–решение
уравнения
Удовлетворяет граничному условию
Учитывая, что в сферической системе координат
получаем, что
В
этой формуле 
необходимо выразить через сферические
координаты точек 
Построение функции Грина для круга.
Решение задачи Дирихле для круга.
Пусть
D-
круг 
решение задачи Дирихле в круге будем искать в полярных
координатах
точек на плоскости. Пусть 
-
внутренняя, 
произвольная точка круга.
Рассмотрим функцию
где
-
точка, сопряженная точке 
Функция
гармонична по переменным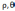
во всех точках круга, кроме точки 
.
Если 
,
то 
и 
поэтому
Следовательно, функция
является функцией Грина задачи Дирихле для круга. Так же, как в случае шара, находим, что
Теперь
решение уравнения 
удовлетворяющее граничному условию
дуги окружности 
Интеграл в правой части формулы также называется интегралом Пуассона.