Преобразованная матрица стандартизованных рангов

Показатели	Специалисты										Ri	i		i
	1	2	3	4	5	6	7	8	9	10
1	3,5	2	5,5	1	4,5	2	6	1	5,5	2	33	-2	4	0,16
2	5	1	3,5	4	2	1	3,5	2,5	3,5	1	27	-8	64	0,13
3	6	4	5,5	2,5	6	4	5	2,5	5,5	3	44	9	81	0,21
4	1	6	1,5	6	2	6	1	6	2	6	37,5	2,5	6,25	0,18
5	2	4	3,5	5	4,5	4	2	5	3,5	4,5	38	3	9	0,18
6	3,5	4	1,5	2,5	2	4	3,5	4	1	4,5	30,5	-4,5	20,25	0,15
Тj	0,5	2	1,5	0,5	0,5	2	0,5	0,5	1	0,5	210	35	184,5

Коэффициент конкордации W=0,11; критерий Пирсона хи-квадрат ²_расч = 5,59 меньше табличного значения ²_табл = 11,07 при уровне значимости  = 0,05. Следовательно, согласованность оценок экспертов низкая. Рассчитаем парные коэффициенты ранговой корреляции Спирмена:

Ранговая корреляция Спирмена
эксперты	2	3	4	5	6	7	8	9	10
1	-0,58	0,61	-0,60	0,39	-0,58	0,72	-0,74	0,52	-0,75
2		-0,51	0,52	-0,03	1,00	-0,62	0,80	-0,44	0,95
3			-0,61	0,84	-0,51	0,79	-0,79	0,98	-0,67
4				-0,41	0,52	-0,96	0,87	-0,49	0,57
5					-0,03	0,53	-0,41	0,83	-0,20
6						-0,62	0,80	-0,44	0,95
7							-0,96	0,70	-0,72
8								-0,72	0,88
9									-0,61

Оценки 1, 3, 5, 7 и 9-го экспертов согласованы. Оценки 2, 4, 6 и 8-го экспертов также согласованы. Необходимо провести обработку экспертных оценок и проверку их согласованности по группам:

1 группа	Абсолют. значения		Относит. значения	2 группа	Абсолют. значения	Относит. значения
объект1	25		0,24	объект1	8	0,08
объект2	17,5		0,17	объект2	9,5	0,09
объект3	28		0,27	объект3	16	0,15
объект4	7,5		0,07	объект4	30	0,29
объект5	15,5		0,15	объект5	22,5	0,21
объект6	11,5		0,11	объект6	19	0,18
W = 0,74		КОЭФФИЦИЕНТ КОНКОРДАЦИИ				W = 0,814
χ2=18,58		КРИТЕРИЙ ПИРСОНА ХИ-КВАДРАТ				χ 2= 20,36

Для 5%-ного уровня достоверности  (вероятность ошибки), при ν = m - 1 = 4 степенях свободы (число оцениваемых факторов без одного) величина ² = 9,488 (см. табл. 5), то есть ²_расч > ²_табл. Следовательно, полученная ранжировка статистически значима. Поэтому с вероятностью 95% можно утверждать, что имеется неслучайная согласованность мнений экспертов по ранжировке оцениваемых параметров.

Корреляционно-регрессионный анализ

Корреляционно-регрессионный анализ применяется для определения и выражения формы аналитической зависимости результативного признака y от факторных признаков x_i и измерению тесноты корреляционной связи. Основу решения первой задачи корреляционно-регрессионного анализа составляет качественный анализ данной зависимости. Математическим средством ее количественного выражения является метод наименьших квадратов: сумма квадратов отклонений расчетных значений y_р, т.е. полученных из выбранного уравнения связи, от фактических значений y_ф должна быть минимальной

S =  (y_р - y_ф)²  min. (4)

При расчете параметров уравнения регрессии для линейной формы связи типа

у = а₀ + а₁х₁ + а₂х₂ + а₃х₃ + а₄х₄

решается система нормальных уравнений:

 y =   а₀ + а₁х₁ + а₂ х₂ + а₃ х₃ + а₄ х₄

 yх₁ = а_о х₁ + а₁ х₁² + а₂ х₂ х₁ + а₃ х₃х₁ + а₄ х₄х₁

 yх₂ = а₀ х₂ + а₁ х₁х₂ + а₂ х₂² + а₃ х₃х₂ + а₄ х₄х₂

 yх₃ = а₀ х₃ + а₁ х₁х₃ + а₂ х₂х₃ + а₃ х₃² + а₄ х₄х₃

 yх₄ = а₀ х₄ + а₁ х₁х₄ + а₂ х₂х₄ + а₃ х₃х₄ + а₄ х₄²

При проведении качественного анализа необходимо понимать, что корреляция может быть обусловлена непосредственной зависимостью между x и y, общей зависимостью от третьей величины, неоднородностью материала или быть чисто формальной. Причинная зависимость существует, например, между временем работы и стоимостью производственной продукции, между весом станков и их стоимостью, между мощностью предприятия и себестоимостью его продукции.

Корреляция вследствие неоднозначности возникает из-за значительного разброса статистических данных и она полностью исключается проверкой нулевой гипотезы.

Чтобы избежать типичной ошибки - нахождения и расчета беспричинных формальных корреляций, необходимо провести качественный логический экономический анализ. И если причинной связи между факторами не существует, то бессмысленно проводить математическую обработку фактических данных.

При проведении корреляционного анализа надо учитывать также, что достоверное уравнение регрессии можно получить только при использовании однородного статистического материала. Выражением количественной однородности может служить коэффициент вариации. Величина коэффициента вариации, служащая границей между однородностью и неоднородностью статистической совокупности составляет 0,33. Величина коэффициента вариации  показывает, что совокупность данных по рассматриваемому признаку неоднородна. Поэтому необходимо расчленить исходную неоднородную совокупность на однородные части (группы). В данном выражении _x - величина среднеквадратического отклонения, - средняя арифметическая величина исследуемого признака.

После решения системы нормальных уравнений, получения коэффициентов регрессии и уравнения регрессии необходимо рассчитать показатели тесноты связи. Для многофакторной модели и при нелинейной зависимости теснота связи измеряется величиной индекса корреляции, рассчитываемого по формуле

,

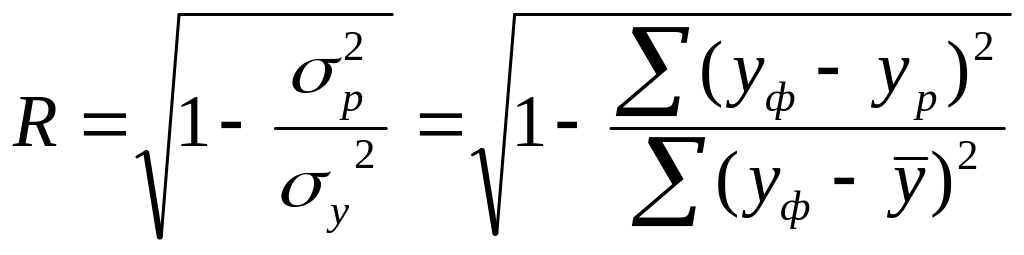где _р² =  (y_ф – y_р)²/n, _у² =  (y_ф -_y)²/n, y_р - значение изучаемого признака, рассчитанного по уравнению регрессии.

Для определения величины индекса корреляции нужно вычислить для каждого реального объекта значение y_р по найденному уравнению регрессии. Далее для каждого объекта определяется разность действительного значения y_ф и вычисленного по уравнению регрессии y_р. Сделав это по всем объектам, находят средний квадрат отклонений или остаточную дисперсию вычисленных значений от фактических. Далее определяется средний квадрат отклонения фактических значений признака y_ф от среднего по изучаемой совокупности того же признака, т.е. общая дисперсия. Полученные величины подставляются в формулу индекса корреляции.

При изучении парной линейной корреляционной зависимости между двумя признаками теснота связи определяется расчетом значения коэффициента корреляции по следующей формуле

где n - число изучаемых объектов в статистической совокупности.

Для качественной оценки тесноты связи может использоваться следующая шкала:

r < 0,3 - слабая связь;

0,3  < r < 0,7 - средняя связь;

0,7  <  r < 0,9 - высокая связь;

0,9  < r - весьма высокая связь.

И хотя при малой статистической совокупности можно получить высокую корреляционную связь между изучаемыми признаками, но тем не менее пользоваться полученным уравнением регрессии нельзя из-за его низкой надежности.

При проведении корреляционно-регрессионного анализа производят статистическую оценку значимости коэффициента корреляции и коэффициентов уравнения регрессии. Для этого определяют среднеквадратическую ошибку _r коэффициента корреляции (p – число факторных переменных):

Отношение величины коэффициента корреляции к его среднеквадратической ошибке дает величину t-критерия Стьюдента: t = r/_r. Принято считать, что если t > 2, то это свидетельствует о надежности полученного коэффициента корреляции. Вероятность такого утверждения составляет 0,95, и наоборот, если t < 2, это свидетельствует о недостаточной надежности исчисленного коэффициента.

Полученная величина коэффициента корреляции используется для оценки статистической значимости коэффициента уравнения регрессии (а_i). Для этого исчисляется его среднеквадратическая ошибка (_аi).

, ,

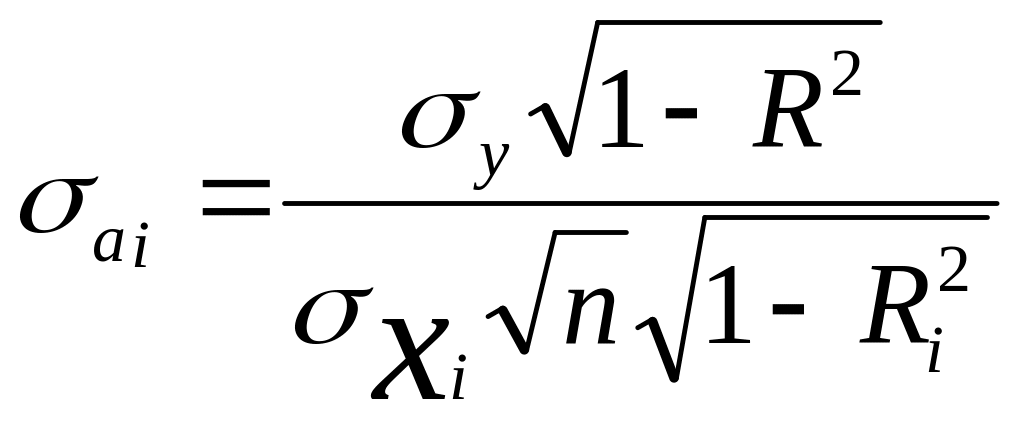где R_i² – коэффициент множественной корреляции x_i-го фактора с другими факторами (без результативного признака у), σ_xi – среднее квадратическое отклонение x_i-го факторного признака.

Коэффициент уравнения регрессии сопоставляется с его среднеквадратической ошибкой. В результате получается отношение t_ai = a_i / _аi. Если t_ai > 2, полученный коэффициент a_i следует считать значимым и соответствующий фактор x_i остается в уравнении множественной регрессии; если полученный коэффициент нельзя признать значимым (t_ai < 2), то соответствующий параметр исключается из уравнения множественной регрессии. По оставшемуся набору значимых факторов определяется окончательное уравнение множественной регрессии.

Влияние отдельных факторных признаков на результативный признак в едином масштабе в процентах можно определить по частным коэффициентам эластичности, которые характеризуют, на сколько процентов изменится уровень результативного признака y при изменении x_i-го факторного признака на 1 %.

Частный коэффициент эластичности определяется по формуле

Э_i = а_i  (x_i / y),

где Э_i - частный коэффициент эластичности; а_i - коэффициент уравнения множественной регрессии в натуральном масштабе при x_i-м факторном признаке;x_i - среднее значение x_i-го факторного признака;y - среднее значение результативного признака.

Показателем абсолютного отклонения оценок результативного признака является среднеквадратическое отклонение оценок результативного признака, рассчитанных по уравнению регрессии, от их фактических значений, которая определяется по формуле:

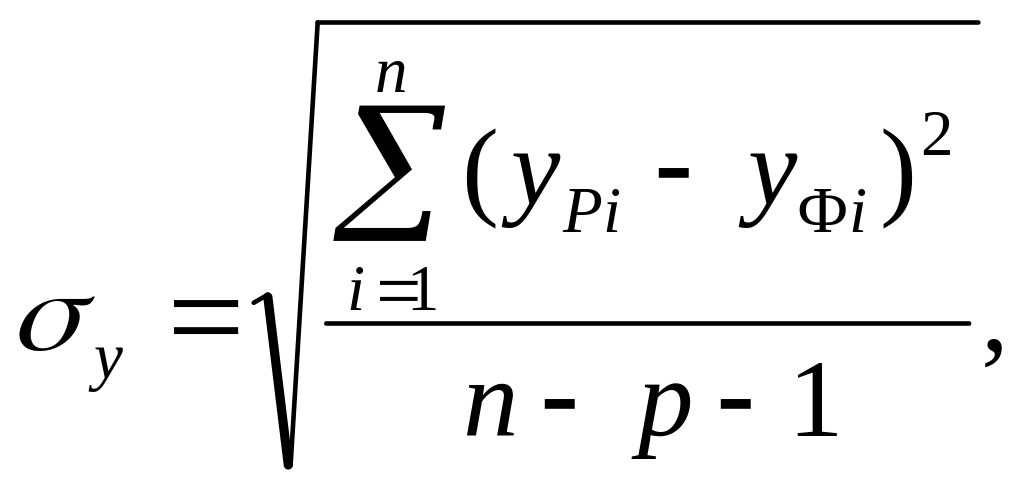
где n - число наблюдений в выборке; р - число факторных признаков модели.

Данная величина используется для определения коэффициента вариации

,

где - среднее значение результативного признака.

Определить предполагаемую величину себестоимости нового изделия на стадии технического задания и технического предложения средствами укрупненного расчета.

Исходные параметры для определения себестоимости электродвигателя: мощность 630 кВт; КПД - 93,7 %; масса 6550 кг; число оборотов в минуту 375.

Статистические данные по продукции аналогичного типа:

Номер изделия	Мощность, кВт	КПД, %	Масса, кг	Число оборотов в минуту	Себестоимость, ден.ед.
1	1000	95,0	4800	1000	9500
2	1250	95,2	5450	1100	10400
3	1600	95,4	7400	1000	11800
4	2000	95,7	8000	1000	13300
5	8000	94,7	4700	750	9500
6	1000	95,0	5250	750	10400
7	1250	95,2	7250	750	11500
8	1600	95,5	7500	750	13100
9	630	94,5	4600	750	9300
10	800	94,6	5160	600	10300
11	1000	94,6	6700	600	11300
12	1250	94,6	7650	600	12600
13	1600	95,2	8900	600	14300
14	500	93,3	5890	375	10000

Примечание: предполагается, что между факторами имеется линейная корреляционная зависимость.

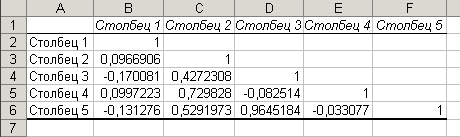
Рис. 12. Парные коэффициенты корреляции

На рис. 12 показан результат расчёт линейных парных коэффициентов корреляции, а на рис. 13 – результаты проведения корреляционно-регрессионного анализа с помощью инструментов Корреляция и Регрессия из пакета Анализ данных электронной таблицы Excel.

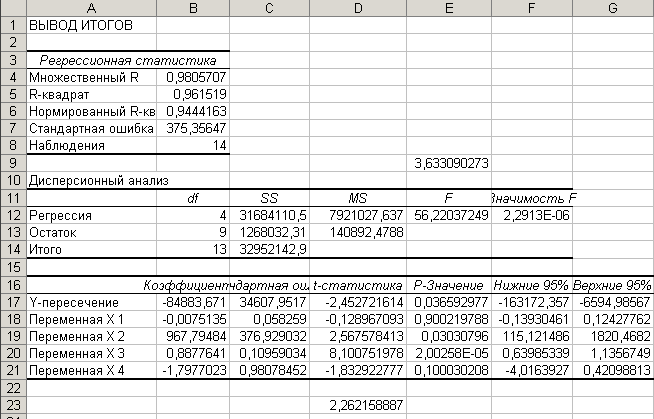
Рис. 13. Результаты корреляционно-регрессионного анализа

В примере предполагается, что на уровень себестоимости продукции (результативный признак - Y) оказывает влияние ряд факторных признаков, таких, например, как мощность (X₁), КПД (X₂), масса (X₃) и число оборотов в минуту (Х₄).

Исходя из экономической сущности влияния факторных признаков на результативный, выбираем линейное уравнение регрессии

у = а₀ + а₁х₁ + а₂х₂ + а₃х₃ + а₄х₄.

Данная задача решается на ЭВМ с помощью программы корреляционно-регрессионный анализ. В качестве исходных данных вводятся соответствующие значения факторных признаков и результативного признака по всем исследуемым источникам информации (предприятиям). В результате решения на ЭВМ получаем значения коэффициентов парной корреляции, параметров уравнения регрессии и коэффициента множественной корреляции:

а₀ = -15403,631; а₁ = 3,1616; а₂ = 250,454; а₃ = 0,3098;

а₄ = -3,729; R = 0,993.

Применяя возможность параметрического расчета на ЭВМ, вводим известные значения параметров для вновь проектируемого изделия, себестоимость которого еще не определена и получаем прогнозное значение Sпр = 10686,4 денежных единицы. При необходимости дальнейшего анализа полученных данных рассчитывается дисперсия, коэффициент вариации, коэффициент эластичности.

Применение корреляционно-регрессионного анализа для прогнозирования динамики экономических явлений. Прогнозирование осуществляется на основе собранных числовых статистических данных, характеризующих изменение экономических процессов или явлений. Такие числовые данные в виде конкретных показателей, изменяющихся во времени, образуют ряд динамики или временной (динамический, хронологический) ряд. Для дальнейшего прогнозирования необходимо подобрать аналитическую функцию (прямую или кривую), наиболее точно характеризующую закономерность развития данного явления или процесса во времени. Найденная функция позволяет получить выровненные значения уровней ряда динамики (его теоретические оценки), т.е. те уровни, которые наблюдались бы, если бы динамика явления или процесса полностью совпадала с выбранной кривой (линией регрессии).

Основными методами преобразования наблюдаемых статистических значений исследуемых показателей к аналитическому виду являются интерполяция, аппроксимация и экстраполяция (рис. 14).

Известно, что через любые n + 1 точки можно всегда провести кривую, описываемую полиномом n-й степени, так, чтобы она прошла через каждую из заданных точек а₁, а₂, ..., а_n. Эта кривая называется интерполирующей, а процесс её нахождения - интерполяцией. Однако в практике моделирования производственно-экономических объектов применяются интерполяционные полиномы невысоких степеней (ввиду проблемы интерпретации сложных зависимостей), в первую очередь для вычисления промежуточных значений, отсутствующих в таблице. Простейшим случаем является линейная интерполяция, т.е. интерполяция функции f(х) линейной функцией F(х).

Рис. 14. Уравнение и линия тренда

Для получения более “гладкого” вида интерполирующей кривой при линейной интерполяции применяются формулы Ньютона. При параболической и квадратичной интерполяции полином второй степени используется формула Лагранжа. Программы интерполяции входят в стандартное математическое обеспечение ЭВМ.

Во многих случаях для функции, заданной таблично или графически, бывает целесообразно подобрать аналитическое выражение, приближенно её отражающее. Такой процесс называется приближенной интерполяцией или аппроксимацией. Для приближения заданной функции f(х) выбирают аппроксимирующую функцию F(х) из классов математических функций, в наибольшей степени соответствующих специфике протекания исследуемого процесса.

Наибольшее распространение в практике экономических исследований получили следующие функции:

линейная ;

степенная ;

экспоненциальная ;

показательная .

Процесс подбора эмпирической формулы для установленной из опыта функциональной зависимости является итерационным и распадается на две части: выбирается вид формулы; определяются числовые значения параметров, для которых приближение к данной функции оказывается наилучшим.

Для решения первой задачи по экспериментальным данным строятся графики, по которым и выбирается вид аппроксимирующей зависимости. Для решения второй задачи существует ряд методов приближения эмпирической кривой к экспериментальной, например, приближение по методу наименьших квадратов.

Особую роль вопросы экономного представления табличной информации в аналитическом виде играют при обработке статистической информации, в связи с чем в рамках математической статистики получили развитие разделы однофакторного и многофакторного регрессионного анализа. Программы обработки статистических данных методами регрессионного анализа также представлены в стандартном математическом обеспечении ЭВМ.

Экстраполяция - это продолжение интерполяции и аппроксимации за пределы диапазона статистических данных. Если исследуемый фактор - время, то это прогнозирование в будущее. Предположение, что действие различных факторов, обусловливающих явление в прошлом, остается неизменным в течение будущего периода или будет меняться в соответствии с расчетной кривой, позволяет прогнозировать это явление в будущем.

Прогнозная экстраполяция строится на основе математического анализа исходного ряда с учетом логики и существа развития объекта, его физики и абсолютных пределов.

Этапы прогнозной экстраполяции: предварительная обработка исходного ряда; выбор типа аппроксимирующей функции; расчет параметров аппроксимирующей функции; экстраполяционная оценка точности и достоверности результатов.

Для определения параметров уравнения регрессии используется метод наименьших квадратов, который требует, чтобы сумма квадратов отклонений значений, лежащих на линии регрессии (теоретических оценок уровней), от фактических значений уровней была минимальной, т.е. чтобы соблюдалось условие  (y_р – y_ф)²  min, где y_ф - фактическое значение уровня динамики, y_р - теоретическая (расчетная) оценка уровня.

Аналитическим выражением прямолинейного тренда является функция

y_t = b₀ + b₁ t,

где b₀ и b₁ - параметры уравнения регрессии; t - очередной номер уровня ряда с начала отсчета (номер временного периода).

Для определения параметров тренда необходимо решить систему нормальных уравнений

 y_t = b₀  n + b₁ t,

 y_t  t = b₀ t + b₁ t²,

где n - количество значений ряда динамики.

Произведя преобразования, получим:

b₀ = ( y_t – b₁ t )/n,

b₁ = (n y_t t -  t  y_t)/(nt² - (t)²).

Коэффициент корреляции определяется по формуле:

где y_t - фактическое значение показателя динамического ряда за t-й период (момент); y_t - среднее значение показателей динамического ряда; t - условный номер t-го периода;t - средняя величина условных номеров периодов; n - количество наблюдений в ряду.

Интервал, в котором с определенной вероятностью можно ожидать появление фактического значения прогнозируемой величины, называется доверительным интервалом. Величина доверительного интервала зависит от среднеквадратической ошибки оценки прогнозируемого показателя (_yt), от времени учреждения прогноза (Т) и от количества периодов наблюдения во временном ряду (n):

где y_фt - фактическое значение показателя динамического ряда за t-й интервал (момент) времени; y_рt - расчетная оценка показателя динамического ряда по уравнению регрессии; n - количество моментов во временном ряду; k - число параметров в уравнении регрессии.

Тогда для прямолинейного тренда доверительный интервал прогноза можно определить по формуле:

где Y_n+T - прогноз на n+Т-й период времени; t_;n-2 - значение критерия Стьюдента при уровне значимости  и n-2 степенях свободы.

Пусть требуется определить прогнозную оценку некоторого показателя на три предстоящих месяца, имеется статистика изменения этого показателя за девять предшествующих месяцев:

1	2	3	4	5	6	7	8	9
59,319	68,921	74,088	91,125	97,336	103,823	125,0	140,608	148,877

После решения задачи на ЭВМ получим параметры уравнения регрессии, коэффициент корреляции и прогнозную оценку рассматриваемого показателя на соответствующий момент времени:

b₀ = 43,69; b₁ = 11,46; r = 0,98;

подставив в уравнение тренда значения t = 10; 11; 12, получим: Y₁₀ = 158,33; Y₁₁ = 169,79; Y₁₂ = 181,256.

Для каждого полученного прогнозного значения необходимо рассчитать доверительный интервал.