
Теоретические основы химической технологии (ответы на билеты)
.pdf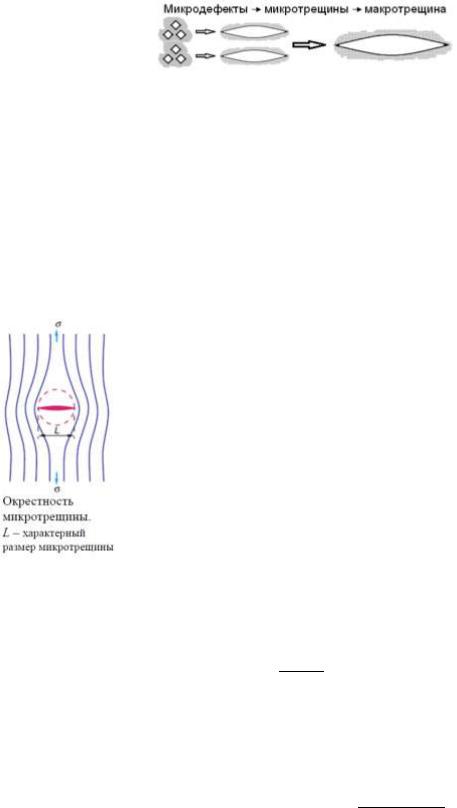
26. Энергетическая теория разрушения твердых тел А.Гриффитса, формула Гриффитса. Уточнение формулы Гриффитса с учетом вязкой реакции материала на нагрузку. Кинетическая теория разрушения твердых тел С.Н.Журкова. Физическое подобие формул С.Н.Журкова и Я.И.Френкеля.
В объеме однородного тела работа внешней нагрузки равномерно распределяется в виде деформационной (упругой) составляющей внутренней энергии тела. Но области вокруг микродефектов разгружены, и упругая энергия, которая в отсутствии дефектов была бы распределена в этих областях, концентрируется на «углах» микродефектов. С ростом нагрузки повышается вероятность слияния соседних микродефектов в микротрещину. При этом область вокруг микротрешины разгружается. В отличие от микродефекта микротрешина имеет поверхность, поэтому высвобожденная упругая энергия частично аккумулируется в виде поверхностной энергии. C дальнейшим увеличением нагрузки устойчивость микротрещин снижается. После достижения критической для данного материала нагрузки начнется слияние соседних микротрещин в макротрещины, а затем во фрагменты тела. Тем самым, реализуется механизм каскадного преобразования работы внешних сил в поверхностную энергию макротрещин и фрагментов тела.
Гриффитс, объединив термодинамику и механику, предложил термомеханическую, или энергетическую модель разрушения твердого тела. Рассмотрим её на примере плоского образца твёрдого материала.
Согласно теории Гриффитса, вся высвобождаемая при деформации энергия переходит в поверхностную энергию образующейся трещины:
= 2 , |
− коэффициент поверхностного натяжения |
|||||
|
|
|
|
|
|
|
|
При увеличении размера трещины за счёт деформационной силы |
|||||
на изменение поверхностной энергии составит: |
|
|||||
|
||||||
|
= = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина |
|
выражает |
интенсивность |
высвобождения |
|
|
|
|||||
|
|
|
|
|
|
|
деформационной энергии с ростом трещины. Значение этой производной
взятой с обратным знаком носит название трещинодвижущей силы = − |
|
|||||
|
||||||
|
|
|
|
|
||
Трещинодвижущая сила связана с характеристиками напряжённого |
||||||
состояния: модулем Юнга E и коэффициентом Пуассона уравнением: |
|
|||||
|
|
|
(1 + )(̃ + 1) |
|
||
|
|
= − 2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
||
|
|
|
||||
– коэффициент интенсивности напряжений
̃ = 3 − 4 − для плоской деформации
Подставляя выражение для трещинодвижущей силы в уравнение энергии поверхностного натяжения и преобразую полученное выражение, получим критический коэффициент интенсивности напряжений:
(1 + )(̃ + 1) 2 |
|
|
2 |
|
= 2 |
= √ |
|
|
|
||
4 |
|
|
1 − 2 |
|
|
Рост трещины начинается, когда коэффициент интенсивности напряжений превосходит критическую величину. В противном случае трещина может сохраняться внутри тела сколь угодно долго. Для наиболее простого случая равномерно-нагруженной бесконечной тонкой пластины
внутри которой расположена трещина длины , коэффициент интенсивности напряжений равен:
|
|
|
|
|
|
|
|
2 |
|
= √ , |
когда = , |
= |
|
|
= √ |
|
|||
|
|
|
|||||||
|
|
|
|
√ |
|
(1 − 2) |
|||
|
|
|
|
|
|
|
|||
Полученное уравнение носит название Формула Гриффитса
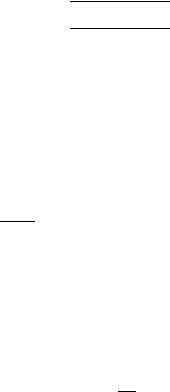
После достижения критической для данного напряжения длины трещина неудержимо растет. В реальной жизни это наблюдают только в случае хрупких материалов, таких как стекло, керамика. Дж. Ирвин, предложил помимо трансформации упругой энергии в поверхностную энергию учитывать диссипацию упругой энергии в процессе пластической деформации. Пластическая деформация повышает сопротивляемость тела хрупкому разрушению. С введением поправки Ирвина теория Гриффитса может быть распространена практически на все материалы. Введённый безразмерный фактор М учитывает пластическое деформирование материала у концов трешины:
2= √ (1 − 2)
В реальности любая макротрещина начинает свой рост ещё с докритических размеров Согласно теории С.Н.Журкова, причиной этого являются тепловые возмущения вызывающие флуктуации колебательной энергии «элементарных» частиц, составляющих материал. Эта флуктуация может достигать критических значений, достаточных для разрыва химических связей между частицами. Из экспериментов С.Н.Журкова следует, что чем больше приложенная к телу нагрузка при заданной температуре и чем больше температура при заданной нагрузке, тем меньшее время требуется для возникновения критических микротрещин, инициирующих разрушение тела.
Аппроксимация этих результатов представлена в виде логарифмической зависимости среднего времени ожидания разрушения от температуры и приложенной нагрузки :
( )
= + 0,0 − энергетический барьер разрыва межатомных связей (в пределах 10% совпадает с энергией
разрыва межатомных связей )
0 − постоянная порядка периода тепловых колебаний атомов 10-12 – 10-13с
− эмпирический коэффициент
Втеории конденсированного состояния известна формула академика Я.И.Френкелем. Эта формула позволяет оценить среднее время ожидания флуктуации энергии величины на
межатомной связи в твёрдом теле:
= 0
. Формальное подобие формул С.Н. Журкова и Я.И.Френкеля на самом деле имеет глубокий физический смысл. Действительно, элементарный акт разрушения начинается, когда флуктуация
энергии достигает величины , или точнее 0 − , т.е. более низкой величины вследствие
действия приложенного напряжения. Происходит разрыв межатомных связей, а накопление этих разрывов ведет к образованию микротрещин.

27. Композиционные материалы, классификация. Эффективный модуль Юнга композиционного материала на примере задачи о растяжении-сжатии цилиндра, армированного волокнами, расположенными перпендикулярно и параллельно образующей. Критерии качества композиционных материалов.
Композиционными называют материалы, состоящие из нескольких фаз (компонентов), свойства которых существенно различаются. Первый компонент – непрерывная фаза или матрица, может иметь керамическую, металлическую или полимерную природу. Второй компонент – армирующая фаза, или наполнитель, состоит из частиц разной природы и формы.
Взависимости от формы частиц наполнителя композиционные материалы подразделяют на:
1)Дисперсионно наполненные, или гранулированные, если характерный размер матрицы L и характерный размер l гранул наполнителя, связаны неравенством l << L;
2)Волокнистые, если включениями являются длинные цилиндры (волокна);
3)Слоистые, если компоненты композита примыкают друг к другу параллельными слоями
Новые функциональные качества композиционного материала в сравнении с однородным материалом являются следствием перераспределения нагрузки между компонентами композиционного материала. Рассмотрим это на следующем примере:
Матрица имеет цилиндрическую форму с характерными размерами L и r. В матрице содержатся волокна (Площадь поперечного сечения 0) двух типов:
1)продольные волокна (параллельные оси цилиндра), поверхностная плотность точек пересечения волокон с верхним торцом цилиндра равна n м2
2)поперечные волокна (перпендикулярные оси цилиндра), поверхностная плотность точек пересечения волокон с боковой поверхностью цилиндра равна m, м2)
Модуль Юнга матрицы Е*, много меньше модуля Юнга волокон Е, что позволяет пренебречь изменением свободной энергии матрицы в сравнении с изменением свободной энергии деформированных волокон.
Найдём работу, совершаемую внешней нагрузкой при деформации образца:
Закон Гука для композиционного материала: =
∆
− эффективный модуль Юнга композиционного материала
Тогда, приложенная сила и совершаемая ей работа равны:
= 2 = |
|
∆ |
∙ 2, |
= ∆ = |
|
(∆ )2 |
∙ 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдём работу, затрачиваемую на растяжение продольного волокна. При растяжении |
|
|||||||||||||||||||
образца растягиваются только продольные волокна, поскольку поперечные волокна почти не |
|
|||||||||||||||||||
оказывают сопротивления растяжению. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Закон Гука для продольных волокон: = |
∆ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда, приложенная сила и совершаемая ей работа равны: |
|
|
|
|
|
|
||||||||||||||
= = |
∆ |
∙ , |
= 2 = |
∆ |
∙ 2 |
, |
= ∆ = |
(∆ )2 |
∙ 2 |
|
||||||||||
|
|
|
|
|
||||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Найдём работу затрачиваемую на растяжение поперечного волокна. При сжатии образца |
|||||||||||||||||||
растягиваются только поперечные волокна, поскольку продольные волокна почти не оказывают сопротивления сжатию.
Закон Гука для поперечных волокон: = 2∆2 Тогда, приложенная сила и совершаемая ей работа равны:
|
= |
= |
2∆ |
∙ , |
|
= |
1 |
|
∙ 2 = ∆ , |
|
= 2∆ = 2 (∆ )2 |
|
||||
2 |
|
|||||||||||||||
|
0 |
|
0 |
|
2 |
|
|
0 |
|
|
0 |
|||||
Из условия несжимаемости при малых деформациях найдём соотношение между ∆ и ∆ |
|
|||||||||||||||
2 = = = ( + ∆ )2( − ∆ ) |
|
∆ |
= |
∆ |
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
||||||||||||
Тогда получим окончательное выражение для работы поперечных волокон:
= |
(∆ )2 |
2 |
||||
|
|
|
||||
2 |
||||||
|
0 |
|
||||
Сравнивая полученные выражения для работы, а также учитывая, что вследствие больших различий в модуле Юнга матрицы и наполнителя, вся работа расходуется только на растяжение волокон получим выражения для эффективного модуля Юнга при сжатии и растяжении:
|
= , |
|
= |
|
|
||||
|
||||
|
0 |
|
0 |
2 |
|
|
|
|
Основное преимущество композиционных материалов связано с их малой в сравнении с металлами плотностью при достаточно высоких характеристиках прочности. Часто необходимо минимизировать массу конструкции при сохранении ее прочности, например, в аэрокосмической промышленности.
Формулировка критерия качества зависит от характера напряжений и деформаций, которым подвергается материал. Выделяют три типа деформаций, для которых сформулированы соответствующие критерии качества:
При растяжении |
При сжатии |
При изгибе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
3 |
|
|
−1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
||||||||||||
|
|
|
|
|
−1 |
|
m~ ( |
|
) |
|
m~ ( |
√ |
) |
|
|||||||||||||||
|
m~ ( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Чем |
больше |
|
значение |
Чем |
больше |
|
значение |
Чем |
больше |
|
значение |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
критерия |
, |
тем |
меньшую |
критерия |
, |
тем меньшую |
критерия |
√ |
, |
тем меньшую |
|||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
массу |
будет |
иметь канат |
массу |
будет |
|
иметь опора |
массу |
будет |
иметь |
панель |
|||||||||||||||||||
сохраняя те же механические |
сохраняя те же механические |
сохраняя те же механические |
|||||||||||||||||||||||||||
характеристики. |
|
|
характеристики. |
|
|
характеристики. |
|
|
|||||||||||||||||||||
Композиционные материалы в большинстве случаев превосходят металлы и пластики по приведённым критериям качества.

28. Основные причины деформации твердого тела. Понятие о тензоре деформации. Деформация малой окрестности однородного материала, матрица тензора деформации. Главные оси тензора деформации. Использование главных осей для вычисления относительного удлинения и относительного объемного расширения при малой деформации.
Если внешние силы и внешние моменты взаимно скомпенсированы, то реакция твердого тела на силовые воздействия проявляется в виде растяжения или сжатия, что на микроскопическом масштабе внутри тела является следствием изменения длины или частичного разрыва межатомных связей. Внешне эти изменения проявляются в форме относительных смещений малых частей тела – деформации. Помимо внешних силовых воздействий деформация тела может быть следствием обмена тепловыми потоками с внешней средой и химических и фазовых превращений внутри тела.
В Декартовой системе координат с центром в точке О положение точки А отмечается вектором . Изза деформации точка А из положения . смещается в точку А' с положением + ( ). ( ) –вектор деформации точки А. Совокупность векторов деформации всех точек тела представляет собой векторноеполе деформации данного тела.
Если до |
деформации |
две близкие точки и |
+ разделял |
вектор |
то после деформации |
смещенные точки будет разделять вектор ′ = + ,
где = ( + ) − ( ).
Множество векторов представляет малую окрестность точки А. Множество векторов ′ представляет деформированную окрестность точки А. Множество векторов представляет поле векторов деформации окрестности точки А.
Декартовы координаты вектора деформации = (1, 2, 3) выражается через вектор = (1, 2, 3) формулой:
= ∑
Иначе говоря вектор является результатом применения тензора ̂ с декартовыми координатами матрицы = к вектору , а именно = ̂ ° . Тогда деформацию
окресности точки А можно представить в виде (E – единичный тензор):
′ = ∑ , = 1,2,3 или ′ = ( + ̂)°
Тензор ̂ = ( ) можно представить в виде суммы двух тензоров:
|
̂ |
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Cимметричного = |
|
( |
|
|
+ |
|
|
|
) – тензор деформаций, определяет растяжение или |
||||
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
сжатие малой окрестности точки при деформации тела |
||||||||||||||
|
|
̂ |
|
1 |
|
|
− |
|
||||||
|
Антисимметричного |
= |
|
( |
|
|
|
) – тензор поворотов, определяет поворот малой |
||||||
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
окрестности точки деформируемого тела вокруг оси.
Доказательство: квадрат расстояния равен скалярному произведению вектора на самого себя. Тогда квадрат расстояния между точками недеформированной, деформированной окресности точки и разница между ними равны:
3
2 = = ∑ 2 , |
|
′2 |
= ( + ) ( + ) = + 2 + |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∆2 = ′2 − 2 |
|
= 2 + = ∑ 2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
= |
|
( |
|
+ |
|
|
+ |
|
|
|
) ≈ = |
|
( |
|
+ |
|
) |
|||
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Однако рассматривать деформации удобней пользуясь не общей для всех точек системой координат, а построив локальную систему координат для каждой точки, выбрав в качестве
единичных векторов осей координат собственные векторы локального тензора деформации ̂ ( ). Собственные векторы вещественных симметричных матриц ортогональны. Оси такой локальной системы координат называют главными осями. Из определения собственного вектора тензора следует, что в системе координат с главными осями матрица тензора деформации в рассматриваемой точке тела имеет диагональный вид, где по диагонали расположены собственные значения матрицы.
До преобразования координат |
После преобразования координат |
||||||||||
|
|
11 |
12 |
13 |
|
|
(1) |
0 |
0 |
|
|
( |
|
) = ( 21 |
22 |
23) |
( |
) = ( |
0 |
|
(2) |
0 |
) |
|
31 |
32 |
33 |
|
|
|
|
||||
|
|
|
|
0 |
0 |
(3) |
|
||||
Диагональные координаты матрицы тензора деформаций в главных осях часто называют главными значениями. Если соседние точки разделял вектор, параллельный собственному вектору, то после деформации этот вектор сжимается или растягивается, не меняя свое направление.
Вернёмся к рассмотрению расстояний между точками после деформации, для чего выразим
величину ′2 через главные значения тензора деформаций: |
|
|
|
|
|
|
|
||||
′2 = 2 + ∆ 2 = ∑( + 2 |
|
|
|
|
|
1 |
0 |
0 |
|
||
|
) |
|
( ) = (0 |
1 0) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
0 |
0 |
1 |
|
|
′2 = (1 + 2 (1)) 2 |
+ (1 + 2 (2)) 2 |
+ (1 + 2 (3)) 2 |
|
|
|
|
|
||||
, |
или |
| ′| = √1 + 2 ( )| | |
|||||||||
1 |
|
|
2 |
3 |
|
|
|
|
|
|
|
Деформацию тела удобно представить в виде относительного удлинения:
уд |
|
| ′ |
| − | | |
|
|
|
|
( ) 1 |
|
|
|
|
|
|
|
||||||
|
|
|
= √1 + 2 ( ) − 1 ≈ {√1 + 2 ( ) |
1 + ( )} ≈ ( ) |
||||||
|
= |
|
|
|||||||
| | |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Из полученного уравнения следует, что относительные удлинения вдоль направлений главных осей равны соответствующим главным значениям матрицы тензора деформаций.
Теперь рассмотрим изменение объёма области при деформации (расширение). До деформирования малый элемент объёма равен = 1 2 3. Тогда в системе главных осей
элемент объёма после деформации равен: |
|
|
|
||||
′ = ′ |
′ ′ |
= (1 + (1))(1 + (2))(1 + (3)) |
≈ + ( (1) + (2) + (3)) |
||||
1 |
2 |
3 |
1 |
2 |
3 |
|
|
Как и деформацию, расширение удобно представить в виде коэффициента относительного |
|||||||
расширения, который в системе главных осей равен: |
|
|
|
||||
расш = |
′ − |
= (1) + (2) + (3) |
|
|
|
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
Как видно из полученного выражения, коэффициент относительного расширения равен
сумме диагональных элементов матрицы или следу матрицы. Поскольку след матрицы инвариантен относительно преобразований системы координат, то и коэффициент относительного расширения является инвариантом преобразований системы.
29. Напряжения в статичном теле, тензор напряжений. Главные оси тензора напряжений. Дивергентная сила. Условие механического равновесия деформированного тела. Сопоставьте результаты экспериментов академика С.Н.Журкова с понятием о механическом равновесии тела под нагрузкой. Термодинамика деформации: работа сил внутреннего напряжения при малой деформации, свободная энергия и ее зависимость от деформации вблизи равновесия. Коэффициенты Ламе. Обобщенный закон Гука.
Напряжение – силы, возникающие в деформируемом теле, характеризующие сопротивление изменению расстояния между частицами в сплошной среде.
В твердом теле выделяется произвольный объем V, ограниченный замкнутой поверхностью Σ, и рассматриваются все силы, действующие на тело внутри выделенного объема. В соответствии с третьим законом Ньютона внутренние силы взаимно компенсируют друг друга. Внешние силы, действующие на выделенный объем тела, подразделяют на объемные (дальнодействующие, массовые), и поверхностные (близкодействующие). Массовые силы обусловлены взаимодействием частей тела с внешними телами и силовыми полями. К ним относится, например, сила тяжести.
Природа поверхностных сил иная. В результате деформации под действием внешней нагрузки части тела сдвигаются друг относительно друга, и, как следствие, появляются силы, стремящиеся вернуть их в исходное положение механического равновесия. По своей природе это межмолекулярные силы, действующие только вблизи поверхности Σ.
Таким образом, если пренебречь полем тяжести и электромагнитным полем, то на выделенный объем твердого тела оказывают воздействие только поверхностные силы.
|
|
|
|
|
|
|
|
|
Поверхностную силу ( ), в каждой точке поверхности Σ представляют результатом действия |
||||||||
оператора , называемого тензором напряжений, на нормаль ( ) к элементу поверхности: |
||||||||
|
|
|
|
Н |
11 |
12 |
13 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
|
|
( ) [ ] = ( |
||||||
( ) = ° ( ), |
|
21 |
22 |
23) |
||||
|
|
|
м2 |
31 |
32 |
33 |
||
|
|
|
|
|||||
|
|
|
|
|
|
|||
Столбцы матрицы |
тензора напряжений являются |
координатами сил, действующих на |
||||||
единичные площадки, параллельные координатным плоскостям Декартовой системы координат. Для упрощения матрицы тензора напряжений перейдём в локальную систему координат для каждой точки поверхности. Оси новой системы координат направлены вдоль собственных векторов
локального тензора ( ). В построенной системе координат тангенциальные составляющие |
||
действующих на поверхность сил равны 0, а матрица приводится к виду: |
||
11 |
0 |
0 |
( ) = ( 0 |
|
0 ) |
|
22 |
|
0 |
0 |
33 |
Результирующая сила, действующая на весь объём тела, ограниченного поверхностью Σ равна сумме сил действующих на каждый элемент поверхности ds:
|
Остроградский−Гаусс |
|
|
||
∫ () = ∫ ° () |
() = () |
|
Применив теорему Остроградского-Гаусса и перейдя к пределу → 0 определим силу , действующую на единичный объём с центром в точке . Эту силу называют дивергентной или объёмной силой. Объёмная сила характеризует локальное внутреннее напряжение в точке . Чтобы наглядно сформулировать условие механического равновесия деформированного тела, запишем дивергентную силу в координатном виде:
|
|
|
|
|
или = ∑ |
|
, при равновесии = 0 |
|
|||
( ) = ( ) |
|
||
|
|
|
|
|
|
|
|
|
|
|
В равновесии в каждом объеме тела внутренние напряжения должны взаимно компенсироваться. Неразрушающая деформация упругого тела состоит в переходе от начального равновесного недеформированного состояния к конечному равновесному деформированному состоянию. При этом деформация происходит из-за действия дивергентных сил.
Сопоставьте результаты экспериментов академика С.Н.Журкова с понятием о механическом равновесии тела под нагрузкой
Вспомним суть рассматриваемых экспериментов. Стандартные образцы материалов подвергали статической нагрузке. В результате в зависимости от величины нагрузки (меньше предела прочности) и температуры образец разрушался. Причём, чем выше нагрузка и температура, тем разрушение происходило быстрее. Журков предположил, что это происходит вследствие флуктуаций тепловых движений атомов, которые могут привести к разрыву межатомной связи.
Поскольку нагрузка на образцы статическая, внешние силы компенсированы и любое изменение внутри образцов вызвано дивергентными силами. На внутренних дефектах структуры возникают концентрации напряжения. Чтобы перевести образец в равновесное состояние, дивергентные вызывают деформации в образце, которые могут привести к разрыву межатомных связей. (Но вообще говоря странно сопоставлять теорию неразрушающей деформации и эксперименты результатом которых являлось разрушение материала)
Работа дивергентных сил
|
|
|
|
|
= = ∫ ∙ = ∫ (∑ |
|
) |
||
|
||||
|
|
, |
|
|
|
|
|||
После интегрирования полученного выражения по частям и нескольких преобразований получим:
= − ∫ (∑ |
|
|
) или |
= − ∑ |
|
|
|
|
|
|
|
|
|
|
|||
|
, |
|
|
|
, |
|
|
|
|
|
Термодинамика деформации |
|
|
|
|||
Запишем основное термодинамическое тождество для обратимо деформируемых тел с учётом работы сил внутреннего напряжения :
= − = + ∑
,
Определим свободную энергию тела следующим выражением:
Ф = − |
или Ф = − + ∑ |
|
|
, где |
|
= |
Ф |
| |
|
|
|
||||||
|
|
|
|
|
|
|
||
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изменение свободной энергии тела при растяжении или сжатии всегда положительно, т.к. в обоих случаях внешние силы затрачивают работу на смещение атомов из положения равновесия. Следовательно выражение для свободной энергии Ф не линейно и должно являться чётной функцией. Исходя из этого свободную энергию представляют в виде:
2
3
Ф = Ф0 + 2 (∑ ) + ∑ 2
=1 ≠
Параметры , называются коэффициентами Ламэ и определяют механические свойства изотропных твёрдых тел. Найдём связь между коэффициентами Ламэ и модулем Юнга и коэффициентом Пуассона. Для этого получим обобщённый закон Гука в тензорной форме:
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
= (∑ ) + 2 ( |
|
− |
(∑ ) ) |
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
=1 |
|
||||
|
Ф |
|
=+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
|
|
|
или |
|
|
|
|
|
|
|||||||
= |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
= |
(∑ ) + |
( − |
(∑ ) ) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
9 |
|
|
2 |
|
|
3 |
|
|
||||
|
|
|
|
|
{ |
|
|
=1 |
|
|
|
=1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Связь между коэффициентами описывается следующими выражениями:
= |
9 |
= |
1 3 − 2 |
||
|
|
|
|
||
3 + |
2 3 + |
||||
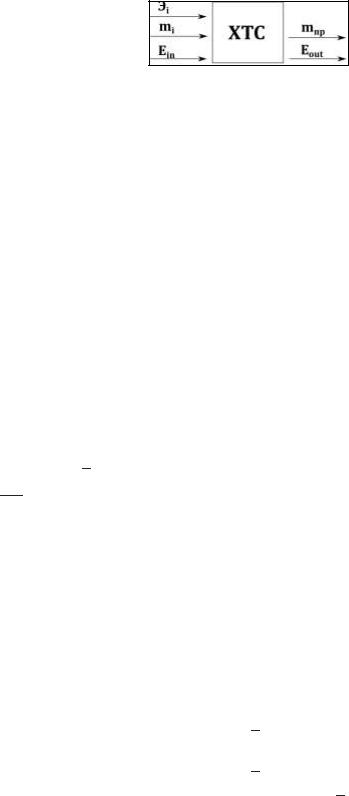
1. Показатели эффективности действующих производств. Технологические и экономические показатели. Ресурсы предприятия, формирование затрат на производство, калькуляция себестоимости продукции. Структура цены товарной продукции, модели ценообразования. Анализ порога безубыточности.
Для оценки эффективности действующих производств, рассмотрим следующий упрощённый пример:
Пусть имеется химико-технологическая система (ХТС), на входе подается mi исходного сырья, Эi энергии и Еin эксергии. На выходе получаем mпр готового продукта и Eout эксергии. Тогда:
1) Критерий эффективности использования сырья
определяется законом сохранения массы и стехиометрией реакции. Используют следующие показатели: расходные коэффициент компонентов и исходного
сырья и выход продукта: |
= |
|
( |
т |
или |
кг |
) |
= |
теор |
∙ % |
|||
|
|
|
|
|
|
||||||||
пр |
т |
т |
практ |
||||||||||
|
|
|
|
|
|
|
|||||||
2) Критерий эффективности использования энергоресурсов. Используют следующие показатели: расходный коэффициент энергии и энергетический КПД процесса:
э = |
Э |
(кВт час/т) |
КПД = |
э теор |
|
∙ % |
||||
|
э практ |
|||||||||
|
пр |
|
|
|
|
|
||||
3) Критерий ТМД совершенства ХТС (эксергетический анализ). |
Используют следующие |
|||||||||
показатели: удельные потери эксергии и эксергетический КПД процесса: |
|
|||||||||
|
Е = |
Е − Е |
|
= |
∑ |
∙ % |
||||
|
пр |
∑ |
||||||||
|
|
|
|
|
|
|
||||
4) Критерий компактности технологической схемы – определяется законами макрокинетики, выражающими интенсивность протекающего процесса. Используют следующие показатели: производительность оборудования (П), максимальная производительность (мощность оборудования), интенсивность аппарата (U) – отношение производительности реактора к размеру аппарата:
П = |
пр |
(т⁄час) |
= |
П |
( т⁄м ∙ час) |
|
|
|
|
||||
5)Критерий экологической безопасности технологической системы.
6)Критерии экономической эффективности. Пример: стоимость исходных ресурсов = З рублей. Стоимость продукции = R рублей. Самый простой критерий – это прибыль П = R – З.
Относительная величина – индекс доходности: ИД = З (руб⁄руб)
Рентабельность производства: РП = −З З (руб⁄руб)
Прибыль, индекс доходности, рентабельность производства – это интегральные и слишком общие характеристики, которые не дают возможности провести детальный анализ экономики производства.
Стоимость продукции определяется произведением цены единицы продукции на ее количество = Ц ∙ . Затраты складываются из следующих ресурсных составляющих: фонд заработной платы (ФЗП, трудовые ресурсы), основные производственные фонды (ОПФ,
используемые в ходе производства оборудования, здания, сооружения со сроком службы больше года), стоимость Ф рублей, которые нужно учитывать в амортизационных отчислениях А = На ∙ Ф , оборотные фонды (ОС, исходное сырье, вспомогательные материалы, которые расходуются в рамках 1-го производственного цикла), информация (нематериальный актив, ноу-хау и т.д.) и другие накладные расходы ∆:
З = ФЗП + А + ОС + ∆
Показатели для ОПФ:
Фондоотдача – отношение выручки к среднегодовой стоимости фондов: ФО = Ф Фондоемкость продукции – показывает величину стоимости основных производственных
фондов, приходящихся на единицу продукции, выпущенную предприятием: ФЕ = Ф Рентабельность фондов – отношение прибыли к среднегодовой стоимости фондов: РФ = ФП

Показатели для ОС:
Коэффициент оборачиваемости оборотных средств = выручка от продаж/оборотные активы. Оборотные активы берутся как среднее значение на начало и конец отсчетного периода. Коэффициент показывает сколько раз за выбранный период (год, месяц, квартал) оборачиваются
оборотные средства: К = ОС
Пусть за год предприятие реализовало продукцию на 24 млн. руб., а стоимость оборотных фондов составила 6 млн. руб. Тогда число оборотов в год или коэффициент оборачиваемости равен
4.
Длительность одного оборота оборотных средств: в примере выше длительность одного оборота составит: 12/4= 3 месяца.
Как частный случай фондоемкости вводят материалоемкость – отношение стоимости затраченных материалов, сырья к стоимости продукции, и энергоемкость – отношение стоимости энергии к стоимости продукции.
Показатели для трудовых ресурсов:
Производительность труда – отношение финансовых результатов производства к среднесписочной численности обслуживаемого персонала: ПТ = Ч(сп)
Также производительность труда можно представить, как отношение количества выпущенной продукции в единицу времени. Обратная величина называется трудоемкостью –
затраты труда в человекочасах на единицу продукции: |
|
|
|
|||||
|
ПТ = |
|
= |
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|||||
|
Себестоимость продукции – затраты на производство и реализацию единицы продукции. |
|||||||
|
Пример калькуляции себестоимости 1 тонны аммиака: |
|
||||||
№ |
Наименование прибавки к стоимости |
|
|
Стоимость, руб. |
Отношение к |
|||
|
|
стоимости товара, % |
||||||
|
|
|
|
|
|
|
|
|
1 |
Сырье и материалы |
|
|
175,93 |
19,7 |
|||
2 |
Энергия для технологических целей |
|
|
315,94 |
35,4 |
|||
3 |
Заработная плата рабочих |
|
|
24,78 |
2,8 |
|||
4 |
Износ катализаторов |
|
|
1,59 |
0,2 |
|||
5 |
Общепроизводственные расходы (амортизация) |
|
166,93 |
18,7 |
||||
6 |
Производственная (цеховая) себестоимость |
|
|
684,87 |
76,9 |
|||
7 |
Прочие производственные расходы |
|
|
210,06 |
23,6 |
|||
8 |
Полная себестоимость |
|
|
891,11 |
100 |
|||
9 |
Прибыль (рентабельность) |
|
|
89,11 |
10 |
|||
10 |
НДС (налог на добавленную стоимость) |
|
|
196,04 |
22 |
|||
11 |
Отпускная цена |
|
|
1176,26 |
132 |
|||
Такой подход формирования цены – затратный подход. Существует и другой подход формирования цены – рыночный, где покупатели определяют цену, исходя из предложения товара на рынке.
Точка безубыточности (порог рентабельности) – это такая выручка (либо количество продукции), которая обеспечивает полное покрытие всех переменных и условно-постоянных затрат при нулевой прибыли. Определить точку безубыточности можно из графика:
Анализ порога безубыточности позволяет оценить, сколько товаров по той или иной цене необходимо продать, чтобы «погасить» затраты при производстве этого товара.
