2.5.4. Предикаты на конечных областях. Логика одноместных предикатов

Рассмотрим некоторые свойства формул логики предикатов, относящиеся к фиксированному множеству.

Пусть в начале область m конечна, а₁, а₂, …,а_n – ее элементы. Тогда оказывается, что на m каждая формула равносильна формуле, не содержащей кванторов.

Этот факт следует из двух непосредственно проверяемых равносильностей:

VxA(x) = A(a₁)^...^A(a_n) и xA(x) = A(a₁)v...vA(a_n).

Пример 1. Доказать абсолютные равносильности:

Vx(A(x)^B(x)) = (VxA(x))^(yB(y));

x(A(x)vB(x)) = xA(x)v yB(y).

Проверяется по определению.

Пример 2. Проверить на противоречивость множество дизъюнктов .

Для доказательства противоречивости запишем дизъюнкты в таблицу. Результат каждого следующего шага также будем записывать в таблицу. Литеры, использующиеся на данном шаге будем подчеркивать.

Номер шага		Q	R
1		Q	R
2		Q	R
3		Q	R
4						0

На шаге 4 получаем 0. Это – резолютивный вывод из данного множества дизъюнктов. Следовательно, множество невыполнимо.

Пример: Показать, что формула равносильна 1 на любой области m (точнее на ), состоящей из одного элемента, но не абсолютно равносильна 1.

Эта формула не будет равносильна 1 уже на области из двух элементов. Пусть m состоит из элементов a и b и

А(а) = 0; А(b) = 1.

Примеры предикатов

Для того, чтобы привыкнуть к языку логики предикатов, рассмотрим несколько примеров.

1. Ввести одноместные предикаты на соответствующих областях и записать при их помощи следующие высказывания в виде формул логики предикатов:

а) всякое натуральное число, делящееся на 12, делится на 2, 4 и 6.

Введем на натуральном ряде предикаты:

А(х) – делится на 12 (т.е. А(х) = 1 тогда и только тогда, когда х делится на 12);

В(х) – делится на 2;

С(х) – делится на 4;

D(х) – делится на 6.

Тогда .

2.6. Операции над предикатами и кванторами

Выше нами установлено, что

1. Предикат — это функциональное высказывание, а высказывание — предикат­ная константа. Логика предикатов — это расширение логики высказываний за счет использования предикатов в роли логических функций. Эти функции несколько отличаются от функций, которые мы использовали в логике Буля. Булева функция однородна, т.е. для нее область значений функции и область изменений аргументов по типу одна и та же — логическая (либо истина, либо ложь). Для предикатов же область значений функции — логическая, а область изменений аргу­ментов — предметная. Таким образом, эта функция — неоднородна. Приведем примеры предикатных функций. Пусть имеется ряд простых высказываний:

= «Иван читает Достоевского»,

= «Петр читает Достоевского»,

= «Степан читает Достоевского».

Вместо высказываний мы могли бы ввести одноместный предикат P(x), для которого переменная х принимала бы значения из предметной области—

а сама предикатная функция передавалась бы словами:

= « x читает Достоевского».

Теперь изменим сходный ряд высказываний на другой:

= «Иван читает Достоевского»,

= «Петр читает Толстого»,

= «Степан читает Чехова».

Здесь можно было бы ввести уже двухместный предикат

с дополнительной предметной областью —

Введем трехместный предикат , который означает, что « х есть сумма y и z ». Допустим, в процессе вычислений переменная х приняла конкретное значение, равное 5. Тогда трехместный предикат превратится в двухместный:

При x = 5 и у = 3 получим одноместный предикат:

Наконец, если добавить условие , то исходный предикат становится нулъместным предикатом (константой или высказыванием), который в данном случае принимает истинное значение:

Но могло случиться, что тогда имели бы ложное высказывание:

Таким образом, при замещении переменной предметной постоянной происходит превращение

n-местного предиката -местный предикат— Приписав конкретные значения всем аргументам предикатной функции - , мы тем самым получаем предикатную константу, к которой применимы все законы логики высказываний.

2. Функциональная природа предиката влечет за собой введение еще одного понятия — квантора. Роль его выясним на следующих двух примерах:

1. «Все люди смертны. Сократ человек. Следовательно, Сократ смертен.»

2. «Некоторые люди гениальны. Сократ человек. Следовательно, Сократ гениален.»

Во втором примере хорошо чувствуется ложность заключения, поскольку интуитивно мы понимаем, что Сократ мог и не попасть в число гениальных людей.

Итак, ключевыми словами в наших примерах являются «все» и «некоторые». Когда какое-нибудь правило распространяется на всех индивидуумов, оно, естественно, распространяется и на Сократа. Когда же правило касается только некоторых, оно может оказаться в отношении Сократа как раз и неверным.

Термин «все х» обозначается в логике предикатов и называется квантором общности (символ есть перевер-нутая буква А, которая является начальной буквой английского слова All — «все»). Термин «некоторые х» или «существует хотя бы одно значение x» обозначается через и называется квантором существования (символ есть перевернутая буква Е, являющаяся первой буквой английского слова Exist — «существовать»).

Выставляя кванторы перед предикатами, мы как бы усиливаем или ослабляем их действие. Так, выражение

означает «для всех без исключения х свойство Р истинно», а выражение

означает «существует по крайней мере одно значение х, для которого свойство Р истинно». Мы не будем использовать так называемые свободные переменные, т.е. не будем рассмат-ривать предикатные функции, аргументы которых не связаны ни квантором общности, ни квантором существования. Сказать «для всех х свойство Р истинно» — это все равно, что сказать «конъюнкция всех значений предикатной функции равна единице»:

Квантор существования означает дизъюнкцию всех значений предикатной функции:

3. Оба квантора можно отрицать и выражать один через другой на основе закона де Моргана:

Отсюда

Осмыслить формулы отрицания кванторов поможет следующий пример. Пусть предикат означает, что «х является простым числом». Когда х будет пробегать ряд натуральных чисел —

предикатная функция пробежит ряд истинных и ложных значений

Убедимся в справедливости первой формулы для отрицания квантора общности:

= «не все х простые числа» = «существуют такие х, которые являются непростыми числами» =

Оба эти высказывания истинны. Теперь убедимся в справедливости второй формулы для отрицания квантора существования:

= «нет ни одного х, которое было бы простым» == «все х являются непростыми числами» = Эти высказывания — ложны.

4. Пусть предметная область предиката Р(x) состоит всего из двух конкретных значений а и b . .Учитывая, что

составим таблицу, из которой непосредственно вытекают три элементарных клаузы:

Вместо в последних выражениях можно было бы взять — семантика клауз от этого не изменится, а она такова: если выражение «для всех х свойство Р выполняется» является истинным, то для конкретного значения х, равного а, это свойство тоже будет выполняться. Первая клауза является предикатной формой выражения аксиомы порядка:

Р(а)	Р(Ь)	Vx P{x)	Эх Р(х)
0	0	0	0
1	0	0	1
0	1	0	1
1	1	1	1

Действие ее продемонстрируем на уже знакомом нам примере, который сейчас мы сформулируем более отчет-ливо:

Для всех х справедливо правило: если х — человек, то х смертен. Сократ человек. Следовательно, Сократ смертен.

Введем два предиката:

Примем также, что а = «Сократ». Составим клаузу, соответствующую нашей легенде:

Для ее доказательства достаточно перенести вторую посылку вправо за знак метаимпликации, чтобы клауза сразу же удовлетворяла аксиоме порядка в предикатной форме:

Ясно, что второй пример с заключением о гениальности Сократа является ложным выводом, поскольку приводит к клаузе, противоречащей аксиоме порядка:

5. Конъюнктивная природа квантора общности и дизъюнктивная квантора существования с точки зрения отношения эквивалентности накладывают определенные ограничения при использовании их совместно с дизъюнкцией и конъюнкцией как логическими операциями.

Пусть для определенности предметная область состоит из двух элементов а и b (в общем случае для областей, состоящих из n элементов, все представленные здесь доказательства останутся теми же, только окажутся более громоздкими). Убедимся, что следующие два тождества выполняются:

Действительно,

Аналогично расписывается второе равенство.

Однако ситуация изменится, если квантор общности использо-вать совместно с дизъюнкцией, а квантор существования — с конъюнкцией:

В самом деле,

Первая клауза верна, так как она сводится к аксиоме порядка:

Аналогично доказывается клауза —

6. В логике предикатов, как и в логике высказываний или логике Буля, действует принцип двойственности. Клауза останется в силе, если ее посылки и заключения поменять местами, но при этом одновременно произвести замену:

Благодаря этому принципу последнюю клаузу можно не доказывать отдельно, а составить, исходя из истинности предыдущей.

Установленное свойство кванторов в отношении дизъюнкции отражается и на импликации, поскольку она может быть выражена через дизъюнкцию. Поэтому справедливы следующие выражения:

Но ситуация вновь изменится в пользу отношения эквивалент-ности, если любой из двух предикатов заменить высказыванием:

Действительно,

Раскрывая скобки и используя закон идемпотентности и поглощения, или применяя вновь принцип двойственности, можно доказать второе равенство. Отсюда будут выполняться и равенства для импликации:

*

Чтобы сохранить отношение эквивалентности при вынесении за скобки квантора при конъюнкции и квантора при дизъюнкции, когда даны два различных предиката, прибегают к введению дополнительной переменной, например:

Аналогично поступают в других случаях

Последний пример показывает, что кванторы и можно переставлять местами, если они независимы (в данном случае они относятся к независимым одноместным предикатам).

Рассмотрим всевозможные комбинации кванторов при двухместных предикатах. С помощью законов коммутативности и ассоциативности для конъюнкции и дизъюнкции доказывается справедливость двух тождеств:

т.е. одинаковые кванторы при двухместных предикатах можно переставлять местами. Но перестановка кванторов и подчинена только отношению порядка:

В самом деле,

где

Таким образом, исходная клауза свелась к аксиоме порядка —

7. Справедливость последней клаузы можно установить и с помощью таблицы истинности, в которой приняты следующие сокращения:

На основе этой же таблицы можно установить истинность множества других клауз (к и т принимают значения а или Ь):

Р(а, а)	Р(э, Ь)	Р(Д а)	Р(Д ь)	VVP	3VP	V3P	33 Р
0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	1
0	1	0	0	0	0	0	1
1	1	0	0	0	1	1	1
0	0	1	0	0	0	0	1
1	0	1	0	0	0	0	1
0	1	1	0	0	0	1	1
1	1	1	0	0	1	1	1
0	0	0	1	0	0	0	1
1	0	0	1	0	0	1	1
0	1	0	1	0	о	0	1
1	1	0	1	0	1	1	1
0	0	1	1	0	1	1	1
1	0	1	1	0	1	1	1
0	1	1	1	0	1	1	1
1	1	1	1	1	1	1	1

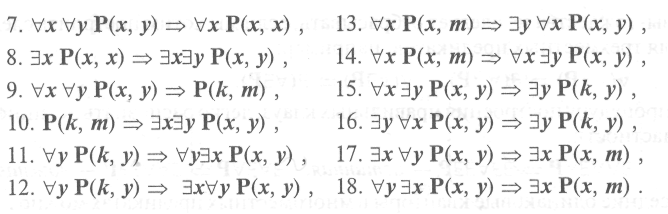
Пять первых клауз из приведенного списка являются для нас сейчас особенно важными, так как они дают ключ к пониманию процедуры составления истинных клауз для многоместных предикатов с любым числом кванторов. Эту проце­дуру схематично можно пояснить следующим образом. Для одноместных предикатов справедливы три клаузы:

Клауза

является ошибочной. Для двухместных предикатов будут верны уже девять клауз, четыре из которых являются тождествами, а пять других как раз и возглавляют приведенный список:

Клаузы-тождества не следует отбрасывать, если мы хотим построить следующий ряд для трехместных предикатов, например:

Зная процедуру построения правильных клауз, легко распознать истинность клауз, в частности:

Соседние одинаковые кванторы в многоместных предикатах можно переставлять в любом направлении; что же касается различных кванторов, то здесь допустима лишь перестановка, описанная клаузой 6 в вышеприведенном списке:

Клаузы-тождества не следует Отбрасывать, если мы хотим построить следующий ряд для трехместных предикатов, например

Зная процедуру построения правильных клауз, легко распознать истинность клауз, в частности:

Соседние одинаковые кванторы в многоместных предикатах можно переставлять в любом направлении; что же касается различных кванторов, то здесь допу­стима лишь перестановка, описанная клаузой 6 в вышеприведенном списке:

Одинаковые кванторы могут быть объединены по схеме, продиктованной клаузами 7 и 8:

Законы конкретизации, представленные в списке следующими десятью клаузами (с 8 по 18) и являющиеся производными от первых шести клауз, естественно, распространяются и на многоместные предикаты.

В отношении дизъюнкции и конъюнкции двух многоместных предикатов действуют примерно те же законы эквивалентности, что и для одноместных. Если все кванторы соответствуют операции, то введение дополнительных пере­менных необязательно, например:

Во всех остальных случаях необходимо вводить переменные:

Формализм теории предикатов, конечно, будет неполным без рассмотрения операции отрицания многоместных предикатов. Для понимания существа дела достаточно привести одно доказательство для двухместного предиката:

Отсюда вытекает простое правило перемещения символа отрицания слева направо для многоместных предикатов, например:

Таким образом, чтобы произвести полное отрицание многоместного предиката с кванторами, необходимо прибегнуть к замене:

8. Процедура составления истинных клауз из предикатов с кванторами, описанная в предыдущем подразделе, позволяет построить булеан из кванторов (рис. 16).

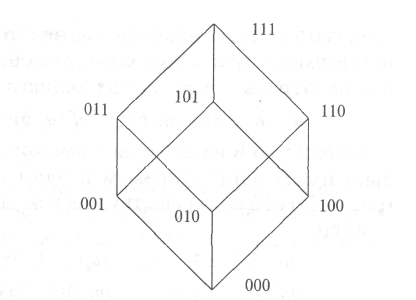
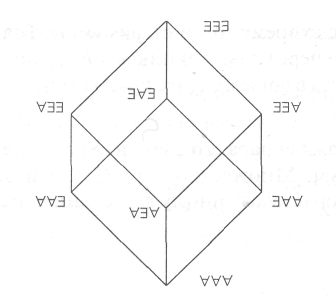
Рис. 16. Рис. 17.

Булеан — это очень распространенный математический объект. Так, если в кванторном булеане все символы заменить на 0 и — на 1, то получим булеан на 0,1-векторах (рис. 17). Если дано множество из элементов — а, b, с, то все его подмножества образуют точно такой же булеан (рис. 18). Наконец, приведем пример из арифметики: делители числа 30 образуют аналогичный булеан (рис. 19).

Булеан есть частично упорядоченное множество, на котором действуют законы логики множеств. Чтобы раскрыть его свойства, введем несколько определений.

Множество элементов любой природы называется линейно-упорядоченным, если любые два его элемента а и Ъ связаны отношением порядка — либо , либо . Множество называется частично упорядоченным, если имеются по крайней мере два несопоставимых элемента, на которые не распространяется от­ношение порядка.

Верхней границей подмножества называют такой элемент , что для всех справедливо отношение порядка . Нижней границей подмножест­ва i называют такой элемент что для всех справедливо отноше­ние , Наименьшая верхняя граница называется супремумом (sup Q), а наибольшая нижняя граница — инфимумом (infQ). Помимо супремума и инфимума, вводятся понятия точной верхней грани и точной нижней грани, которые могут

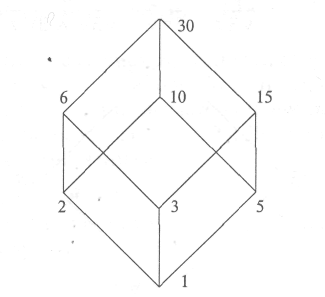
Рис. 18 рис. 19

совпадать или не совпадать, соответственно, с супремумом и инфимумом. Точную верхнюю грань двух элементов обозначим через дизъюнкцию , точную нижнюю грань — через конъюнкцию Тогда в общем случае будем иметь:

Множество R называется решеткой, если каждая пара его элементов обязательно имеет один супремум и один инфимум. Множество , , и (рис. 20) образует решетку, так как удовлетворяет указанному требованию, на­пример:

Множество а, Ь, с, d (рис.21) не образует решетки, так как а и b имеют два инфимума и ни одного супремума, элементы c u d имеют два супремума и ни одного инфимума.

Решетка называется булевой или булеаном, если ее элементы удовлетворяют законам булевой логики — коммутативности, ассоциативности, дистрибутивности, нуля и единицы. Для кванторных решеток все четыре закона выполняются:

■

Поскольку в кванторном булеане предполагаются только положительные предикаты, т.е. отсутствуют обратные элементы, типа , то и в законе для нуля и единицы отсутствуют равенства, отражающие взаимное дополнение эле-' ментов. Однако вместо и можно взять полностью нулевой и единичный векторы, тогда уже все законы нуля и единицы будут выполняться, например:

Если для кванторов справедливы аксиомы логики множеств, то на них дол­жны распространиться и все выводимые из них тождества, например, закон де Моргана:

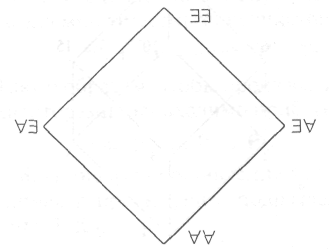
Рис. 20 рис. 21

Аксиома порядка, которая может быть выражена клаузами:

также имеет место в логике предикатов. На первый взгляд выражения типа

противоречат аксиоме порядка. Однако подобные клаузы всегда заменимы тождествами, поэтому их можно представить аксиомой порядка. Тождества возникают для линейно-упорядоченных элементов, каковыми и являются элементы и

Несопоставимые же элементы, к которым относятся, например, элементы и , уже не будут описываться тождествами, а только отношением порядка:

Так как

в логике предикатов будут возникать совершенно специфические клаузы, не сводящиеся к аксиоме порядка, типа —

9. Рассматривая булеаны, нельзя не упомянуть о законе четырехполюсника. Действие его продемонстрируем сначала на числовом булеане делителей числа 30 (см. рис. 17). Если наибольший общий делитель (НОД) двух чисел а и Ъ обо­значить конъюнкцией ( ), а наименьшее общее кратное (НОК) — через дизъюнкцию ( ), то в отношении этих двух арифметических понятий будут действовать все четыре закона булевой логики. Убедимся в справедливости закона ди­стрибутивности:

при а=6, b=10 и c=5 получим: , или , или10 = 10.

Но из арифметики известен закон: произведение любых двух чисел равно произведению

их НОД и НОК: .

В частности,

Этот арифметический закон является прямым следствием булеановой структуры делителей чисел. Подобный закон имеет место в любом булеане (хотя смысл операций в нем может существенно меняться) и называется он законом четырехполюсника. Четыре полюса, соответствующие числам 6,10,2 и 30, взятые на булеане подмножеств (рис. 22), связаны соотношением:

Под символом понимается прямое сложение множеств, при котором повторяющиеся элементы не удаляются. В результате получим:

Закон четырехполюсника выполняется и для 0,1-векторов (рис. 22). Роль прямого сложения здесь заменяется на обыкновенное сложение единиц:

Число единиц в 0,1-векторе а будем называть его модулем или длиной и обозна­чать | а |. Из таблиц (см. выше) выпишем в символической форме модули предикатных векторов

Нетрудно убедиться в справедливости закона четырехполюсника для двухмерного предикатного булеана:

Таблица истинности для трехместных предикатов будет уже состоять из 256 строк. Чтобы определить модули 0,1-векторов кванторного булеана, таблицу истинности можно и не строить, но провести тщательный комбинаторный анализ. В итоге получим:

Кванторный булеан 3-го порядка наложен на векторный булеан 256-го порядка, причем его нижняя точка совпадает не с нулевым вектором, а с вектором первого уровня (00...01), верхняя же точка лежит на предпоследнем уровне (01. ..11). Таким образом, кванторный булеан оказывается немного развернутым относительно векторного булеана. Тем не менее, закон четырехполюсника для него тоже выполняется, в частности:

Вообще, величина модуля вектора а является важной собственной характеристикой клауз, например:

и тождеств, например: 57 = 57 для закона дистрибутивности:

С помощью модулей можно осуществлять частичную проверку правильности логических действий, хотя в случае многоместных предикатов для такого контроля понадобится уже компьютер, поскольку величина модулей даже для четырехместных предикатов исчисляется сотнями тысяч: