1.9.6.1. Минимальные и максимальные элементы множества

Пусть А – частично упорядоченное множество: .

Элемент aA называется максимальным, если не существует больших элементов: из а  х следует х = а.

Элемент аА называется наибольшим, если х  а для .

Элемент аА называется минимальным, если не существует меньших элементов: из х  а следует х = а.

Элемент аА называется наименьшим, если а  х для .

Наибольший элемент часто называют единицей, а наименьший – нулём множества U.

Пример1. Пустое множество  является минимальным элементом булеана по включению.

Пример2. Линейно упорядоченное множество имеет наименьший элемент 0, но не имеет наибольшего элемента.

Пусть – частично упорядоченное множество, B-подмножество А.

Элемент аА называется верхней гранью множества В, если b  a для всех bB.

Элемент аА называется нижней гранью множества В, если a  b для всех bB.

Пример3. Рассмотрим частично упорядоченное множество и интервал B=(0, 1]. Тогда любое число является верхней гранью, а любое число - нижней гранью множества B.

Элемент аА называется точной верхней гранью (супремумом) множества В (обозначается supB), если а – наименьшая из верхних граней множества В.

Элемент аА называется точной нижней гранью (инфимумом) множества В (обозначается infB), если а – наибольшая из нижних граней множества В.

В примере: supB=1, infB=0.

Теорема: Во всяком частично упорядоченном конечном не пустом множестве существует как минимальный элемент, так и максимальный (без док–ва),

Линейный порядок  на множестве А называется полным, если каждое непустое подмножество множества А имеет наименьший элемент. Пара , в которой отношение  является полным порядком на множестве А, называется вполне упорядоченным множеством.

Пример1. Пара не является вполне упорядоченным множеством, т. к., например, полуоткрытый интервал , являющийся подмножеством [0, 1], не содержит наименьшего элемента.

Пример2. Пара является вполне упорядоченным множеством.

Замечание. В полне упорядоченное конечное множество содержит один минимальный элемент, а в произвольном частично упорядоченном конечном множестве их может быть несколько.

Теорема: Всякий частичный порядок на конечном множестве может быть дополнен до линейного (без док–ва).

Замечание: В данном случае «может быть дополнен» означает, что существует отношение полного порядка, которое является надмножеством заданного отношения частичного порядка.

Аксиомы частичного порядка могут быть записаны тогда привычным образом:

1. x ≤ x для всех x M

2. Если x ≤ y и y ≤ x, то x = y

3. Если x ≤ y и y ≤ z, то x ≤ z

Пример3. Обычное отношение ≤ является частичным упорядочением множества всех положительных целых чисел.

Пример4. Отношение (m дели n) – другое частичное упорядочение на множестве положительных целых чисел.

Пример5. Для любого множества Ω отношение является частичным порядком на множестве P(Ω) всех подмножеств множества Ω.

1.9.6.2. Диаграммы Хассе

Рассмотрим множество А с заданным на нём отношением частичного порядка .

Говорят, что элемент у покрывает элемент х, если х  у и не существует такого элемента z, что x < z < y.

Если множество А конечно, то частично упорядоченное множество можно представить в виде схемы, называемой диаграммой Хассе. В ней каждый элемент

изображается точкой на плоскости. Если у покрывает х, то точки х и у соединяют отрезками, причём точку, соответствующую х, располагают ниже у.

Пример1. Рассмотрим частично упорядоченное множество , где A={1, 2, 3}. Множество P(А) содержит восемь элементов:

{0, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}. (рис. 5а)

Пример 2. Пусть А={1, 2, 3, 4, 5, 6, 10, 15, 30}. Отношение частного порядка  на множестве А задаётся по правилу: делится на х (рис. 5б).

На рис.1в изображена диаграмма Хассе линейно упорядоченного множества {0, 1, 2, 3, 4, 5, 6, 7}.

Правило чтения диаграмм Хассе состоит в том, что , если можно прийти из точки х в точку у, следуя вдоль восходящих отрезков, соединяющих точки. Смена направления движения разрешается только в точках диаграммы.

в)

Р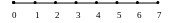 ис.5

Замечание. Диаграммы Хассе первых двух отношений совпадают. Это означает, что эти частично упорядоченные множества имеют одинаковую структуру, причём она отличается от структуры третьего множества, тоже имеющее восемь элементов.

Формально общность структур (рис. 5а и б) определяется понятием изоморфизма.

С помощью диаграмм Хассе поясним понятия верхней и нижней грани для элементов х и у из множества .

На языке диаграмм Хассе означает, что существует путь из х в у. Верхняя грань х и у – это вершина, в которую есть путь из х и у. нижняя грань – это вершина, из которой есть путь и в х, и в у.

Очевидно, что (рис. 5а) и {1, 2, 3} для , т. е. 0 есть наименьший элемент, а {1, 2, 3} – наибольший для частично упорядоченного множества P(A).

В общем случае для некоторых элементов верхняя и нижняя грань может быть не единственной, причём различные верхние (нижние грани) могут быть несравнимы.

Пример 3. На рис.6а изображена диаграмма Хассе множества

, у которого элементы x₄ , x₅ не имеют верхней грани, а элементы x₂ и x_{3 -} нижней грани.

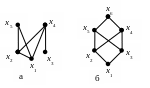
Рис.6.

На рис.6б изображена диаграмма Хассе множества , у которого все элементы не имеют верхней и нижней грани, однако, например, x₁ и x₃ имеют несравнимые верхние грани.