книги / Решение частных задач оптимизации для инженерных систем зданий

Если функция F(x) – квадратичная и строго выпуклая, то все три формулы дают одинаковый результат. Если F(x) – произвольная функция, то каждой из формул cоответствует своя модификация метода сопряженных градиентов. Третья формула использует-

ся редко, так как она требует, чтобы функция F(x) C2 (Rn ) и вы-

числения гессиана функции F(x) производилось на каждом шаге метода.

Анализ метода

Если функция F(x) неквадратичная, метод сопряженных градиентов может и не сходиться за конечное число шагов. Кроме того, точное вычисление αk на каждом шаге возможно только в редких случаях. Поэтому накопление погрешностей приводит к тому, что векторы pk перестают указывать направление убывания функции F(x). Тогда на каком-то шаге полагают βk = 0. Совокупность всех номеров k, при которых принимается βk = 0, обозначим за I0 .

Номера k I0 называются моментами обновления метода. На практике часто выбирают I0 ={n, 2n,3n,...}, где n – размерность

пространства.

Сходимость метода

Для метода Флетчера–Ривса существует теорема о сходимости, накладывающая не слишком жесткие условия на минимизируемую функцию F(x).

Теорема

Пусть F(x) C1 (Rn ) и выполняются следующие условия: 1. αk удовлетворяет строгим условиям Вольфа:

F (xk −1 +αk pk ) ≤ F (xk −1 ) +c1αk F′(xk −1 ), pk ,

21

F′(xk −1 +αk pk ), pk ≤ c2 F′(xk −1 ), pk ,

где 0 < c1 < c2 < 12.

2.Множество M ={x F(x) ≤ F (x0 )} ограничено.

3.Производная F′(x) удовлетворяет условию Липшица с константой L в некоторой окрестности N множества M:

F′(x1 ) − F′(x2 ) ≤ Lx1 − x2 , x1, x2 N.

Тогда

Для метода Полака–Райбера доказана сходимость в предположении, что F(x) – строго выпуклая функция. В общем случае доказать сходимость метода Полака–Райбера невозможно. Напротив, верна следующая теорема.

Теорема

Предположим, что в методе Полака–Райбера значения αk на каждом шаге вычисляются точно. Тогда существует

функция F R3 → R, и начальное приближение x0 такие, что δ > 0,

k = 0, 1, 2, ... f (xk ) > δ.

Тем не менее на практике метод Полака–Райбера работает лучше. Наиболее распространенные критерии останова на практике:

–норма градиента становится меньше некоторого порога;

–значение функции в течение m последовательных итераций почти не изменилось.

Вычислительная сложность

На каждой итерации методов Полака–Райбера или Флетчера– Ривса по одному разу вычисляются функция F(x) и ее градиент

F′(x), решается задача одномерной оптимизации F (xk −1 +αk pk ) →

22

→min. Таким образом, сложность одного шага метода сопряжен-

αk ≥0

ных градиентов имеет тот же порядок, что и сложность шага метода скорейшего спуска. На практике метод сопряженных градиентов показывает лучшую скорость сходимости.

Заключение

В методе сопряженных градиентов используется информация только о линейной части приращения в точке, как и в методах градиентного спуска. При этом метод сопряженных градиентов позволяет решать квадратичные задачи за конечное число шагов. На многих других задачах метод сопряженного градиента также превосходит метод градиентного спуска. Сходимость метода градиентов существенно зависит от того, насколько точно решается задача

цикливания метода устраняются с помощью обновлений. Тем не менее, если метод попадет в локальный минимум функции, скорее всего, ему не удастся из него выбраться.

2.2.Описание метода решения IOSO

Вкачестве программного комплекса для решения задач многокритериальной многопараметрической нелинейной оптимизации инженерных систем зданий может быть применен IOSO NМ [61, 62].

Особенностью данного комплекса является совместимость с Microsoft Excel и другими программами. Эмпирически полученные данные формируются в Excel. В программе IOSO устанавливаются управляемые и неуправляемые параметры, критерии оптимальности, ограничения на параметры процесса. Далее программа IOSO формирует оптимальные параметры процесса методом подбора из Excel.

Предварительная процедура IOSO заключается в формировании начального плана эксперимента, которое может осуществляться как пассивным способом (использование информации о варьируемых параметрах, критериях оптимизации и ограничениях, по-

23

лученной ранее), так и активным способом, когда множество генерируется в начальной области поиска в соответствии с заданным законом распределения. Для каждого вектора варьируемых параметров значения критериев оптимизации и ограничений определяются посредством прямого обращения к математической модели исследуемого объекта. Количество точек, составляющих начальный план эксперимента, зависит от размерности задачи и выбранного варианта функций аппроксимации.

Базовый алгоритм оптимизации схематично может быть представлен в виде следующей последовательности шагов:

Шаг 1. Из текущего плана эксперимента выбираются все различимые по критерию Парето-оптимальные точки: подмножество A.

Шаг 2. Из подмножества A случайным образом выбирается одна Парето-оптимальная точка.

Шаг 3. Строится подмножество плана эксперимента, которое состоит из M точек, ближайших к точке по линейной метрике. Определяется текущая область поиска, которая является замыканием подмножества.

Шаг 4. В текущей области поиска B строятся функции, аппроксимирующие частные критерии оптимизации, и ограничиваемые параметры.

Шаг 5. В текущей области поиска B решаются m задач оптимизации функций аппроксимации. Результатом этого шага являются m точек, в которых ожидаются экстремальные значения частных критериев оптимизации для текущей области поиска.

Шаг 6. В точках находятся истинные значения частных критериев оптимизации посредством прямых обращений к математической модели исследуемого объекта. Точки включаются в план эксперимента.

Шаг 7. Проверка стоп-критерия. Шаг 8-а. Переход к шагу 1.

Шаг 8-б. В окрестности текущей Парето-оптимальной точки по нормальному закону генерируется n точек. Точки включаются в план эксперимента. Переход к шагу 1.

24

Важно подчеркнуть, что на начальной стадии процесса оптимизации точность функций аппроксимации может быть весьма незначительной из-за небольшого количества точек в плане эксперимента и сравнительно большой текущей области поиска. Однако по мере решения задачи количество точек в плане эксперимента, находящихся в окрестности искомых Парето-оптимальных точек, возрастает. В то же время уменьшается размер текущей области поиска. Эти тенденции приводят к увеличению точности функции аппроксимации и, следовательно, к повышению эффективности работы алгоритма оптимизации. Фактически в процессе оптимизации происходит постоянное накопление информации об исследуемом объекте и использование этой информации для определения направления дальнейшего поиска.

Для повышения эффективности предлагаемого метода оптимизации разработан ряд эвристических процедур. Эти процедуры направлены на адаптивное изменение максимального количества точек в плане эксперимента; количества точек в текущей области поиска M; величины дисперсии нормального закона распределения и на рациональный выбор шагов 8-а или 8-б базового алгоритма оптимизации.

Основные преимущества алгоритма IOSO перед известными подходами к решению многокритериальных задач заключаются в возможности решения практических задач для случая невыпуклых, недифференцируемых и стохастических целевых функций и ограничений; в отсутствии необходимости значительной адаптации математической модели исследуемого объекта; в возможности получения множества Парето-оптимальных решений при сравнительно небольшом количестве прямых обращений к исследуемой математической модели; в достаточно высокой вероятности определения глобального экстремума в многоэкстремальных задачах. Эти преимущества являются основой для широкого использования предлагаемого метода для решения практических задач.

25

Глава 3

РЕШЕНИЕ ЧАСТНЫХ ЗАДАЧ ОПТИМИЗАЦИИ. РАЗРАБОТКА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ ИНЖЕНЕРНЫХ СИСТЕМ ЗДАНИЙ И СООРУЖЕНИЙ

3.1. Разработка математической модели оптимизации теплоотдающего элемента (ребра) теплообменного аппарата

3.1.1. Техническая и математическая постановка задачи исследования

Проведен обзор существующих критериев оптимальности параметров теплообменных аппаратов систем воздушного отопления зданий для оценки эффективности их функционирования и ресурсоэффективности конструкций. Поиск критерия оптимальности для конкретных условий представляет собой достаточно сложную комплексную задачу [55, 65–68].

Основные характеристики теплообменных аппаратов, такие как теплоотдача, площадь теплообмена, металлоемкость и стоимость аппарата, зависят от размеров оребрения, поэтому оптимальная высота ребра во многом определяет совершенство конструкции.

Для оценки оптимальности параметров ребра теплообменных аппаратов предложено использовать показатель эффективности ребра, разработанный Бесселем [56]:

трубы, м; r0′ – радиус оребрения, м; J1, K1, J0, K0 – модифицированные функции Бесселя.

26

Данный показатель использован в работе для оценки эффективности разработанного оптимального размера ребра теплообменного аппарата.

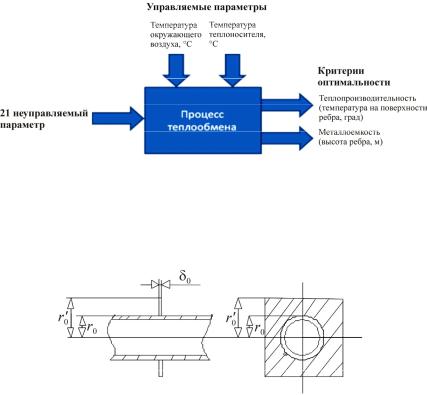
Для нахождения минимальной массы ребра теплообменного аппарата при максимальной его теплопроизводительности разработана математическая модель многокритериальной задачи оптимизации параметров теплоотдающих элементов теплообменных аппаратов систем воздушного отопления зданий, которая решена с помощью метода нелинейной оптимизации [29–33] (рис. 4).

Рис. 4. Схема постановки математической модели процесса теплообмена на ребре

Математическая модель строилась для наружной поверхности радиального ребра прямоугольного профиля (рис. 5).

Рис. 5. Радиальное ребро прямоугольного профиля: r0 – радиус несущей трубы; r0′ – радиус трубы с оребрением; δ0 – толщина ребра

27

3.1.2. Выбор критериев оптимизации, управляемых и неуправляемых параметров, граничных условий

Температура на поверхности ребра определяет теплопроизводительность, а высота ребра – металлоемкость теплообменного аппарата, поэтому в качестве критериев оптимальности выбраны:

1)x – температура на поверхности ребра (J1);

2)y – высота ребра (J2).

Вкачестве неуправляемых параметров приняты: радиус несущей трубы, толщина ребра, теплопроводность ребра, расположение пучка в теплообменном аппарате, шаг ребра, количество ребер, число Нуссельта для воздуха, число Рейнольдса для воздуха, коэф-

фициент теплоотдачи от стенки к воздуху и др. – x1 … x21. В работе проведена оценка влияния данных параметров на процесс теплообмена.

Вкачестве управляемых параметров выбраны температура ок-

ружающего воздуха, температура теплоносителя (U1 … U2) как наиболее влияющие на процесс теплообмена. В процессе теплообмена происходит обмен между теплом воды и окружающей средой, которые зависят от параметров воды и воздуха. Параметры, характеризующие эти изменения, находятся в допустимых пределах, установленных для данного процесса.

Зависимости критериев оптимальности и параметров процесса можно записать в следующем виде:

J1 = J1 (x1, ... x21;U1,U2 ) → mах, (22) J2 = J2 (x1, ... x21;U1,U2 ) → min.

Ограничения, накладываемые на параметры процесса, находятся в пределах:

28

Число Нуссельта для турбулентного режима движения воздуха

где hр – шаг ребра, м; dн – наружный диаметр трубы, м; h – высота ребра, м; Reв – число Рейнольдса для воздуха.

Приведенный коэффициент теплоотдачи

где α2 – коэффициент теплоотдачи, Вт/(м² °С); θ0 – разность между температурами поверхностей ребер и воздуха; θ1 – разность между температурами основной поверхности трубы и воздуха; Fп – площадь поверхности между ребрами, м2; Fpc – площадь оребренной поверхности, м2; Fр – площадь ребер, м2 [28].

Общее решение определяется соотношением

Постоянные K1, K0 , J0 , J1 вычисляются в соответствии с гра-

ничными условиями, описанными выше. Используя (30), находим

Вычислив С1, С2, находим распределение температуры по высоте ребра для радиального ребра прямоугольной формы (°С):

где θ0 – температура на поверхности несущей трубы, °С.

30