
книги / Проектирование и исследование идентификационных моделей управляющих систем реального времени
..pdfисключая из рассмотрения все внутренние переменные, являющиеся входными или выходными сигналами внутренних звеньев, можно найти дифференциальное уравнение, описывающее взаимосвязь входной и выходной величин системы иявляющееся, по сути, агрегированной моделью.
Агрегированная модель описывает функциональные взаимосвязи между входными и выходными величинами без учета внутренней структуры и взаимосвязей в системе.
11. Параметрические и непараметрические. Параметрические мо-
дели описываются заданными в явной форме аналитическими зависимостями, содержащими параметры, подлежащие идентификации. Эти зависимости представляют собой параметрические модели конечной размерности, например дифференциальные уравнения определенного порядка, модели в пространстве состояний. Параметрами являются численные значения величин, определяющих выход модели (например, значения коэффициентов обыкновенных дифференциальных уравнений, начальных условий, коэффициентов передаточных функций). Методами параметрической идентификации определяются неизвестные коэффициенты уравнения объекта или передаточной функции.
Непараметрические модели сводятся к описанию преобразований сигналов пространства входов в элементы пространства выходов. В этом случае модель объекта определяется оператором преобразования функций входных сигналов в функции выходных величин. Непараметрическими моделями являются весовые функции, передаточные функции (если заранее не задано число коэффициентов), корреляционные функции, спектральные плотности, ряды Вольтерра. Например, для модели в виде весовой функции связь между входными и выходными сигналами для линейных объектов задается с помощью интеграла свертки (интеграла Дюамеля):
|
∞ |
∞ |
|
|
y(t) = |
∫ |
w(t)u(t − τ)dτ = |
∫ u(t)w(t − τ)dτ, |
(2.17) |
|
0 |
|
0 |
|
где w(t) – импульсная переходная (весовая) функция объекта, являющаяся непараметрической моделью линейного динамического объекта.
Методы непараметрической идентификации используются для определения временных или частотных характеристик объектов. По полученным характеристикам далее можно определить передаточную функ-
41
цию или уравнения объекта. Параметрические модели могут приводить к большим ошибкам, если порядок модели не соответствует порядку объекта. Преимущество непараметрических моделей состоит в том, что они не требуют явного знания порядка объекта. Однако в этом случае описание является, по существу, бесконечномерным.
2.4.3. Математическое описание основных классов моделей
Основные классы моделей имеют следующее математическое описание:
1. Статические модели. Статическая характеристика объекта – это зависимость между входными и выходными сигналами в установившемся режиме. Аналитически, в общем случае, уравнение модели статического объекта имеет вид нелинейной функции многих переменных
y = f (u). |
(2.18) |
Во многих практических случаях общую нелинейную функцию (2.18) удается параметризовать некоторым вектором A, тогда эта зависимость принимает вид
y = f (u, A) |
(2.19) |
и задача идентификации сводится к определению неизвестных параметров A.
Частным случаем параметрических моделей [3, 13] являются модели, линейные относительно оцениваемых параметров:
y = a0 + a1u1 +…+ anun . |
(2.20) |
Моделью статического линейного многомерного объекта с n входами и m выходами является система линейных алгебраических уравнений
y1 = a10 + a11u1 + a12u2 +…+ a1nun , |
|
|
y2 |
= a20 + a21u1 + a22u2 +…+ a2nun |
, |
|
|
(2.21) |
|
|
|
|
= am0 + am1u1 + am2u2 +…+ amnun , |
|
ym |
||
где aij – неизвестные параметры модели, подлежащие определению.
42
В векторно-матричной форме система (2.21) имеет вид |
|
Y = A0 + AU, |
(2.22) |
где U и Y – векторы входных и выходных воздействий;
A0 и A – соответственно вектор и матрица коэффициентов моде-
ли, подлежащие идентификации.
Математическое описание (2.20) называется одномерной линейной регрессией, (2.21–1.22) – многомерной линейной регрессией. На практике большинство задач можно свести к линейный регрессии, поэтому идентификация параметров линейной регрессии является важной задачей и будет рассмотрена ниже.
2. Линейные динамические непрерывные параметрические модели.
Такие модели в теории управления могут быть заданы в следующих формах:
– Обыкновенные дифференциальные уравнения n-го порядка:
|
|
a0 |
dn y(t) |
+ a1 |
dn−1 y(t) |
+…+ an y(t) = |
||||||||||||
|
|
|
|
dt |
n |
|
|
|
dt |
n−1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.23) |
||
|
|
|
|
|
dm x(t) |
|
|
dm−1x(t) |
||||||||||
|
|
= b0 |
+ b1 |
+…+ bm x(t), |
||||||||||||||
|
|
dt |
m |
|
dt |
m−1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где ai , b j (i = |
|
, j = |
|
) |
– параметры модели, подлежащие идентифи- |
|||||||||||||
1, n |
1, m |
|||||||||||||||||
кации. Для большинства реальных физически реализуемых систем управления m ≤ n .
– Передаточные функции. Если к дифференциальному уравнению (2.23) задать нулевые начальные условия, то, применяя преобразование Лапласа, получают передаточную функцию линейного объекта в следующем виде:
W ( p) = |
y( p) |
= |
b0 pm + b1 pm−1 +…+ bm |
, |
(2.24) |
|
|
||||
|
x( p) a0 pn + a1 pn−1 +…+ an |
|
|||
где p – комплексная переменная – параметр преобразования Лапласа.
– Уравнения в пространстве состояний. Динамические процессы, наряду с дифференциальным уравнением n-го порядка (2.24), также можно описать системой n обыкновенных дифференциальных уравнений первого порядка:
43
dyi |
(t) |
|
n |
|
m |
|
|
|
|
|
|
|
|
||||||
|
|
= |
∑ aij y j |
+ |
∑ biju j , i = 1, n. |
(2.25) |
|||
dt |
|||||||||
|
j = 1 |
|
j = 1 |
|
|||||
Вводя в описание вектор состояний системы, представим модель в пространстве состояний в следующей матричной форме:
dX(t) |
= AX(t) + BU(t), |
||
|
|
||
dt |
|||
|
(2.26) |
||
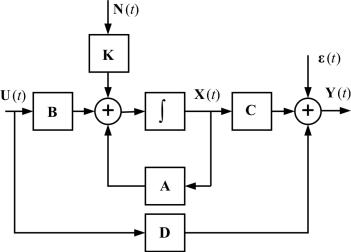
Y(t) = CX(t) + DU(t),
где X(t) – вектор внутренних (динамических) переменных; U(t) – вектор входных переменных;
Y(t) – вектор выходных переменных; A – матрица коэффициентов системы;
B– матрица входа системы;
C– матрица выхода системы;
D– матрица обхода системы.
Сучетом воздействия внешней среды, при наличии входной адди-
тивной помехи N(t) |
и погрешностей измерения ε(t) |
||
ровка модели имеет вид |
|
||
dX(t) |
= AX(t) + BU(t) + KN(t), |
||
|
|
||
dt |
|||
|
|
||
= + + εY(t) CX(t) DU(t) (t),
, базовая формули-
(2.27)
где, помимо рассмотренных ранее обозначений, также присутствуют N(t) – вектор случайных воздействий-помех;
ε(t) – вектор шумов измерения;
K – матрица, описывающая канал прохождения помехи.
Воздействия N(t) и ε(t) , как правило, представляют собой гауссо-
вы случайные процессы в виде белого шума.
Рассмотренная модель (2.27) может быть представлена следующей структурной схемой в пространстве состояний (рис. 2.8).
3. Линейные динамические дискретные параметрические модели.
Эти модели могут принимать следующий вид [10, 21, 22]:
– Обыкновенные разностные уравнения. Универсальной характеристикой для дискретных моделей является разностное уравнение n-го порядка, в котором используется понятие разности как аналога понятию производной для непрерывных моделей:
44
an y(k) + an−1 y(k −1) +…+ a0 y(k − n) = (2.28) = bmu(k) + bm−1u(k −1) +…+ b0u(k − m),
где y(k ), u(k ) – значения выходной и входной величин в k-й момент времени.
Рис. 2.8. Структурная схема линейной динамической системы
впространстве состояния при учете воздействий внешней среды
–Дискретные передаточные функции. Применяя оператор сдвига
во времени z ( y(k + i) = zi y(k )), уравнение (2.28) получают в операторной форме дискретной модели:
W (z) = |
y(z) |
= |
bm |
+ bm−1z−1 +…+ b0 z−m |
. |
(2.29) |
|
|
|
||||
|
x(z) an + an−1z−1 +…+ an z−n |
|
||||
– Уравнения в пространстве состояний. Используя для описания динамики дискретного объекта дискретные переменные состояния, об-
|
x (k ) |
|
|
|
1 |
|
|
разующие n-мерный вектор состояния |
X(k) = x2 |
(k ) |
, получают описа- |
|
|
|
|
|
|
|
|
|
xn |
(k) |
|
ние объекта в пространстве состояний в следующей векторноматричной форме:
45
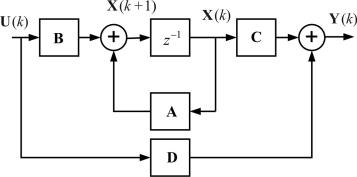
X(k +1) = AX(k) + BU(k),
(2.30)
Y(k ) = CX(k ) + DU(k ).
Структурное представление модели (2.30) приведено на рис. 2.9.
Рис. 2.9. Структурная схема дискретной модели
впространстве состояния
4.Нелинейные динамические модели. Класс нелинейных динами-
ческих систем по сравнению с классом линейных систем значительно шире, так как в этих системах протекают многообразные явления и процессы, не характерные для линейных систем. Вследствие этого для описания таких систем неприменим математический аппарат теории линейных систем, поэтому при решении задачи получения математических моделей нелинейных систем используются два основных подхода [19, 23]. Один подход заключается в получении приближенного математического описания линеаризованной модели с помощью методов линеаризации: гармонической, статистической, малых приращений. Наиболее применим такой подход для объектов, имеющих гладкие характеристики, и процессов, протекающих при небольших отклонениях и возмущенияхотносительно номинальных режимов функционирования.
При втором подходе математическая модель рассматривается как существенно нелинейная. В этом случае наиболее распространенными видами моделей являются следующие:
– Нелинейные дифференциальные уравнения. Для непрерывного одномерного объекта управления связь между входным и выходным сигналами записывается в общем виде неявным выражением
F ( y, |
dy |
, …, |
dn y |
, u, |
du |
, …, |
dmu |
) = 0 , |
(2.31) |
dt |
dt n |
dt |
|
||||||
|
|
|
|
dt m |
|
||||
46
где F – некоторый нелинейный оператор, который требуется идентифицировать. Если возможно, то проводится параметризация нелинейной модели (2.31) на основе структурирования F с введением некоторого вектора параметров А:
F ( y, |
dy |
, …, |
dn y |
, u, |
du |
, …, |
dmu |
, A) = 0. |
(2.32) |
|
dt |
dt n |
dt |
dt m |
|||||||
|
|
|
|
|
|
В этом случае задача идентификации сводится к определению оператора F и оцениванию его вектора параметров A.
Для нелинейного дискретного объекта строятся аналогичные нелинейные разностные уравнения.
– Модели Гаммерштейна. Такие модели нелинейных инерционных объектов строятся в предположении, что нелинейность и инерционность объекта можно разделить и представить объект в виде последовательной комбинации двух звеньев: нелинейного безынерционого и динамического линейного. Модели «вход-выход» для таких объектов в одномерном стационарном случае могут иметь два варианта описания:
|
∞ |
|
|
y(t) = |
∫ w(τ )F (u(t− τ )) dτ |
|
(2.33) |
|
0 |
|
|
или |
|
|
|
y(t) = |
∞ |
|
|
F ∫ w(τ )u(t− τ )dτ |
, |
(2.34) |
|
|
|
|
|
|
0 |
|
|
где w(t) – импульсная переходная функция линейного звена; F (u) – статическая характеристика нелинейного звена.
Структурное представление моделей объекта для каждого из вариантов описания приведено на рис. 2.10, 2.11.
– Разложение Вольтерра. При данном способе описания зависи-
мость между входом u(t) |
и выходом y(t) |
представляется рядом [5, 7] |
|
t |
t |
t |
|
y(t) = ∫ w1 (τ )u(t− τ )dτ + |
∫ |
∫ w2τ( τ1, 2 )u−(tτ |
1 )u−(tτ τ2 )dτ 1+d 2 …, (2.35) |
0 |
0 0 |
|
|
где w1 (τ), w2 (τ1, τ2 ), w3 (τ1, τ2 , τ3 )… – обобщенные весовые функции (ядра) i-го порядка. Такойряд (2.35) носит название ряда Вольтерра.
47
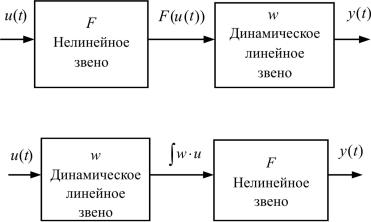
Рис. 2.10. Структурная схема модели Гаммерштейна (2.33)
Рис. 2.11. Структурная схема модели Гаммерштейна (2.34)
Разложение в ряд Вольтерра является непосредственным обобщением линейной модели в форме интеграла свертки на нелинейные объекты. Задача идентификации при этом состоит вопределении обобщенных
весовых функций (ядер): |
w1 (τ), w2 (τ1, τ2 ), w3 (τ1, τ2 , τ3 )…. Для нестацио- |
|||||||
нарного объекта ядра будут зависеть от t . |
|
|||||||
– Описание в пространстве состояний. В общем случае уравнения |
||||||||
состояния для |
конечномерных |
непрерывных систем |
записываются |
|||||
в следующем виде: |
|
|
|
|
|
|
||
|
|
dx(t) |
= f (x(t), u(t), t), |
|
||||
|
|
|
||||||
|
|
dt |
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
(2.36) |
||
|
y(t) = g(x(t), u(t), t), |
|||||||
|
|
|
|
|
|
|
|
|
|
x(t ) = x . |
|
||||||
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
||
В общем случае в уравнениях (2.36) определению подлежат нели- |
||||||||
нейные функции |
f и g . При возможности их параметризации некото- |
|||||||
рым вектором параметров A описание системы принимает вид |
||||||||
|
dx(t) |
= f |
(x(t), u(t), A, t), |
|
||||
|
|
|
dt |
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
(2.37) |
||
|
y(t) = g(x(t), u(t), A, t), |
|||||||
|
|
|
|
|
|
|
|
|
|
x(t ) = x . |
|
||||||
|
|
0 |
|
0 |
|
|
||
|
|
|
|
|
|
|||
48 |
|
|
|
|
|
|
|
|
Уравнения пространства состояний для дискретных нелинейных объектов при параметризации нелинейных функций A имеют вид
x(k +1) = f (x(k), u(k ), A), |
|
|
(2.38) |
y(k ) = g(x(k ), u(k ), A), |
|
|
|
x(k0 ) = x0 . |
|
Представление в пространстве состояний особенно удобно для многомерных объектов. Для нестационарных объектов необходимо ввести зависимость вектора A от времени.
2.4.4. Управляемость, наблюдаемость и идентифицируемость систем
Важными понятиями для исследования систем, в том числе и для идентификации, являются понятия управляемости, наблюдаемости и идентифицируемости систем [4, 7, 11, 12].
Рассмотрим каждое из этих понятий подробнее.
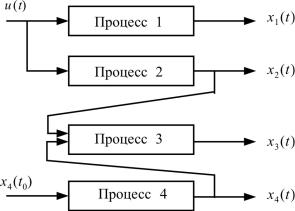
Система является управляемой, если она может быть переведена из любого начального состояния X(t0 ) в любое другое желаемое со-
стояние X(tk ) за конечный интервал времени τ (τ = tk − t0 ) путем задания (изменения) входного воздействия U(t) .
Понятие управляемости можно проиллюстрировать следующим примером (рис. 2.12).
Рис. 2.12. Структурная схема неуправляемой системы
49
Очевидно, что эта система является неуправляемой, так как управляющее воздействие u(t) влияет не на все переменные состояния (пере-
менная состояния x4 (t) не поддается управлению).
Система является наблюдаемой, если все переменные состояния могут быть непосредственно или косвенно определены по выходному вектору системы.
Если управляемость системы требует, чтобы каждое состояние системы было чувствительно к входному воздействию, то наблюдаемость требует, чтобы каждое состояние системы влияло на измеряемый выходной вектор.
Следует различать понятия «измеряемость» и «наблюдаемость». Измерить переменную – значит непосредственно с помощью измерительных устройств зафиксировать значение переменной в текущий момент времени. Наблюдаемая переменная – это либо измеренная, либо вычисленная на основе измеренных переменных переменная.
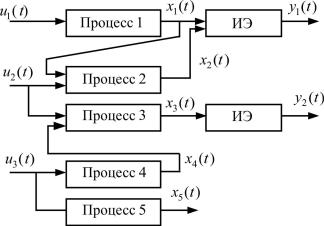
Понятие наблюдаемости можно проиллюстрировать следующим примером (рис. 2.13).
Рис. 2.13. Структурная схема неуправляемой системы
Очевидно, что эта система является ненаблюдаемой, так как не все переменные состояния X(t) могут быть восстановлены на основе выходного измеренного вектора Y(t) (ИЭ – измерительный элемент). Так, динамическая переменная x5 (t) является ненаблюдаемой.
50
