
книги / Проектирование и исследование идентификационных моделей управляющих систем реального времени
..pdf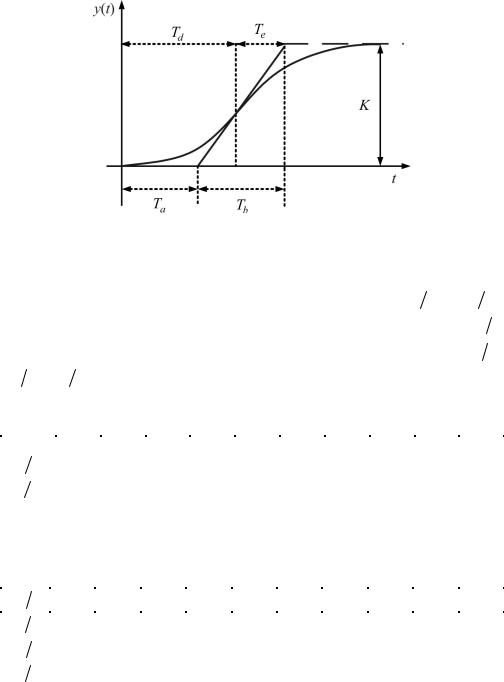
Рис. 2.22. Переходная характеристика апериодического звена высшего порядка
По табл. 2.2 и 2.3 [7] определяются порядок системы n и посто-
янная времени τ. Сначала по табл. 2.2 и по отношениям Ta |
Tb и Te Tb |
|||||||||||||||||||
определяется порядок звена. Далее по n определяется отношение |
Ta |
τ |
||||||||||||||||||
и постоянная времени τ (проверка осуществляется по отношениям Tb |
τ, |
|||||||||||||||||||
Td |
τ и Te τ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
7 |
8 |
|
9 |
|
10 |
|
|
Ta |
Tb |
0,000 |
|
0,104 |
|
0,218 |
|
0,319 |
|
0,410 |
|
0,493 |
0,570 |
0,642 |
|
0,709 |
|
0,773 |
||
Te |
Tb |
1,000 |
|
0,736 |
|
0,667 |
|
0,647 |
|
0,629 |
|
0,616 |
0,606 |
0,599 |
|
0,593 |
|
0,587 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
7 |
8 |
|
9 |
|
10 |
|
|
Ta |
τ |
|
0,000 |
|
0,282 |
|
0,805 |
|
1,425 |
|
2,100 |
|
2,811 |
3,549 |
4,307 |
|
5,081 |
|
5,869 |
|
Tb |
τ |
|
1,000 |
|
2,718 |
|
3,695 |
|
4,463 |
|
5,119 |
|
5,699 |
6,226 |
6,711 |
|
7,164 |
|
5,590 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Td |
τ |
|
0,000 |
|
1,000 |
|
2,000 |
|
3,000 |
|
4,000 |
|
5,000 |
6,000 |
7,000 |
|
8,000 |
|
9,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Te |
τ |
|
1,000 |
|
2,000 |
|
2,500 |
|
2,888 |
|
3,219 |
|
3,510 |
3,775 |
4,018 |
|
4,245 |
|
4,458 |
|
Колебательный объект второго порядка имеет передаточную функцию
71

K |
|
W ( p) = T 2 p2 + 2Tξp +1. |
(2.84) |
Коэффициент усиления определяется аналогично апериодическим звеньям. Для определения приближенных значений постоянной времени Т и коэффициента демпфирования ξ по переходной характе-
ристике с помощью графических методов (рис. 2.23) можно воспользоваться следующими соотношениями:
ξ = |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
, |
(2.85) |
|
|
|
|
π2 |
|
|
|||||||||||
1+ |
|
|
|
|
|
|
|
|
||||||||
|
|
|
A1 |
|
2 |
|
||||||||||
|
|
|
|
|
|
|||||||||||
|
|
ln |
|
|
|
|
||||||||||
|
|
|
A2 |
|
||||||||||||
|
|
|
|
|
|
|
||||||||||
T = T |
|
|
ξ |
|
. |
|
|
(2.86) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
2 ln |
A1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
A2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Идентификация идеального: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
W ( p) = |
K |
|
|
|
|
|
(2.87) |
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|||
и реального: |
|
|
|
|
|
|
|
|
|
|
|
|||||
W ( p) = |
|
|
|
K |
|
|
|
|
(2.88) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
p(Tp +1) |
||||||||||||||||
|
|
|
|
|
||||||||||||
Рис. 2.23. Переходная характеристика колебательного звена
72
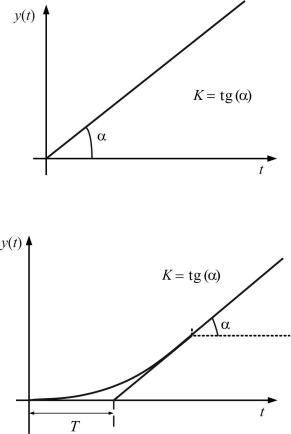
интегрирующих звеньев осуществляется графически (рис. 2.24 – идеальное, 2.25 – реальное).
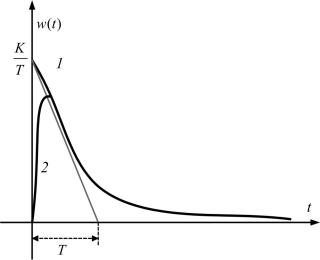
Рис. 2.24. Переходная характеристика идеального интегрирующего звена
Рис. 2.25. Переходная характеристика реального интегрирующего звена
Значение времени запаздывания τ0 в звене чистого запаздывания
W ( p) = e− pτ0 |
(2.89) |
определяется как интервал времени между моментом изменения входного сигнала и началом изменения выходной величины.
2.5.2. Идентификация с помощью импульсной переходной характеристики
Импульсные переходные характеристики w(t) представляют собой реакцию объекта на входящий импульс бесконечно малой длительности
73
и бесконечно большой амплитуды. Импульсная переходная характеристика связана с переходной характеристикой:
w(t) = |
dh(t) |
. |
(2.90) |
|
|||
|
dt |
|
|
Алгоритм идентификации линейных систем с использованием импульсных переходных характеристик аналогичен алгоритму идентификации с помощью переходных характеристик.
На практике точно реализовать импульсное воздействие, близкое по свойствам к идеальному импульсу
δ (t)= |
|
0, |
t ≠ |
0 |
, |
(2.91) |
|
||||||
|
|
∞ , |
t= |
0 |
|
|
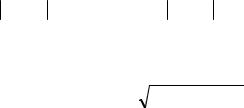
невозможно, что объясняется техническими причинами. Из-за отличий при реализации входного импульса экспериментально снятая импульсная характеристика отличается от теоретической. На рис. 2.26 представлено сопоставление экспериментальной импульсной переходной характеристики 1 апериодического объекта первого порядка и теоретической 2.
При идентификации многомерного объекта для определения его переходной матрицы Wвыхвх (t) или импульсной переходной матрицы
Рис. 2.26. Импульсная переходная характеристика апериодического звена
74
wвых (t) проводится эксперимент с nвх циклами, где nвх – количество
входов. На каждый из входов объекта последовательно во времени с интервалами, превышающими время затухания собственных движений объекта, подаются ступенчатые воздействия или короткие импульсы
для определения Wвыхвх (t) или wвых(t) соответственно. Регистрация реак-
ций на выходах объекта обеспечивает определение всех элементов искомых матричных функций.
2.5.3. Идентификация с помощью частотных характеристик
Частотный метод идентификации линейных систем основан на работах Найквиста и Боде и использует в качестве исходных частотные или спектральные характеристики.
Частотные характеристики объекта включают в себя амплитудночастотную характеристику A(ω) , представляющую зависимость отно-
шения амплитуд гармонических сигналов на входе и выходе объекта от частоты колебаний в установившемся режиме; фазочастотную характеристику φ(ω) , отражающую зависимость сдвига фаз между входными
и выходными гармоническими сигналами от частот.
Частотные характеристики динамических объектов, как правило, определяются в режиме активного эксперимента подачей на вход объекта гармонического сигнала, частота которого изменяется в определенном диапазоне, и регистрации выходной реакции.
Для линейного стационарного объекта вход-выходное соотношение определяется через амплитудно-фазовую характеристику:
|
|
|
y( jω) = W ( jω)x( jω), |
|
(2.92) |
||
где x( jω |
) |
– |
частотный |
спектр |
входного |
сигнала |
объекта, |
x( jω) = ∞∫ x(t)e− jωt dt ; |
|
|
|
|
|||
−∞ |
|
|
частотный |
спектр |
выходного |
сигнала |
объекта, |
y( jω |
) |
– |
|||||
∞
y( jω) = ∫ y(t)e− jωt dt .
−∞
Из формулы (2.92) следует, что амплитудно-фазовую характеристику объекта W ( jω) можно определить экспериментальным путем на
75
основе частотных спектров измеренных входных и выходных сигналов x(t) и y(t) . Основной сложностью при таком подходе является невозможность формирования входного воздействия x(t), частотный спектр которого был бы непрерывным на бесконечном интервале изменения частот ω. Амплитудно-фазовая характеристика объекта W ( jω) также должна быть непрерывной во всей полосе частот, что обеспечить технически практически невозможно, поэтому, вследствие наблюдения сигналов x(t) и y(t) только на ограниченном отрезке времени, возникают
значительные ошибки их измерения.
В соответствии с этим в реальных условиях воздействие полигармонических сигналов в широком диапазоне изменения частот заменяют последовательным применением моногармонических воздействий x(t) = xm sin ωit с разными частотами ω = ωi и исследуют реакцию на
них. На выходе объекта в установившемся состоянии будут наблюдаться гармонические колебания той же частоты:
y(t) = ym (ωi ) sin(ωit + φ(ωi )) . |
(2.93) |
||||
В этом случае амплитудно-фазовая характеристика, представлен- |
|||||
ная в комплексном виде, определяется зависимостью |
|
||||
W ( jω) = |
y( jω) |
= |
ym ( jωi ) |
e jφ(ωi ) = A(ω)e jφ(ω) . |
(2.94) |
x( jω) |
|
||||
|
|
x |
|
||
|
|
|
m |
|
|
Прямые методы получения амплитудной или фазовой частотных характеристик, основанные на непосредственном измерении амплитуды и фазы отклика на синусоидальный сигнал, могут быть использованы в ограниченном числе случаев, когда помехи, искажающие измерения, отсутствуют. В реальных условиях проведения экспериментов объект всегда подвергается воздействию шумов. В этом случае для получения достоверного результата выгоднее использовать другие алгоритмы обработки данных, например методы, основанные на гармоническом анализе сигналов. Эти методы базируются на измерении основной гармоники установившихся колебаний на выходе исследуемого объекта при гармоническом воздействии на входе. Обработка выходного периодического сигнала производится с помощью гармонического анализатора, позволяющего определять параметры одной или нескольких гармоник.
76
Амплитудно-фазовая характеристика объекта представляется в алгебраическом виде:
W ( jω) = A(ω)e jφ(ω) = P(ω) + jQ(ω), |
(2.95) |
где P(ω) = W ( jω) cos φ(ω), Q(ω) = W ( jω) sin φ(ω).
Тогда амплитудно-частотную характеристику и фазочастотную характеристику φ(ω) будут определять по формулам
|
|
|
|
A(ω) = |
P2 (ω) + Q2 (ω), |
(2.96) |
|||||
|
|
|
|
φ(ω) = arctg |
Q(ω) |
. |
(2.97) |
||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
P(ω) |
|
|
Параметры P(ω) |
и Q(ω) можно определить, подавая на вход объ- |
||||||||||
екта тестовый сигнал |
x(t) = xm sin ωit и применяя фильтрацию Фурье |
||||||||||
к выходному сигналу |
y(t) . Такая процедура фильтрации реализуется |
||||||||||
умножением y(t) |
соответственно на sin ωit и на cos ωit |
и усреднением |
|||||||||
по целому числу периодов k : |
|
|
|
|
|
|
|||||
|
|
|
P(ωi ) = |
2 |
|
T |
|
||||
|
|
|
|
|
∫ y(t) sin(ωit)dt, |
(2.98) |
|||||
|
|
x T |
|||||||||
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
Q(ωi ) = |
|
2 |
|
T |
|
|||
|
|
|
|
|
|
∫ y(t) cos(ωit)dt, |
(2.99) |
||||
|
|
|
x T |
||||||||
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
m |
|
|
|
|
|
где T = kT , |
T = |
2π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
i |
i |
ωi |
|
|
|
|
|
|
|
|
|
Положительным свойством таких алгоритмов идентификации является использование неограниченного частотного диапазона, что позволяет применять их также в области низких частот, характерных для рабочих процессов многих промышленных технических объектов.
Для линейного многомерного динамического объекта эксперимент, с помощью которого определяются частотные характеристики, реализуется отдельными циклами, во время которых синусоидальный сигнал с заданной частотой и с заданной амплитудой подается на один вход. После достижения практически установившегося режима вынуж-
77

денных колебаний объекта регистрируются амплитуды и фазы гармонических колебаний на всех выходах и амплитуда и фаза данного ненулевого входного сигнала. Поскольку выходной сигнал всегда зашумлен и обычно искажен нелинейностями, имеющимися в объекте, требуется выделение первой гармонической составляющей.
2.6.СОВМЕСТНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ И СОСТОЯНИЯ
Висследовании систем автоматического управления (САУ) особый интерес представляет класс САУ с ограничениями по измерениям. Анализ известных методов показал, что большинство методов идентификации ориентировано на объекты с полной измеряемостью. Однако на практике полностью измерить переменные состояния не всегда представляется возможным [4, 7, 11, 27]. Так, для многих объектов УС РВ характерна ограниченная измеряемость объекта, что предполагает усложнение алгоритма идентификации и отдельное исследование измеряемого объекта. Для гидромеханических агрегатов, являющихся исполнительными механизмами во многих САУ, основные динамические координаты – перемещения подвижных элементов. Такое выделение целесообразно, поскольку перемещения являются выходными переменными динамических типовых функциональных элементов гидросистем. Однако не все перемещения являются измеряемыми переменными. Конструктивные особенности таких элементов, как золотник или изодрома, не позволяют измерить перемещение хода золотника или изодрома, поскольку поршни этих элементов перемещаются внутри закрытого объема.
Для данного класса объектов задача идентификации сводится к одновременному оцениванию параметров и неизмеряемых координат объекта. Анализ известных методов идентификации [4, 7] показал, что существует несколько подходов к решению поставленной задачи. Наибольший интерес представляет совместное оценивание параметров и состояния.
Совместное оценивание параметров и состояния предполагает расширение вектора состояния за счет неизмеряемых координат.
Пусть объект описывается системой уравнений
dX(t)
dt
=Y(t)
= F (X(t), U(t), A),
(2.100)
G(X(t), U(t), C),
78
где X(t) – вектор состояния;
U(t) – вектор входных переменных; Y(t) – вектор выходных переменных; A – матрица коэффициентов;
C – матрица выхода.
Если параметры системы являются постоянными по времени, то векторизованную матрицу неизвестных параметров можно представить в следующем виде:
|
|
|
|
|
dA(t) |
= 0 . |
|
(2.101) |
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
Тогда систему уравнений (2.100) можно записать следующим |
||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
dX(t) |
= F (X(t), U(t), A), |
|
|||||||||
|
|
|
||||||||||
|
dt |
|
|
|
|
|
|
|||||
dA |
= 0. |
|
|
|
|
|
|
(2.102) |
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
Нетрудно заметить, что даже если динамика объекта линейна, то |
||||||||||||
данную систему уравнений невозможно преобразовать к виду |
|
|||||||||||
|
|
dX(t) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
X |
|
|||
|
|
dt |
|
|
(2.103) |
|||||||
|
|
|
|
|
= D |
. |
||||||
|
|
dA |
|
|
|
A |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
dt |
|
|
|
|
|
|
||||
Следовательно, задача совместного оценивания параметров и состояния носит нелинейный характер относительно вектора параметров и состояния. Для решения нелинейных уравнений в общем виде существуют только итерационные методы, на основе которых и разработаны алгоритмы одновременного оценивания параметров и состояния:
–квазилинеаризация;
–метод инвариантного погружения;
–фильтры Калмана – Бьюси
1. Квазилинеаризация. Метод квазилинеаризации является итерационным методом, в основе которого лежит метод Ньютона – Рафсона.
Постановка задачи совместного оценивания параметров и состояния формулируется следующим образом:
79
Необходимо решить систему нелинейных дифференциальных уравнений
dX |
F (X(t), U(t), A) |
|
|||
|
|
|
|
||
|
dt |
|
|
|
|
|
|
|
= |
|
, |
dA |
|
|
|
||
|
|
|
|
||
|
|
||||
|
0 |
|
|
||
|
dt |
|
|
|
|
удовлетворяющих следующим граничным условиям:
Y(t) = CX(t) .
(2.104)
(2.105)
Таким образом, сформулирована многоточечная краевая задача. Метод квазилинеаризации предлагает следующий алгоритм решения данной задачи:
dX(i +1) |
= F (X(i), A(i)) + F1 (i)(X(i +1) − X(i)) + |
|
||||||||||
|
|
|
|
|||||||||
|
dt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
(2.106) |
||
+F2 (i)(A(i +1) − A(i)), |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dA(i +1) |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
при условии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CX(i +1) = Y(i +1) , |
(2.107) |
||||||||
где F1 (x), F2 (x) |
– якобианы, |
|
|
|
|
|
|
|||||
|
|
|
|
dF |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
F1 |
(i) = |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
dX |
|
|
X(i), A(i) |
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
dF |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
F2 |
(i) = |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
dA |
|
|
X(i), A(i) |
|
||||
|
|
|
|
|
|
|
||||||
При применении итерационных методов, в том числе и метода квазилинеаризации, необходимо оценить сходимость данного метода. Исследования показали, что сходимость метода гарантируется, если функция F (X, A) является выпуклой, а элементы якобианов
F1 (x), F2 (x) , стоящие над и под главной диагональю, положительны.
Оценка сходимости для звена 3-го порядка, а такие звенья являются одними и самых распространенных в реальных системах управ-
80
