книги / Численные методы решения задач строительства. Ч. 2

Одномерные элементы типа стержень, балка относятся к простейшим структурным элементам. Схематично этот КЭ изображается в виде отрезка, хотя и имеет поперечное сечение. Площадь поперечного сечения может изменяться по длине, но во многих задачах она считается постоянной. Обычно такие элементы используются при расчете стержневых систем (рам, ферм, арок, балок), в одномерных задачах распространения тепла и т.п. Уравнения, описывающие данные элементы, выводятся из теоретиче-

ских положений сопротивления материалов, т.е. из упро-

щенных механических формулировок.

Двумерные и трехмерные элементы представляют собой конечные площади или объемы сплошной среды (континуума), поэтому называются континуальными эле-

ментами.

Для построения дискретной модели двумерной области используются два основных семейства элементов: тре-

угольники и четырехугольники. Толщина элемента может быть постоянной или являться функцией координат.

Наиболее часто используемыми трехмерными элементами являются параллелепипед и тетраэдр. Уравнения, описывающие данные типы КЭ, получаются из общих соотношений механики сплошной среды и, в частности, теории упругости.

Каждый конечный элемент характеризуется определенным набором параметров, описание которых мы рассмотрим ниже.

При дискретизации расчетной схемы назначаются уз-

лы и их степени свободы.

В МКЭ следует различать глобальную (или общую) –

x, y, z (см. рис. 9.2, а) и местную – x1, y1, z1 (см. рис. 9.2, б)

системы координат. Для перехода от одной системы координат к другой используются уравнения связи между координатами в общей и местной системах координат.

61

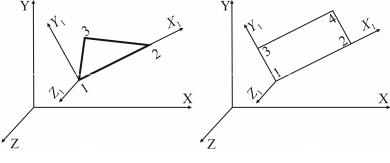
Глобальные оси координат задаются для всей конструкции и служат для описания координат узлов всей схемы, для определения направления степеней свободы, идентификации перемещений узлов. Каждому узлу и каждому КЭ присваивается порядковый номер. Обе нумерации начинаются с 1.

Местные оси координат являются атрибутом каждого КЭ и служат для задания местной нагрузки, идентификации усилий и напряжений в элементе и ориентации арматуры, используются при формулировке уравнений для КЭ. Имеет значение последовательность нумерации узлов в отдельном конечном элементе. Стержневые КЭ имеют начальный узел (н) и конечный узел (к). Местная ось x1 направлена от начала к концу (см. рис. 9.2, б).

В плоских и пространственных КЭ узлы в местной системе координат чаще всего нумеруются против часовой стрелки (рис. 9.4., а). Но в некоторых программных комплексах (например, «ЛИРА» и SCAD) это правило не соблюдается (рис. 9.4, б).

Рис. 9.4. Плоский КЭ плиты

Нумерация узлов (глобальная нумерация) – имеет существенное значение, так как именно она влияет на эффективность последующих вычислений. При нумерации узлов предпочтителен способ, обеспечивающий минималь-

62

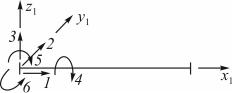
ную разность между номерами узлов в каждом отдельном элементе. Почему – об этом будет сказано ниже.

Нумерация элементов представляет собой простую процедуру. Она не влияет на вычислительные аспекты задачи, поэтому выполняется произвольно.

Искомые возможные перемещения узлов имеют как величину, так и направление, т.е. являются векторными ве-

личинами. Векторная величина представляется ее компо-

нентами, определяющими число степеней свободы неиз-

вестной скалярной величины. Их количество в каждом узле зависит прежде всего от расчетной модели.

Все реальные конструкции, здания и сооружения являются пространственными системами, но при решении конкретных задач их часто заменяют одномерными, двумерными или трехмерными расчетными моделями, это определяет размерность задачи, а соответственно, и собственную размерность конечного элемента – число степеней свободы в узле.

Так, если в качестве расчетной модели рассматривается

пространственная стержневая система, в каждом узле стержневого пространственного КЭ необходимо учитывать

шесть степеней свободы: три осевые (1, 2, 3) по направле-

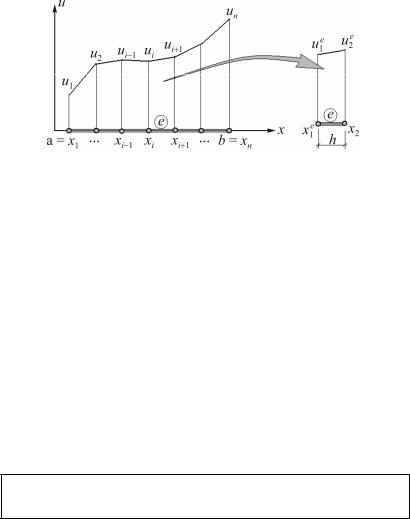
ниям x1, y1, z1 и триугловые (4, 5, 6) – повороты относительно осей x1, y1, z1 (рис. 9.5).

Рис. 9.5. Пространственный стержневой КЭ с шестью (1, 2, 3, 4, 5, 6) степенями свободы в узле [23]

63

Напряжённое состояние пространственных стержней, определяемое по результатам расчёта, описывается продольной силой в направлении оси x1, поперечными силами в направлениях осей y1, z1, изгибающими моментами относительно осей y1, z1 и крутящим моментом относительно оси x1

(см. рис. 9.5).

В строительной механике стержневых систем в основном изучаются методы расчета плоских конструкций, напряжённое состояние стержней которых, определяемое по результатам расчёта, описывается продольной силой N в направлении оси x1, поперечной силой Q в направлении оси z1, изгибающим моментом M относительно оси y1.

В каждом узле плоского стержневого КЭ (например, КЭ плоской рамы) возможны три степени свободы: две осевые – по направлениям x1, z1 и одна угловая (поворот) относительно оси y1 (рис. 9.6).

Рис. 9.6. Плоский стержневой КЭ с тремя (1, 2, 5) степенями свободы в узле [23]

В частном случае плоской шарнирно-стержневой системы (фермы), напряжённое состояние стержней которой по результатам расчёта описывается только продольной силой N, в каждом узле возможны две степени свободы: осевые перемещения по направлениям x1, z1. В пространственной шарнирно-стержневой системе в каждом узле возможны три степени свободы: осевые перемещения по направлениям x1, y1, z1.

64

Дискретизация одномерного тела (например, стержня) сводится к делению отрезка на более короткие участки

(рис. 9.7).

Рис. 9.7. Дискретизация одномерного тела (стержня)

При статическом расчете стержневых систем чаще всего каждый стержень постоянного сечения принимает-

ся за отдельный конечный элемент.

Иначе обстоит дело при динамическом расчете стержневых систем и решении задач устойчивости. Здесь обычная расчетная схема может дать очень грубый результат. Для уточнения решения стержень делят на несколько элементов.

Одномерный элемент может быть и криволинейным, но длина дуги при этом должна входить в уравнения, определяющие элементы, либо стержень должен разбиваться на большое количество прямоугольных элементов.

При разбиении двумерной области (плиты, пластины) на конечные элементы обычно используют треугольники и/или четырехугольники (рис. 9.8).

 Но при этом следует помнить, что увеличение числа узлов, а не числа элементов, повышает точность расчета.

Часто разбиение области на элементы производят в несколько этапов. Сначала область подразделяют на дос-

65

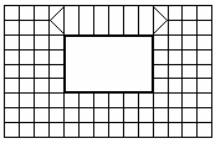
таточно крупные подобласти (подконструкции) – треугольные и четырехугольные, которые затем разбивают на более мелкие треугольные или четырехугольные элементы.

Рис. 9.8. Разбиение двумерной области на КЭ

Элементы, близкие по форме к равностороннему треугольнику, приводят к более точным результатам, чем вытянутые по форме треугольные элементы.

Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства материала. Разбиение области на элементы обычно начинают от ее границы с целью наиболее точной аппроксимации формы границы. Если границы области криволинейные, то криволинейные границы элементов чаще всего заменяются прямыми отрезками. Затем производится разбиение внутренних областей.

При разбиении трехмерного тела (массивного тела) трудно наглядно представить расположение элементов в дискретной модели. Поэтому более желательными для трехмерных моделей являются четырехгранные элементы (параллелепипеды).

Равномерное разбиение, когда все элементы имеют одинаковые форму и размеры, применяется крайне редко,

потому что существуют концентрация напряжений, тем-

66

пературные градиенты и т.п., где проводится более мелкая разбивка на конечные элементы.

Резкого изменения размеров конечных элементов на границах подобластей стараются избегать. Возможность варьировать размеры элементов – важное достоинство МКЭ. При этом приходится сталкиваться с довольно деликатной ситуацией. С одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получались приемлемые результаты, а с другой стороны, применение крупных элементов сокращает вычислительную работу.

Нужно иметь некоторые общие соображения об окончательных значениях искомых параметров для того, чтобы можно было уменьшить размеры элементов в тех областях, где ожидаемый результат может очень сильно меняться

(большие градиенты усилий, напряжений), и увеличить их там, где ожидаемый результат почти постоянен. Плохое или несовершенное разбиение будет приводить к ошибочным результатам, если даже остальные этапы метода будут осуществляться с достаточной точностью. Навыки в дискретизации области обычно приходятс опытом.

Вблизи особых точек, таких где имеется резкая концентрация напряжений (места стыков, приложения сосредоточенных нагрузок и т.п.), применение конечных элементов (равно как и других методов дискретизации) обычно затруднено, особенно в представлении поля напряжений. Приходится резко сгущать сетку конечных элементов и существенно увеличивать размер задачи. Однако это сгущение сетки может и не привести к результату. Это подталкивает к дополнительному анализу ситуации и уточнению

расчетной схемы [16].

В современных профессиональных конечно-элементных программных комплексах разбивка на конечные элементы чаще всего производится автоматически, но учесть все осо-

67

бенности работы конструкции при создании расчетной моделиконструкциидолжен исследователь.

9.2.2. Определение аппроксимирующих функций элемента

Расчетная модель конструкции состоит из двух частей: расчетной схемы и набора аппроксимирующих функций.

Расчленение расчетной области на КЭ дает возможность рассматривать отдельные конечные элементы не только для практического решения задачи, но и для теоретического исследования аппроксимирующих функций, абстрагируясь при этом от геометрии конструкции, граничных условий, нагрузки.

Определение аппроксимирующих функций элемента можно выполнить один раз для типичного элемента области, безотносительно к его топологическому положению в ней. Полученная функция используется далее для всех остальных элементов области того же вида. Эта особенность является важным аспектом МКЭ. Благодаря ей элементы с однажды определенными функциями легко включаются в библиотеку элементов соответствующих программных комплексов. Далее эти элементы применяются для решения разнообразных краевых задач

Аппроксимирующие функции – это непрерывные функции, определяемые в каждой конкретной задаче (перемещение, температура и т.п.), соответствующие степеням свободы. В задачах статического расчета конструкций аппроксимирующие функции описывают перемещения (линейные и угловые).

В качестве аппроксимирующих функций элементов чаще всего используются полиномы, которые подбираются так, чтобы обеспечить непрерывность искомой функции в узлах на границах элементов. На выбор вида этих функций

68

влияет множество факторов, а именно: размерность задачи (1D – одномерная, 2D – двумерная, 3D – трехмерная), гео-

метрическая форма элемента, число узлов в элементе.

Непрерывную функцию (е) в произвольной точке е-го конечного элемента обычно аппроксимируют полиномом

ваемой точке.

Далее задача заключается в определении неизвестного вектора A(е) и свободного члена А0. Для этого, используя условие непрерывности функции в узлах, коэффициенты полинома выражают через вектор узловых значений

функции (е) (неизвестные в МКЭ) и координаты узлов, в результате чего получают аппроксимирующую функцию в виде

где N(е) – матрица, элементы которой в специальной литературе по методу конечных элементов [3, 15] называют функциями формы конечного элемента.

Функции формы в каждой точке конечного элемента можно вычислить через координаты самой точки и координаты узлов элемента.

Одномерные, двумерные и трехмерные КЭ называют

линейными, квадратичными или кубическими, в зависимо-

сти от степени интерполяционного полинома, используе-

мого в качестве аппроксимирующей функции элемента.

Квадратичные и кубические КЭ отличаются от линей-

ных КЭ тем, что кроме граничных узлов имеются дополнительные внутренние узлы, один и два соответственно. До-

69

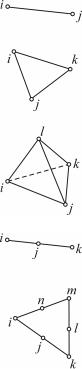
бавление узлов в середину сторон элементов повышает точность расчета и дает возможность моделирования криволинейных границ (рис. 9.9).

Рис. 9.9. Примеры интерполяционных полиномов

Чаще всего в расчетах строительных конструкций используют линейные КЭ. Полиномы линейных КЭ содержат константы и линейные члены. Число коэффициентов в таком полиноме на единицу больше размерности координатного пространства. Некоторые примеры интерполяционных полиномов приведенына рис. 9.9.

70