книги / Численные методы решения задач строительства. Ч. 2

Аппроксимирующая функция должна быть согласована с соответствующим элементом таким образом, чтобы ее

коэффициенты i определялись однозначно.

 Определить аппроксимирующую функцию элемента – это значит найти ее коэффициенты.

Определение коэффициентов интерполяционного полинома рассмотрим на примере одномерного линейного элемента.

Одномерный линейный элемент представляет собой отрезок, изображенный на рис. 9.10. По длине отрезка зна-

чение функции аппроксимируем полиномом

будем считать, что узловые значения искомой непрерывной функции, определенные на концах отрезка, известны.

Обозначив узлы индексами i и j, а узловые значения искомой функции i и j соответственно, коэффициенты 1

и 2 можно определить в соответствии с условием непрерывности функции в узлах:

71

решение которой дает

Линейные функции, которые заключены в скобки (функции формы), зависят только от координат узлов х, в МКЭ обычно обозначаются буквой N.

Выражение (9.13), можно записать в матричном виде:

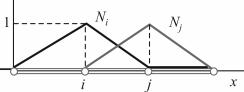
Функции формы обладают следующим свойством: функция Ni равна 1 в узле с номером i и равна 0 в j-м узле. Аналогично функция Nj равна 0 в i-м узле и равна 1 в узле с номером j. Графически это представлено на рис. 9.11.

Описанная процедура определения коэффициентов аппроксимирующих функций может быть обобщена и на двумерные и трехмерные элементы. При этом следует понимать, что, так же как и в случае одномерного элемента:

72

1)функция формы Ni равна 1 в узле с номером i и нулю в узлах j и k и др. То же относится и к другим узлам и функциям формы;

2)функция изменяется линейно между двумя любыми узлами. Поэтому, чтобы аппроксимировать быстро ме-

няющуюся функцию , необходимо использовать очень малые по величине элементы;

3) если провести любую прямую линию, пересекающую две стороны элемента, то вдоль этой линии значение

будет постоянно.

Рис. 9.11. Функции формы

Заметим, что функции формы для одномерного линейного элемента были получены безотносительно его поло-

жения в области и физического смысла решаемой задачи. Поэтому они удовлетворяют всем элементам данного типа.

Рассмотренные выше интерполяционные формулы были

получены для скалярной величины . Но векторная величи-

на (перемещение) имеет как величину, так и направление

и представляется ее компонентами, количество которых определяется числом степеней свободы в каждом узле, которые рассматриваются как неизвестные скалярной величины.

Можно показать, что функции формы (9.15) представ-

ляют собой полиномы Лагранжа [3, 8]

73

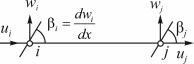
и могут быть получены непосредственным использовани-

ем интерполяционной формулы Лагранжа. Отсюда и на-

звание элементов, в которых в качестве узловых параметров используются только значения функции в узлах – ла-

гранжевы элементы.

Для решения некоторых задач, например при расчете изгибаемых элементов (рам, балок, плит перекрытий), в качестве узловых параметров функции целесообразно использовать не только значения самой функции, но и зна-

чения ее производных.

В этом случае в качестве аппроксимирующих полиномов вместо полиномов Лагранжа используют полиномы Эрмита. А элементы, в которых их используют, называются соответственно эрмитовы элементы.

Для иллюстрации на рис. 9.12 показан одномерный изгибаемый элемент балки или рамы с двумя узлами i и j, имеющий по три степени свободы в каждом узле:

прогиб w, угол поворота dwdx и перемещение вдоль элемента u.

Рис. 9.12. Одномерный изгибаемый КЭ

9.2.3. Получение разрешающих уравнений МКЭ

Процесс получения разрешающих уравнений МКЭ рассмотрим на примерах плоской стержневой системы (рис. 9.13) и плоской задачи теории упругости.

74

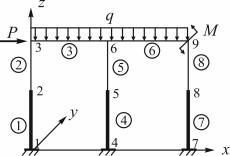
Плоская стержневая система

Рис. 9.13. Плоская стержневая система

Задачу будем решать в перемещениях. Перемещения стержня, работающего на изгиб, полностью определяется из решения системы дифференциальных уравнений

дополнив которую краевыми условиями, получим краевую задачу.

Здесь u – перемещения вдоль оси стержня; w – перемещения перпендикулярно оси стержня.

Данная краевая задача заменяется вариационной задачей, в которой функционал – потенциальная энергия системы имеет вид

75

Для конструкции, разбитой на конечные элементы, функционал (9.17) записывается в виде суммы элементных интегралов, т.е. суммы интегралов такого же вида, составленных для каждого элемента:

(9.18)

s f (x)w f1 (x)u ds.

0

Как и в методе Ритца, решение будем искать в виде линейной комбинации некоторых функций, но для каждого конечного элемента:

i

где i – неизвестные коэффициенты (как в методе Ритца –

(e)

неизвестные параметры); i (x) – координатные функции

элемента, которые в данном случае выбираются так, чтобы при подстановке координат соответствующих узлов в (9.19)

коэффициенты i равнялись бы перемещениям узлов конечных элементов, т.е. вектор

определяет перемещения вдоль оси и перпендикулярно оси стержня внутренних точек каждого элемента.

Вид функций i и i зависит от типа конечного элемента. Для изгибаемой (рамной) конструкции обычно

76

применяются эрмитовы КЭ, и координатные функции выбираются в виде линейного и кубического полиномов:

Это связано с тем, что порядок полинома, зависящий от числа используемых в каждом узле элемента данных о непрерывной функции, должен быть не ниже наивысшего порядка производной, входящей в функционал – потенциальную энергию системы (9.2).

В матричной форме решение (9.9) после определения коэффициентов интерполяционных полиномов можно записатькак

Здесь N(x) – функции формы. Они зависят только от координат и размеров элементов. Их число равно числу узлов сет-

ки; вектор – искомые перемещения узлов конечных эле-

ментов состоит из N n-мерных векторов (n – число степеней свободывузле, вданном случае– 3; N – число узлов).

Подставляя (9.19) в (9.18) с учетом (9.20)–(9.22) и произ-

водя интегрирование, получаем вместо функционала функ-

цию П, зависящую отузловыхзначений параметров i.

Для нахождения экстремума этой функции, а соответственно, и функционала дифференцируем Ппо параметрам i.

77

В результате получаем систему линейных алгебраических уравнений относительно узловых значений искомой функции, которая представляет собой разрешающие уравнения МКЭ и в матричном виде может быть записана как

Здесь К – матрица жесткости (квадратная, симмет-

ричная, ленточной структуры размером [m m], где m = N n; – вектор узловых значений искомой функции (пере-

мещения узлов); F – вектор внешней нагрузки.

Плоская задача теории упругости

Аналогично решается плоская задача теории упруго-

сти, к которой можно отнести расчет напряженнодеформированного состояния таких строительных конструкций, как плиты перекрытий и покрытий, стеновые панели, протяженные плотины, ленточные фундаменты и т.д. Все эти конструкции могут быть представлены в виде двумерного плоского тела – пластины. Пластина – термин, используемый в строительной механике для описания расчетной схемы конструкции, один из размеров которой (толщина h) значительно отличается от двух других.

Исторически именно при решении плоской задачи теории упругости впервые были использованы идеи метода конечных элементов в их явном виде. Здесь МКЭ раскрывает все свои возможности и позволяет рассматривать конструкции сложной формы.

Пусть область с границей S разбита на конечные эле-

менты (e) – треугольные или/и четырехугольные (рис. 9.14).

78

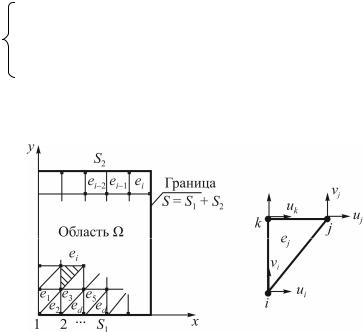
Получаемое решение будет относиться к области, состоящей из совокупности конечных элементов е1, е2,…, еk.

Краевая задача

заменяется вариационной задачей. Краевые условия при этом могут быть и другими.

Рис. 9.14. Разбиение области на конечные элементы

Функционал – потенциальная энергия системы в

данной задаче имеет вид

Решение в виде линейной комбинации функций ищем для каждого конечного элемента:

i

79

вертикальное перемещения точки внутри элемента; i –

(e)

неизвестные коэффициенты; i (x) – координатные

функции элемента, которые выбираются так, чтобы при подстановке координат соответствующих узлов в (9.28)

коэффициенты i равнялись бы перемещениям узлов конечных элементов.

В матричной форме решение(9.28) можно записатькак

где N(x) – функции формы. Они зависят только от коор-

динат и размеров элементов.

Нижние индексы обозначают размерность матрицы; n определяет размерность задачи (n = 1 – одномерная, n = 2 – плоская, n = 3 – пространственная), а m обычно предполагается кратным n (m = Nn), N – число узлов конечного элемента. В частности, для плоской задачи m = 2N.

Вектор – искомые значения перемещений узлов конечных элементов – состоит из N n-мерных векторов.

Минимизация функционала (9.27) осуществляется на множестве узловых значений искомой функции . При

этом функционал (9.27) записывается в виде суммы интегралов по элементам:

80