
книги / Численные методы решения задач строительства. Ч. 2
.pdfE |
1 |
|
|
u 2 |
|
u 2 |
|
. (9.30) |
П |
|
|
|
|
|
|
2 f (x, y)u |
|
e 1 |
2 |
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
Представление интеграла по области в виде суммы интегралов, каждый из которых вычисляется по отдельному элементу, позволяет рассматривать различные свойства материалов для различных элементов. Это является важным свойством МКЭ.
Подставляя (9.28) в (9.30) и производя интегрирование, получаем вместо функционала функцию П, зависящую от узловых значений перемещений.
Для нахождения экстремума этой функции, а соответственно, и функционала (9.27) дифференцируем функцию П
по параметрам u(i) и v(i) вектора (i = 1, 2, …, N) и при-
равниваем к нулю. В результате получаем разрешающую систему m (или 2N – для данной задачи) уравнений относительно неизвестных узловых параметров, которую в матричной форме также можно записать в виде (9.24).
Перемещения в любой точке каждого конечного эле-
мента в дальнейшем могут быть определены по формуле (9.28). Зная перемещения во всех точках элемента, можно
определить относительные деформации и напряженияв каждой точке конструкции, которые зависят от вида на- пряженно-деформированногосостояния(см. подразд. 9.2.5).
9.2.4. Решение системы линейных алгебраических уравнений
Система линейных алгебраических уравнений
К F , полученная в процессе минимизации функ-
ционала, обладает положительно определенной симметричной матрицей ленточной структуры, матрица коэф-
81
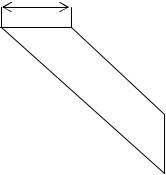
фициентов которой получается сильно разреженной (рис. 9.15). Это связано с тем, что каждый из элементов связан с ограниченным количеством соседних КЭ.
Количество уравнений разрешающей системы nур за-
висит от количества узлов nузл |
и числа степеней свободы |
||||||||
в узле Q и вычисляется по формуле |
|
|
|
|
|||||
|
|
nур nузл Q. |
|
|
|
(9.31) |
|||
Ширина ленты |
|
|
|
|
|
||||
с |
с |
0 |
с |
0 |
0 |
0 |
0 |
||
|
с |
с |
с |
с |
с |
0 |
0 |
0 |
|
|
0 |
с |
с |
0 |
с |
с |
0 |
0 |
|
|
|
||||||||
|
с с 0 с с с |
с 0 |
|
||||||
К |
|
||||||||
|
0 |
с |
с |
с |
с |
с |
с |
с |
|
|
0 |
0 |
с |
с |
с |
с |
с |
с |
|
|
|
||||||||
|
0 |
0 |
0 |
с |
с |
с |
с |
с |
|
|
0 |
0 |
0 |
0 |
с |
с |
с |
с |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 9.15. Матрица жесткости ленточной структуры
Ширина ленты зависит от числа степеней свободы узлов и способа нумерации последних. Под числом степеней свободы понимают количество неизвестных пара-
метров, определяемых в каждом узле.
Например, произвольная пространственная конст-
рукция в каждом узле имеет шесть степеней свободы (три линейных перемещения и три угловых). При расчете пло-
ской стержневой системы (рамы, балки) в каждом узле определяют три неизвестных (два линейных перемещения и угол поворота), т.е. число степеней свободы в узле такой конструкции равно трем. Плоская ферма или балка-стенка
82
вкаждом узле имеет две степени свободы (перемещения вдоль осей Х и У), а пространственная ферма – три (пе-
ремещения вдоль осей Х, У и Z).
При нумерации узлов предпочтителен способ, обеспе-
чивающий минимальную разность между номерами узлов
вкаждом отдельном элементе. Если максимальную раз-
ность между номерами узлов для отдельного конечного элемента обозначить R , то ширина ленты L вычисляется по формуле
L (R 1)Q. |
(9.32) |
Чем меньше ширина ленты L, тем меньший объем ОП требуется для хранения матрицы при реализации МКЭ на ЭВМ и тем меньше затраты машинного времени на решение разрешающей системы уравнений.
В некоторых случаях уменьшение числа L может быть достигнуто последовательной нумерацией узлов при дви-
жении в направлении наименьшего размера рассматриваемой области.
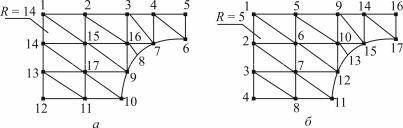
На рис. 9.16 приведены два различных способа нумерации узлов произвольной области, разбитой на конечные элементы.
Рис. 9.16. Варианты нумерации узлов: (а) R = 14; ширина ленты при двух степенях свободы в узле получается равной 30, а при трех степенях свободы 45; (б) R = 5; ширина ленты при двух степенях свободывузлеравна12, апритрех степенях свободы18
83
Рациональная нумерация во втором случае по сравнению с первым сокращает необходимый объем оперативной памяти почти в три раза.
Для численного решения разрешающей системы уравнений обычно используют методы блочного исключения
Гаусса, Холецкого, LDLT-факторизации и др. [8, 10, 3].
А для уточнения полученного решения – итерацион-
ные методы.
9.2.5.Основные соотношения теории упругости
вметоде конечных элементов
Воснове курса теории упругости [1, 15] лежат три группы определяющих уравнений:
–закон равновесия в форме дифференциальных соотношений частных производных внутренних напряжений;
–линейные геометрические соотношения связи между перемещениями и деформациями, выражающие непрерывность и относительную малость перемещений, которые называют еще геометрическими уравнениями Коши;
–линейные физические уравнения (закон Гука) связи между напряжениями и относительными деформациями.
Кроме того, полученные решения должны удовлетворять уравнениям совместности Сен-Венана, выраженным через относительные деформации или напряжения.
ВМКЭ, в отличие от теории упругости, статическое равновесие представлено уравнениями метода перемещений, выражающими равновесие узлов.
Определив перемещения узлов конечных элементов из разрешающей системы линейных алгебраических уравне-
ний (9.24), можно найти относительные деформации ,
используя соотношения связи. Для плоской задачи связь между деформациями и перемещениями в конеч-
ном элементе имеет вид
84
x |
u |
, |
y |
v |
, |
xy |
u |
|
v . |
|
x |
|
|
y |
|
|
y |
|
x |
Запишем эти равенства в матричной форме:
В .
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
||||||
|
x |
|
u |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
, В |
|
|
|
|
|||
Здесь |
y |
|
, |
|
0 |
|
|
|
. |
||
|
|
|
|||||||||
|
|
|
v |
|
|
|
|
|
y |
||
xy |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||
|
|
|
|
|
|
|
|
x |
|||
(9.33)
(9.34)
Матрица [B] получается дифференцированием матрицы функций формы [N]. Фактические значения коэффици-
ентов матрицы [B] зависят от типа используемого элемента и от вида рассматриваемой задачи.
Линейные физические уравнения (закон Гука) связи между напряжениями и относительными деформациями в матричной форме для плоской задачи можно записать как:
C , |
(9.35) |
х
где у – вектор напряжений; [С] – матрица упру-
ху
гой податливости содержит упругие константы материала и зависит от вида напряженно-деформированного состоя-
ния (НДС) конструкции.
Пользователи программ, реализующих МКЭ, должны отчётливо понимать различие между двумя версиями пло-
ской задачи (рис. 9.17): плоским напряжённым состоянием (ПНС) и плоским деформированным состоянием (ПДС).
85
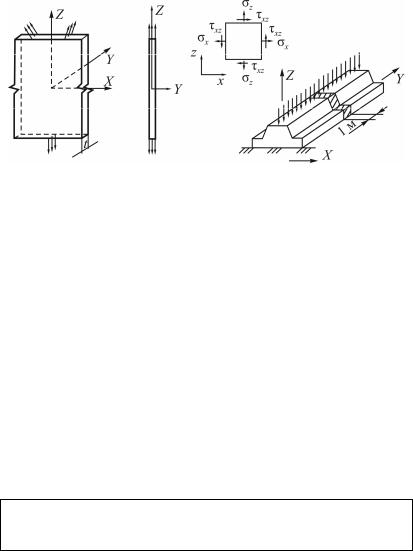
а |
б |
Рис. 9.17. Различие между двумя версиями плоской задачи: плоское напряжённое состояние(а) и плоская деформация(б) [23]
Плоское напряжённое состояние
Плоское напряжённое состояние (рис. 9.17, а) реализуется в тонких пластинах и относится к расчётным схемам, которые располагаются на плоскости вместе с системой действующих нагрузок. Примером таких объектов могут служить изгибаемые высокие балки, балки-стенки. В программных комплексах «ЛИРА» и SCAD эти конструкции обычно располагают вертикально в плоскости x0z.
Принимая срединную плоскость за плоскость x0z, на плоскостях при y t 2 имеем y 0 , xy yя 0 , а пе-
2 имеем y 0 , xy yя 0 , а пе-
ремещения и относительные деформации, перпедикулярные к плоскости действия сил, не равны нулю.
Следует отметить, что тонкие пластины при действии внешних нагрузок, параллельных срединной поверхности, могут терять местную устойчивость.
Плоское деформированное состояние
Плоское деформированное состояние (рис. 9.17, б) относится к расчётным схемам протяжённых сооружений типа ленточных фундаментов, насыпей, откосов, подпорных
86
стенок, сохраняющих свои поперечные размеры, а также систему действующих сил на некотором протяжении.
Для расчёта напряжённого состояния сечений выделяется отрезок единичной ширины (1 м, 1 см). Расчётная область обычно помещается на плоскости x0z. В отличие от предыдущего варианта плоской задачи, здесь относительные деформации εy на боковых гранях равны нулю, а нормальные к плоскостидействиясил εz нулевыминеявляются.
При идеализации плоских сплошных тел прилегающие друг к другу КЭ считаются шарнирно скреплёнными в узлах. Поэтому в узлах расчётных областей, напряжённодеформированное состояние которых соответствует плоскому напряжённому состоянию или плоской деформации, приняты степени свободы по направлениям осей X и Z. Результатом расчёта таких систем являются нормальные σx, σz и касательные τxz компоненты напряжений (см. рис. 9.17).
Уравнения связи между напряжениями и относительными деформациями в МКЭ описываются формулами обобщённого закона Гука и в прямоугольных координатах для сплошных изотропных расчётных областей имеют следующий вид:
для плоского напряжённого состояния
|
x |
1 |
x z , |
|
z |
1 |
z x , |
|
|||||
|
E |
E |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
, |
(9.36) |
||
|
|
|
|
|
xz |
2 xz (1 ) |
|
|
|||||
|
|
|
|
xz |
; |
|
|
||||||
|
|
|
|
|
G |
|
E |
|
|
|
|
|
|
для плоской деформации |
|
|
|
|
|
||||||||
x |
1 |
x 1 z |
, z 1 |
|
z 1 |
|
x , |
||||||
|
E |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
xz |
xz |
|
2 xz 1 |
. |
|
(9.37) |
|||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
G |
|
E |
|
|
|
|
|
|
87

Здесь E – модуль упругости; – коэффициент Пуассона
(поперечной деформации); G |
E |
– модуль сдвига. |
2 1 |
В МКЭ уравнения закона Гука (9.35) обычно используются в обратной записи: напряжения определяются в за-
висимости от деформаций. |
|
D . |
(9.38) |
Матрица упругости [D] в данном случае для ПНС имеет вид
|
|
|
Е |
1 |
|
0 |
|
|
|
||
D |
|
|
|
1 |
0 |
|
; |
(9.39) |
|||
1 |
2 |
||||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
0 |
(1 ) |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
в случае плоской деформации (ПДС)
D |
|
|
Е(1 ) |
|
|
|
|
|
(1 |
)(1 2 ) |
|
|
|
||||
|
|
|
|
|
|
|||
|
|
1 |
(1 ) |
0 |
|
(9.40) |
||
|
(1 ) |
1 |
|
0 |
|
|
||
|
|
. |
|
|||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
(1 2 ) 2(1 ) |
|
|||
9.2.6. О расчете изгибаемых плит
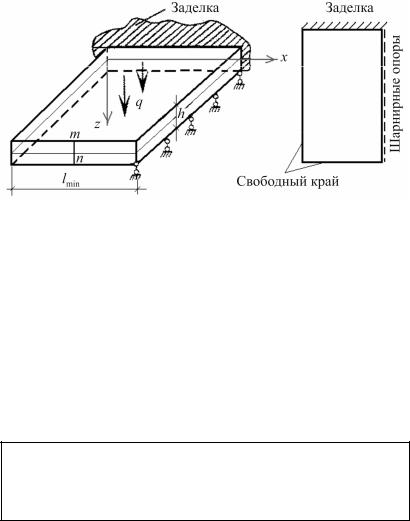
Пластина, нагруженная перпендикулярно её плоскости и работающая преимущественно на изгиб из собственной плоскости, называется плитой (рис. 9.18).
Пластина может быть самостоятельной конструкцией или входить в состав пластинчатой системы.
Горизонтальные и вертикальные пластинки, соединенные между собой связями, образуют несущую систему,
88
которую применительно к зданиям называют стеновой системой. Наклонно расположенные пластинки могут образовывать пролетные несущие конструкции.
Рис. 9.18. Расчетная схема плиты и условия опирания на плане
Плоскость, которая делит толщину пластины пополам, называется срединной плоскостью плиты. При нагружении плита изгибается, и ее срединная плоскость превращается в поверхность. Перемещения точек срединной плоскости вдольосиz называютсяпрогибамии обозначаютсячерезw.
Считается, что толщина плиты h должна быть намного меньше ее характерного размера в плане lmin. Но это понятие не вполне определено. Все зависит от соотношения
h |
и от жесткости плиты. |
|
l |
||
|
||
min |
|
Плита считается тонкой, если ее толщина меньше других размеров не менее чем в 5 раз. Тонкая плита, у которой максимальный прогиб под действием поперечной нагрузки не превышает четверть её толщины, называется жесткой.
При расчете тонких жестких плит обычно используются три допущения.
89
1.Принимается, что прямолинейные элементы, нормальные к срединной плоскости, остаются после деформации прямыми, нормальными к деформированной средин-
ной поверхности (гипотеза прямых нормалей). Или, дру-
гими словами, отрезок mn (см. рис. 9.18), проведенный перпендикулярно срединной плоскости, при изгибе не искривляется, он остается прямым и нормальным к срединной поверхности.
2.Считается, что пластина не сжимаема по толщине или слои, параллельные срединной поверхности, не давят
друг на друга, т.е. напряжениями z пренебрегают.
3. Срединная поверхность при изгибе не деформируется в своей плоскости при z = 0, т.е. деформацииx , y , xy при z = 0 отсутствуют.
Эти допущения позволяют выразить перемещения всех точек плиты через поперечные перемещения срединной плоскости. Расчет пластин с использованием этих допуще-
нийсоставляетоснову технической теорииизгиба плит.
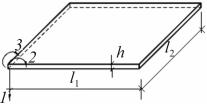
Этим гипотезам соответствует простейшая модель изгибаемой плиты. На практике при реализации этой модели МКЭ используются КЭ с тремя степенями свободы в каждом узле: вертикальным перемещением по направлению Z (1) и двумяугловымиотносительно осей X (2) иY (3) (рис. 9.19).
Рис. 9.19. Четырёхугольный изгибаемый КЭ с тремя степенями свободы в узле
90
