книги / Математическое моделирование дискретные подходы и численные методы

Уравнения такого же вида могут быть получены для температуры – уравнения теплопроводности.

При решении краевых задач МСС, то есть систем записанных выше балансовых уравнений с использованием линейных определяющих соотношений, получаемых в результате применения принципа Онзагера, необходимо задавать начальные и граничные условия на входящие в уравнения полевые величины. Для механических характеристик вводят два типа граничных условий – условия нагружения или статические граничные условия

и условия «закрепления» или кинематические граничные условия на вектор перемещений или скорости:

Эти условия могут рассматриваться как частный случай условий на поверхностях разрыва в сплошных средах, подробный вывод которых можно найти в [4–5, 11–12].

При решении задачи диффузии или теплопроводности граничные условия могут быть заданы несколькими способами. В теории диффузии различают граничные условия 1-, 2-, 3- и 4-го родов (граничные условия 4-го рода также называют условиями сопряжения). В зависимости от задачи может оказаться, что число граничных условий превышает число реальных границ. Например, в задаче для сферических или цилиндрических тел необходимо задать условия как на внешней поверхности (границе), так и в центре, где исследуемые поля не должны принимать бесконечных значений. Часто граничные условия задаются «на бесконечности».

61

1. Граничные условия 1-го рода

В граничных условиях 1-го рода задается распределение концентрации диффундирующего вещества по поверхности S тела, как функция координат и времени.

В частном случае концентрация на поверхности является функцией только времени:

c S = cs (t) .

Вболее простом случае концентрация на поверхности может быть постоянной (условие Дирихле).

2. Граничные условия 2-го рода

Вусловиях 2-го рода задается распределение плотности потока концентрации примеси для каждой точки поверхности:

Если поток на поверхности зависит от координаты, но не зависит от времени, граничное условие называется условием Неймана. Важным частным случаем является отражающая стенка (отсутствие потока через внешние поверхности образца – условие диффузионной изоляции):

Jc S = 0 .

Впоследнем случае граничная поверхность изолирована (диффузия через нее невозможна, поток диффундирующего вещества через границу равен нулю).

3. Граничные условия 3-го рода

Вграничных условиях 3-го рода задают закон конвективного массообмена между поверхностью тела и окружающей средой:

где c0 (t) – концентрация вещества в окружающей среде. Это условие подразумевает, что концентрация не мгновенно устанавливается на поверхно-

62

сти, а в процессе некоторого времени, то есть граница оказывает сопротивление диффузионному потоку (иногда более сильное, чем собственно диффузия). В этом случае поток не является постоянным, а изменяется как разность между концентрациями в твердом теле и в окружающем объеме.

Заметим, что на практике часто встречаются однородные граничные условия, когда правые части (1.124)–(1.127) равны нулю.

4. Граничные условия 4-го рода

Граничные условия сопряжения (условия 4-го рода) соответствуют массообмену поверхности тела с окружающей средой или массообмену соприкасающихся твердых тел, когда концентрации на соприкасающихся поверхностях одинаковы:

в соприкасающихся средах. Первое равенство выражает условие непрерывности концентрационного поля, а второе – закон сохранения энергии на поверхности соприкосновения двух сред – потоки на границе должны быть равны друг другу. В отличие от теплопроводности, где разрыва температуры на границе раздела фаз нет, в процессах диффузии на границе раздела твердых тел возможны разрывы концентраций. Лишь в частном случае, при равенстве коэффициентов растворимости в обеих фазах, разрыва в концентрационном поле на границе фаз нет.

Начальные условия. Задание начального условия для уравнения диффузиизаключается втом, чтодля некоторого момента времени t = t0 (обычно

При решении эллиптического уравнения диффузии дополнительно необходимозадаватьначальныеусловиянаскоростьизмененияконцентрации:

Причем начальные условия (1.130)–(1.131) должны быть согласованы с краевыми условиями.

63

При решении диффузионных уравнений обычно выделяют три вида тел: неограниченно простирающаяся от источника во все стороны среда (бесконечное тело), простирающаяся в одном направлении среда (полубесконечное тело) – в этом случае в удаленных точках концентрация равна нулю в ходе всего диффузионного процесса, и ограниченная по всем направлениям среда (в конечном итоге вещество занимает все пространство). В последнем случае решение уравнения диффузии зависит от геометрии среды – пластина, цилиндр, шар, куб, призма и другие.

Возможны предельные случаи, когда можно пренебречь начальными условиями. Так, для конечных тел произвольной формы начальные условия оказывают влияние на процесс распределения примеси лишь на начальной стадии нестационарной диффузии: начиная с некоторого момента t* наступает такой режим диффузии, при котором распределение концентрации в теле определяется только граничными условиями и не зависит от начальных. Дифференциальное уравнение диффузии вместе с заданными дополнительными условиями полностью определяет краевую задачу диффузии, подлежащую решению.

Вопросы для самопроверки

1. Как называются записанные соотношения, и какие из них справедливы для любых сред?

2. Пусть движение плоской сплошной среды описывается законом следующего вида: x1 = 2 X 1 − X 2 , x2 = X 1 − 2 X 2 , где xi – координаты точек среды в текущей конфигурации Kt, а X i – в отсчетной конфигурации K0. Имеет ли такое движение физический смысл?

3.Можно ли независимо задавать вид функции внутренней энергии среды и химический потенциал?

4.Чему равна сумма концентраций всех компонент смеси?

5.Можетлиполноеизменениеэнтропиисистемыбытьотрицательным?

6.Как определяется кинетическая энергия смеси компонент?

7.Для каких случаев справедливо уравнение диффузии эллиптического типа?

64

1.4. ПРАКТИЧЕСКОЕ ВВЕДЕНИЕ В ПАКЕТ «MATHEMATICA»

При разработке и исследовании математических моделей различной сложности требуется использование знаний тех или иных разделов математики, применение соответствующих подходов и методов решения задач. В настоящее время существует масса специализированных программных комплексов, позволяющих довольно эффективно применять самые разные математические методы для решения возникающих при выполнении научных исследований проблем. Разумеется, никакой пакет программ никогда не сможет дать готовое решение задачи, представляющей научную ценность. Он является лишь инструментом в руках исследователя, упрощающим проведение некоторых промежуточных этапов, выполнение математических выкладок и позволяющим концентрировать внимание на принципиально важных вопросах об установлении причинно-следственных связей в исследуемых процессах, выяснении и проверке механизмов анализируемых явлений и в конечном счете их формализации на языке математики. В качестве примера такого инструмента выбран пакет «Mathematica» производителя Wolfram Research, наиболее приспособленного, по мнению авторов, к выполнению научных исследований. От версии к версии этого пакета синтаксис применения некоторых функций и значения опций, используемых во встроенных функциях, несколько меняется. Изложение данного раздела ориентировано на версию 7.0.

Задача использования Пакет «Mathematica» предоставляет среду для одновременной отладки алгоритмов, используемых при построении дискретных и непрерывных математических моделей, графического представления и обработки результатов их работы, быстрого выполнения необходимых аналитических преобразований, численного исследования упрощенных вариантов дискретных и континуальных моделей. Подчеркнем, что с вычислительной точки зрения использование пакета «Mathematica» неоправданно, поскольку узкоспециализированная программа, написанная для численной реализации приближенных методов МСС молекулярной динамики или статики, метода клеточных автоматов и других дискретных подходов к моделированию физико-механических процессов, будет выполнять расчеты для больших систем дискретных объектов несоизмеримо быстрее. Особенно это будет заметно при использовании в программировании технологий многопроцессорных вычислений.

Пакет «Mathematica» может использоваться на разных уровнях сложности решаемых задач или владения пакетом. Его можно применять как:

65

–простой калькулятор: выполнять арифметические действия, находить приближенные и точные значения математических функций и выражений, строить графики функций;

–развитый калькулятор: выполнять логические операции, работать с комплексными числами, производить символьные преобразования выражений, выполнять действия математического анализа (нахождение пределов последовательностей и функций, дифференцирования, интегрирования, разложение функций в ряды) как в точном символьном представлении, так и численно, работать с векторами и тензорами разного ранга, задавать собственные функции, аппроксимировать табличные числовые данные функциональными зависимостями, использовать более сложную графику для анализа математических соотношений;

–язык программирования: составлять программы на базе специальных конструкций – списков, использовать методы функционального программирования, применять процедурное программирование, элементы объектно-ориентированного программирования;

–инструмент научно-исследовательской работы (НИР): использо-

вать все описанные выше возможности пакета, а также получать аналитические и численные решения уравнений от алгебраических до дифференциальных уравнений, как обыкновенных, так и в частных производных, решать краевые задачи с граничными условиями разного рода, работать со специальными математическими функциями, использовать специализированные способы обработки (включая набор методов математической статистики и вейвлет-анализ) и представления данных, в том числе получаемых в пакете «Mathematica» решений краевых задач.

Первое знакомство. При описании работы с пакетом будем придерживаться приведенной схемы перехода от использования его простейших возможностей ко все более сложным, не указывая впрочем, границ между указанными уровнями. Начнем с основных приемов, необходимых для работы в пакете «Mathematica 7.0». После запуска программы на экране появляется основное окно, в котором и происходит вся работа – «рабочая тетрадь» (notebook). При соответствующих настройках пакета появляется

идополнительное окно, служащее для упрощения ввода некоторых специальных символов (греческих букв, интегралов, матриц и так далее) – «палитра». Также горизонтальное окно-полоска в верхней части экрана с кнопками пунктов меню. Из этих пунктов упомянем сохранение и за-

грузку файлов с результатами своей работы в пакете: кнопки «File» → «Save» или «Save as» (сохранение) и «File» → «Open» (открытие) файла.

66

Для вызова окна палитры используется кнопка «Palettes», после нажатия на которую в появившемся окне надо выбирать раздел «Other», а в нем – «Basic Math Input». Другая кнопка, которую нужно регулярно использовать, – это кнопка «Help», позволяющая получить справку по многим вопросам о работе в пакете. В частности, рекомендуется познакомиться с «Help» → «Virtual Book». В дальнейшем интерфейс пакета и содержимое меню обсуждаться практически не будут. Любой пользователь персонального компьютера с начальным опытом может разобраться в них самостоятельно. Более подробную информацию о работе в пакете можно найти, например, в [3] или воспользоваться встроенной книгой помощи.

При вводе любого символа в рабочем окне открывается так называемая ячейка (отмечена квадратной скобкой по правому краю рабочего окна), в котором и появляются вводимые символы. Например, введем «2+9». Для выполнения команды необходимо одновременно нажать комбинацию клавиш «Shift»+«Enter» или «Enter» на вспомогательной (цифровой) части клавиатуры. Результат вычисления появится в следующей ячейке. Обратим внимание на то, что первое вычисление в любой сессии пакета занимает большее время, чем последующие вычисления выражений аналогичной сложности, поскольку при этом подгружается ядро пакета, в котором хранятся результаты всех вычислений текущей сессии. Ячейки ввода автоматически нумеруются и обозначаются «In[n]», где n – порядковый номер ячейки, выходные ячейки обозначаются «Out[n]». Даже если ячейки удаляются из рабочего окна, результаты их вычислений сохраняются в ядре и результат их вычислений можно увидеть на экране, выполнив команду «Out[n]» с нужным номером (например, можно набрать «Out[1]» и нажать «Shift»+«Enter»). Итак, «Mathematica» относится к языкам-интерпретаторам, все команды обрабатываются в ядре пакета в последовательности их исполнения (при нажатии комбинации клавиш «Shift»+«Enter»), и результат каждого вычисления не зависит от положения соответствующей ячейки в рабочем окне, а только от порядка его выполнения относительно других команд.

Перейдем к описанию работы с математическими выражениями. Арифметика: сложение «+», вычитание «–», умножение « », деление «/», возведение в степень «^». Отметим, что операцию « » можно заменять пробелом (результат вычисления в пакете выражения «4 5» отличается от вычисления «45»), а в случае когда числовой множитель стоит перед символьным выражением, никакой знак ставить не нужно. Например, выражения «5 x», «5 x» и «5x» эквивалентны, причем рекомендуется ис-

67

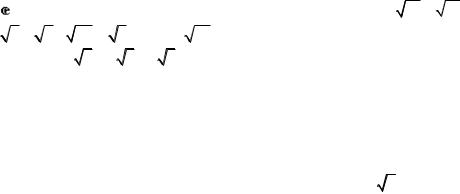
пользовать последнюю запись для облегчения чтения кода. Выражения «5x» и «x5» не эквивалентны: первое есть произведение числа 5 и переменной x, а второе означает независимую переменную x5, для перемножения в последнем случае необходимо вставить пробел «x 5». Выполните для сравнения команды «3x + 5x» и «x3 + x5». Часто для улучшения читаемости вводимых выражений используется традиционная математическая нотация. Возведение в степень при этом задается не как «x^3», а с помощью комбинации клавиш «Ctrl»+«^» после ввода «x». Операция деления представляется в виде дроби с помощью комбинации «Ctrl»+«/». Квадратный корень вводится с помощью комбинации клавиш «Ctrl»+«@».

Обратите внимание, что пакет «Mathematica» выделяет введенные символы различными цветами – числа отображаются черным цветом, переменные «x», «x2», «x5» – синим. Это означает, что для пакета величины «x», «x2», «x5» (выделенные синим цветом) не известны или не определены, а числа являются известными величинами.

Для большинства операций в пакете возможны различные способы их реализации. Например, сложение можно задавать, как было показано выше, с помощью «+», а можно с помощью функции «Plus[]» – выполните «Plus[2,9,–1,x]». Аналогично умножение можно представить иначе, как «Times[3,x,y]», возведение в степень как «Power[x,3]» и так далее.

Пакет «Mathematica» позволяет работать с логическими выражениями (относительно которых можно сказать, что они истинны «True» или ложны «False»). Для сравнения выражений применяются операторы «==» – равны ли выражения, «! =» – не равны, «<» – меньше, «>» – больше, «<=» – меньше или равно, «>=» – больше или равно. Сравните результаты выполнения команд «5<3», «7==7», «4>1», «12<=19». Выясните

с помощью логических операций пакета, что больше, 13 − 12 или

растания 5 2 , 4 3 , 3 6 . Для манипулирования логическими выражениями используются операторы логического «И» – «&&» и логического «ИЛИ» – «||». Отметим, что последовательность символов «! =» автоматически преобразуется пакетом в знак «≠ », «<=» – в знак «≤», «>=» –

взнак «≥ » и так далее.

Впакете реализована работа с точными и приближенными типами

Заметим, что «π » и «» отображаются черным цветом, хотя являются символами. Это означает, что пакету известны их значения.

68

После выполнения команды по вводу точных выражений они могут быть упрощены сокращением дроби (выполните команду «14/20»), вычислением точного значения функции, но приведенные выше выражения не преобразуются. Для перехода к их приближенному значению в числовых выражениях необходимо ставить десятичную точку, например,

« 3.0 » или просто « 3. », но что делать с «π »? Можно умножить или разделить на «1.0», можно добавить «0.0», но существует более удобный способ – использовать встроенную функцию пакета. Все встроенные функции начинаются с заглавных букв, а аргумент указывается в квадратных скобках (как, например, уже встречавшаяся функция «Out[1]»). Для приближенного вычисления значения выражений используется функция «N[]» (от английского numerical), например, «N[π ]». Многие функции пакета имеют дополнительные необязательные аргументы и могут вызываться с разным числом аргументов. Функция «N[]» имеет второй необязательный аргумент, задающий количество цифр для вывода приближенного значения: выполните команду «N[π ,150]», в результате в ячейке вывода появится 150 значащих цифр числа π .

Для ввода греческих букв и специальных символов с клавиатуры (часто это оказывается быстрее, чем делать вставку соответствующего знака из открытого окна палитры) используется следующая последовательность действий: нажимается клавиша «Esc» (на экране появится символ «#»), вводится соответствующая буква латинского алфавита, например, «p» и снова нажимается «Esc» (последовательность «#p#» автомати-

чески преобразуется в «π »). Для ввода экспоненты надо набрать «Esc», «ee», «Esc» (если набрать только один раз «e», то результатом будет греческая буква «ε »), для ввода мнимой единицы – «Esc», «ii», «Esc» (на экране она отображается как «»).

В арифметических выражениях используются такие типы данных, как Integer, Rational, Real. Для выяснения типа выражения применяется функция «Head[expr]» (заголовок). Выясните, какое значение она возвращает в следующих случаях: Head[5], Head[7/3], Head[3.14159], Head[π ]. «Mathematica» дает каждому выражению и каждой его части свой тип, например, выражение «2+π » имеет заголовок «Plus», выраже-

ние «Sin[π +3]» – заголовок «Sin».

В пакете доступны стандартные математические функции: тригонометрические – «Sin[]», «Cos[]», «Tan[]»,»Cot[]», обратные тригономет-

рические функции –»ArcSin[]», «ArcCos[]», «ArcTan[]», «ArcCot[]», из-

69

влечение арифметического квадратного корня – «Sqrt[]», экспонента – «Exp[]», логарифм по основанию b – Log[b, ]» (натуральный логарифм

«Log[]»). Вычислите, например, «Sin[ 3π ]», «Log[5e]». 4

Пакет «Mathematica» позволяет работать и с комплексными числами. Для ввода мнимой единицы, как упоминалось выше, используется последовательность нажатия клавиш «Esc», «ii», «Esc». Найдите квадрат мнимой единицы «». Вычислите также приближенное значение комплекс-

ного числа вида . Функции, позволяющие находить действи-

тельную и мнимую части комплексного числа, записываются соответственно как «Re[]» и «Im[]». Примените их к результату предыдущего вычисления.

«Mathematica» предоставляет массу средств рисования графиков функций. Универсальная функция, которая для этого используется, – это функция «Plot[]». Она имеет два обязательных аргумента: саму функциональную зависимость, график которой надо отобразить, и интервал изменения аргумента, например, для рисования параболы необходимо выполнить команду «Plot[x2,{x,–2,3}]». Второй аргумент {x,–2,3} имеет следующий смысл – x есть переменная, которая меняется от –2 до 3. Постройте график функции y = sin(x) на отрезке [–π ; 2π ].

Для изображения на одном рисунке графиков нескольких функций первый аргумент представляется в виде {x2,x3,Exp[2x]} (такая конструкция называется списком), то есть в фигурных скобках перечисляются исследуемые функции: «Plot[{x2,x3,Exp[2x]},{x,–2,3}]». Результат, полученный в «Mathematica 7.0», будет выглядеть, как на рис. 1.6, а. Обратите внимание, что графики перечисленных функций изображаются различными цветами, выбираемыми пакетом автоматически.

К необязательным аргументам функции «Plot[]» относятся опции, управляющие способами отображения графиков. Рассмотрим основные дополнительные аргументы. При рисовании графиков функций «Mathematica» автоматически выстраивает масштаб области вывода и соотношение ее сторон для наиболее наглядного, с точки зрения разработчиков пакета, представления результата. При этом некоторые точки графика функции могут вообще не попасть в область отображения. Для задания собственных размеров области рисунка используется опция «PlotRange». Для того чтобы вывести все возможные точки графика функции, этой опции надо придать значение «All»: Plot[{x2,x3,Exp[2x]},{x,–2,3},

70