
книги / Остаточные напряжения в полимерных композиционных материалах
..pdf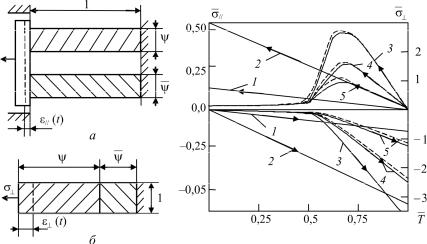
Рис. 6.1. Схема деформирования |
Рис. 6.2. Приведенные напряжения |
||||||
композита: а – вдоль; |
|
в композите: 1, 2 – продольные: |
|||||
б – поперек волокна |
(1) |
–4 |
(2) |
–2 |
= 0,1 (1), 0,5 (2); |
||
|
Em |
= 10 , |
Em |
= 10 ; ψ |
|||
|
3–5 – поперечные: Em(1) |
= 0,01, Em(2) = 1; |
|||||
|
|
ψ = 0,1 (3); 0,5 (4); 0,7 (5). |
|||||
|
--- – расчет по (6.31), |
|
|
– по (6.30) |
|||
|
|
|
|||||
E (N ) = Em Ea [Ea ψ+ Emψ]−1 ;
εT = T (αmψ+ αa ψ)dT; E(1) = Em(1)Ea Ea ψ+ Em(1)ψ −1 ;
TH
E(2) = Em(1) + Em(2) Ea Ea ψ+ (Em(1) + Em(2) ) −1 − E(1);
T
εT(1) = εT(2) = (αm ψ+ αa ψ)dT; Em =Em(1) + Em(2) N.
TH
Подставив данные выражения в (6.23)–(6.26), получим
161

|
эg |
T |
|
(1) |
+ E |
(2) |
|
|
|
ψ]dT; |
σ |
(T ) = − |
E |
|
|
N (T ) [αmψ+ αa |
|||||
|
|
TH |
(1) + E(2) N )εэ (T ) + σэg (T ); |
|
||||||
|
σэh (T ) = (E |
|
||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
σжg (T ) = − Em Ea [Ea ψ+ Emψ]−1 dT; |
|
|||||||||
|
|
TH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
εж (T ) + σжg (T ), |
|
σжh (T ) = E E [E ψ+ E ψ] |
|
|||||||||
|
|
m |
a |
|
a |
|
m |
|
k |
|
(6.29)
(6.30)
где εэ (Tk ) = −σэc (Tk ) E(1) + E(2) −1; εж (Tk ) = −σжg (Tk ) ψ(Em(1) + Em(2) )+ ψEa −1 .
Точное решение находим, как и ранее, вычислял систему (6.26) с учетом того, что
σ(T ) = σa (T ) = σm (T ); ε(T ) = εa (T )ψ+ εm (T )ψ.
После подстановки данных соотношений в (6.26) и некоторых преобразований получим выражения для напряжений, совпадающие с «жесткостными» (6.30). Таким образом, соотношения (6.17) точно описывают макроповедение композиционного материала для простейших вариантов осреднения свойств. Уравнения (6.16) дают некоторую ошибку при поперечном деформировании. На рис. 6.2 показаны кривые приведенных напряжений, рассчитанные численно по (6.26), (6.29), (6.30). На рис. 6.2, 6.3 обозначено:
σ = σ (αa Eaθk ); Em(i) = Em(i)
(αa Eaθk ); Em(i) = Em(i)  Ea ; αm = αm
Ea ; αm = αm  αa ; θk = TH − Tk ; θg = TH − Tg ;
αa ; θk = TH − Tk ; θg = TH − Tg ;
σ = 2 σэ (T ) − σж (T )
 σэ (Tk ) − σж (Tk ) −1 ; T = (TH − T )
σэ (Tk ) − σж (Tk ) −1 ; T = (TH − T ) θk .
θk .
Кривые 1, 2 отражают изменение напряжений при растяжении вдоль волокна. Характеристики примерно соответствуют органопластику с анизотропным волокном, имеющим поперечный модуль, соизмеримый с модулем матрицы. Графики 3–5 соответствуют напряжениям в поперечно деформируемом материале для различных значений ψ. Динамика изменения относительной невязки σ представлена на рис. 6.3.
162
а б
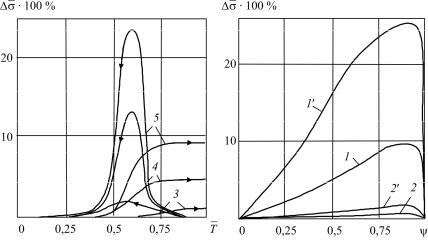
Рис. 6.3. Погрешность расчета напряжений по (6.29) в зависимости от:
а– температуры (обозначения те же, что на рис. 6.2);
б– объемного содержания волокна. 1 – Em(1) = 0,001, Em(2) = 1;
2 – Em(1) = 10–4, Em(2) = 10–2; 1′, 2′ – то же для нагрева
Видно, что максимальная погрешность наблюдается в интервале стеклования. Ее величина возрастает с ростом ψ и достигает максимального значения при ψ = 0,96. В интервале температур, соответствующем условиям эксплуатации готового изделия (ниже Tg2 ), ошибка расчета не превышает 10 %. Для пластиков с изотропным волокном (стекло-, боропластик и др.) с EM(2) << 1 максимальная не-
вязка поперечных напряжений не превышает 3 % (см. рис. 6.3, б, кривая 1). Это говорит о том, что соотношения (6.16) можно применять для описания поведения композиционных материалов в исследованном диапазоне изменения свойств, тем самым значительно сокращая объем численных расчетов по отысканию неизвестных термомеханических констант (см. разд. 4.3).
163
6.2. ПРОГНОЗИРОВАНИЕ ЭФФЕКТИВНЫХ ХАРАКТЕРИСТИК
ВОЛОКНИСТОГО КОМПОЗИТА НА ОСНОВЕ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ
Одной из основных задач механики композиционных материалов является определение механических характеристик композита по свойствам его компонентов. Элементы конструкций из композиционных материалов составляются обычно из различно ориентированных однонаправленно армированных слоев, уложенных в определенной последовательности, поэтому в основе методов расчета и проектирования таких конструкций лежат механические характеристики однонаправленно армированного слоя, которые требуется определить экспериментально или расчетным путем. Механическое поведение композитов значительно зависит от времени и температуры, что может быть обусловлено в том числе и стеклованием или размягчением связующего.
Термомеханическое поведение композиционных волокнистых материалов при малых деформациях традиционно описывается в рамках линейной анизотропной теории упругости [91, 84, 107, 125]. Проблеме прогнозирования термомеханических характеристик однонаправленных волокнистых ПКМ по известным упругим свойствам и коэффициентам температурного расширения волокон и связующего посвящено значительное число работ [2, 5–7, 11–13, 55, 64, 65, 88, 99, 108–112, 115–117, 142, 145, 146].
Известно, что свойства полимерных композитов существенно зависят от температуры [86, 90, 92, 128, 140]. Экспериментальные исследования свойств компонентов композита в широком температурном диапазоне приведены в работах [70, 90, 92, 140]. Во многих исследованиях показано соблюдение принципа температурно-вре- менной аналогии для композита и его компонентов в условиях неизменного релаксационного состояния [81, 89, 90, 92, 97, 124, 140, 159]. В общем случае, когда рассматриваемый температурный диапазон включает релаксационный переход связующего из высокоэластического в стеклообразное состояние, прямое применение тради-
164
ционных моделей теории термовязкоупругости затруднено очевидным несоблюдением принципа температурно-временной аналогии,
ивозникает необходимость в разработке специальных подходов.
Врамках предложенной в данной работе термомеханической модели поведения композиционных материалов вида (6.3) задача прогнозирования эффективных характеристик существенно упрощается. В соответствии с принятыми гипотезами следует определить две группы эффективных параметров: для связующего в высокоэластиче-
ском состоянии – Cijkl(1) (T ) , αii(1) (T ) и в застеклованном состоянии – Cijklg (T ) , αiig (T ) . Механическое поведение большинства типов волокон
(борное, углеродное, стекловолокно), как сказано выше, можно считать упругим и не учитывать температурную зависимость модуля упругости. В случае анизотропного органического волокна, обладающего ярко выраженным вязкоупругим поведением, вводится гипотеза о том, что при температурах ниже температуры стеклования связующего T < Tg его модуль Юнга совпадает с мгновенным модулем,
а при T > Tg – с длительным модулем.
6.2.1. Постановка задачи
Рассматриваются однонаправленно армированные композиционные материалы, волокна которых являются упругими изотропными (стекловолокно), упругими монотропными (борное и углеродное волокно) или упругими монотропными с зависимостью от температуры (органическое волокно) материалами, а связующее считается изотропным материалом, поведение которого описывается моделью (3.2) (например эпоксидное связующее ЭДТ-10).
Общая постановка краевой задачи теории термоупругости для тела, занимающего область V ≡ V a V m с границей S , где V a – область, принадлежащая волокну, V m – область, принадлежащая связующему, включает в себя для t > 0 :
уравнения равновесия
ˆ |
+ |
f (x,t ) |
= |
|
|
|
|
|
divσ(x,t ) |
|
|
0, |
x |
|
V , |
(6.31) |
165
геометрические соотношения теории малых деформаций
ˆ |
|
|
u(x,t ) + ( |
|
|
|
T |
|
|
|
|
|
|
2ε(x,t ) = |
|
|
u |
(x,t )) , |
|
x |
|
V , |
(6.32) |
||||
граничные условия |
|
|
|
|
|
|
|
|
|
|
|
||
|
u(x,t ) = U(x,t ), |
|
x Su , |
|
|
(6.33) |
|||||||
|
ˆ |
|
|
n(x) = p(x,t ), |
x |
|
Sσ. |
|
|
(6.34) |
|||
|
σ(x,t ) |
|
|
|
|
||||||||
Для замыкания системы уравнений (6.31)–(6.34) необходимо записать определяющие соотношения. В моделях упругого приближения (3.2), (6.3), описывающих термомеханическое поведение связующего и всего композита соответственно, предполагается необходимость определения эффективных термоупругих характеристик отдельно для стеклообразного и высокоэластического состояний связующего. Тогда для связующего в высокоэластическом состоянии
σij |
|
(1)m |
(T ) − |
2 |
G |
(1)m |
|
θ(x)δij |
+ 2G |
(1)m |
(T )εij (x) − |
(x) = B |
|
3 |
|
(T ) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
−3B(1)m (T )εTm (x,T )δij , |
x V m , |
|
|
|
|
|
(6.35) |
|||||||||
при этом для волокна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)a |
(T ) |
εkl (x) − |
a |
|
x V |
a |
. |
(6.36) |
||||||
|
σij (x) = Cijkl |
εTkl (x) , |
|
|
|||||||||||||
Для связующего в стеклообразном состоянии |
|
|
|
|
|
|
|||||||||||
σij |
|
gm |
(T ) − |
2 |
G |
gm |
|
θ(x)δij + |
2G |
gm |
(T )εij (x) − |
|
|||||
(x) = B |
|
3 |
|
(T ) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3Bgm (T )εTm (x,T )δij , x V m , |
|
|
|
|
(6.37) |
||||||||||
при этом для волокна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
σij (x) = Cijkl |
|
|
|
|
|
|
x V |
|
. |
(6.38) |
||||||
|
(T ) εkl (x) − εTkl |
(x) , |
a |
||||||||||||||
|
|
|
ga |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
166
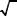
В соотношениях (6.31)–(6.38) σˆ, εˆ – тензоры напряжений и деформаций с компонентами σij и εij соответственно; u,f ,n – векторы
перемещений, объемных сил и внешней единичной нормали к поверхности S с компонентами ui , fi ,ni ; x – радиус-вектор произвольной
точки тела, имеющий компоненты xi ; U – заданный на части Su границы S вектор перемещений с компонентами Ui ; p – заданный на части Sσ границы S вектор поверхностных сил с компонентами pi ; Su Sσ ≡ S . Для упругих волокон (стекло-, боро- и углеволокна) мат-
рицы упругости в соотношениях (6.36), (6.38) по форме совпадают. При рассмотрении материала композита в некотором малом объе-
ме можно считать его неоднородным. Но в этом случае задача описания его свойств становится очень сложной. Для преодоления этой трудности вводится гипотеза континуума [58]. Она включает процедуру осреднения, посредством которой структура и состояние материала идеализируются таким образом, что материал считается однородным, у него присущие однородной среде характерные свойства одинаковы во всех точках. Основная задача состоит в использовании процедуры осреднения для предсказания эффективных свойств идеализированной однородной средычерезсвойствафазигеометрическиехарактеристики.
Рассматриваем однонаправленно армированный слой как неограниченную непрерывно армированную среду со структурой, образованной выпрямленными и одинаково ориентированными цилиндрическими волокнами с равными круговыми поперечными сечениями. Пространство между волокнами заполнено связующей средой – матрицей, характеристики которой отличны от характеристик волокон.
Выделим из данной среды ячейку симметрии (будем рассматривать гексагональную укладку волокон) – элементарный объем (рис. 6.4). Предполагаем, что в границах данного объема градиент внешнего поля воздействий изменяется незначительно.
Относительное объемное содержание волокна в композите через параметры ячейки периодичности можно выразить соотношением
ψ = |
2V m |
= |
πR2 |
. Для гексагональной упаковки a = |
b |
. |
|
2ab |
3 |
||||
V m + 2V a |
|
|
|
|||
167
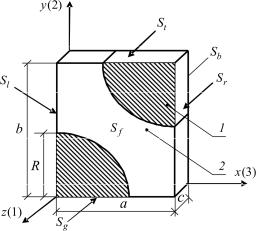
Рис. 6.4. Ячейка периодичности и принятая система координат: 1 – наполнитель (волокно); 2 – матрица материала; a , b , с – ширина, высота и глубина ячейки; R – радиус волокна; S f , Sb , Sl , Sr , Sg , St – передняя, задняя, левая, правая, нижняя и верхняя грани ячейки периодичности соответственно
Исходя из структуры однонаправленного композита с гексагональной укладкой волокон и согласно гипотезе континуума, материал можно считать однородной средой, которая имеет ось упругой симметрии, совпадающую с направлением волокон, т.е. но трансвер- сально-изотропный (монотропный). Таким образом, упругое поведение композита характеризуется пятью независимыми константами: модулями упругости E1 и E2 , соответствующими направлениям вдоль и поперек волокон, коэффициентами Пуассона ν12 и ν23 и оператор-
ным модулем сдвига G12 , которые требуется определить из задач
(6.31)–(6.36) или (6.31)–(6.34), (6.37), (6.38).
Опишем вычислительные эксперименты, которые необходимо поставить для исследования трехмерной ячейки периодичности, чтобы найти термоупругие эффективные характеристики композита: продольную деформацию вдоль направления волокон; поперечную деформацию в плоскости, перпендикулярной направлению волокон;
168
сдвиговую деформацию вдоль направления волокон; свободную температурную деформацию.
1. Продольная деформация ячейки периодичности.
Для данного случая деформирования необходимо реализовать следующие условия на границах ячейки периодичности:
u1 (x) u2 (x) u3 (x)
= 0, |
x S |
; |
u (x) = U 0 , |
x S |
f |
; |
|
|
b |
|
1 |
1 |
|
|
|
= 0, |
x Sg ; |
u2 (x) = U2 , |
x St ; |
||||
= 0, |
x Sl ; |
u3 (x) = U3 , |
x Sr |
; |
|||
σ12 (x) = σ13 (x) = 0, |
x S f ; |
|
|
(6.39) |
|||
|
|
|
|||||
σ12 (x) = σ23 (x) = 0, |
x St ; |
|
|
|
|||
σ13 (x) = σ23 (x) = 0, |
x Sr . |
|
|
|
|||
Величина U10 задается, а U2 и U3 – неизвестные параметры, по-
лучаемые из решения задачи.
Для описания механических свойств композита введем понятие средних напряжений и средних деформаций:
σij |
= |
1 |
|
σij (x)dV ; |
(6.40) |
|
|
|
|||||
|
V |
|
V |
|
||
|
|
|
|
|
|
|
εij |
= |
1 |
|
εij (x)dV. |
(6.41) |
|
|
|
|||||
|
|
V |
|
V |
|
|
|
|
|
|
|
|
|
Деформация композита в продольном направлении постоянна и запишется следующим образом:
ε110 = ε11 |
= |
U10 |
. |
|
|||
|
|
c |
|
Из решения задачи на ячейке периодичности необходимо найти следующие величины: осредненные продольные напряжения  σ11
σ11 и осредненные поперечные деформации:
и осредненные поперечные деформации:
169

ε22 |
= |
U2 |
; |
ε33 |
= |
U3 |
. |
|
|
||||||
|
|
b |
|
|
a |
||
При этом непосредственно из решения должно следовать
 σ22
σ22  =
=  σ33
σ33  =
=  σ12
σ12  =
=  σ13
σ13  =
=  σ23
σ23  = 0.
= 0.
Эффективные характеристики композита: модуль упругости E1 и коэффициент Пуассона ν1 определяются из следующих соотношений:
E1 =  σ11
σ11
 ε110 ; ν12 =
ε110 ; ν12 =  ε22
ε22 
 ε110 ; ν13 =
ε110 ; ν13 =  ε33
ε33 
 ε110 .
ε110 .
В силу трансверсальной изотропии свойств непосредственно из решения должно получиться выполнение равенства ν12 = ν13 .
2. Поперечная деформация ячейки периодичности.
Для данного случая деформирования необходимо реализовать следующие условия на границах ячейки периодичности:
u1 (x) = 0, |
x Sb ; u1 (x) = U1 , |
x S f ; |
|
|
u2 (x) = 0, |
x Sg ; u2 (x) = U20 , |
x St ; |
|
|
u3 (x) = 0, |
x Sl ; u3 (x) = U3 , |
x Sr ; |
(6.42) |
|
σ12 (x) = σ13 (x) = 0, |
x S f ; |
|
||
|
|
|||
σ12 (x) = σ23 (x) = 0, |
x St ; |
|
|
|
σ13 (x) = σ23 (x) = 0, |
x Sr . |
|
|
|
Величина U20 задается, а U1 и U3 – неизвестные параметры, по-
лучаемые из решения задачи.
Деформация композита в поперечном направлении постоянна и запишется следующим образом:
ε022 = ε22 |
= |
U20 |
. |
|
|||
|
|
b |
|
170
