книги / Остаточные напряжения в полимерных композиционных материалах

трудняется инерционностью процессов теплопередачи в полимерах и невозможностью полной компенсации несовместности деформирования, обусловленной различием свойств материалов изделия и технологического оборудования. Один из путей решения данной проблемы – приложение на стадии охлаждения полимерного изделия дополнительной, переменной во времени внешней нагрузки. В разделе предлагается и анализируется методика расчета оптимального силового регулирования остаточных напряжений аморфных стеклующихся сетчатых полимеров.

Для описания термомеханического поведения материала используются определяющие соотношения в упругом приближении (3.3), (3.4), записанные в сокращенной форме:

в стеклообразном и высокоэластическом состояниях соответственно; εˆ (t) = εˆ − εˆT ; εˆ , εˆT – тензоры полных и температурных деформа-

T (t )

ций соответственно; εTij = αij (τ)dT (τ); αij = αδij ; α – коэффициент

T0

температурного расширения; δij – символ Кронекера; σˆ (t) – тензор напряжений; T (t) – температура; t, τ – время. Соотношения (7.1) подразумевают существование связи между степенью стеклования N и температурой T. Для этого, в частности, можно использовать одну из формул (2.7)–(2.9)

Пусть изделие, занимающее область Ω с границей S, охлаждается от температуры TH за счет теплообмена с окружающей средой. При остывании на части его границы Sσ действует внешняя дополнительная нагрузка P(x,t) , не зависящая от температуры и не влияющая на теплообмен. Приняв допущение об отсутствии источников тепловыделения, можно разделить проблему определения остаточно-

211

го напряженно-деформированного состояния конструкции на две несвязанных задачи. Первая из них – задача теплопроводности

где t* – время перехода всего изделия в стеклообразное состояние; a2 – коэффициент температуропроводности, a2 = λ / (cρ); h – коэффициент теплоотдачи; x, n – радиус-вектор и вектор единичной нормали кповерхностисоответственно, Ts – температураокружающейсреды.

Результаты решения (7.12)–(7.16) используются в задаче расчета напряженно-деформированного состояния, при этом система уравне-

где u – вектор перемещений; U(x,t) – перемещения, заданные на части поверхности Su ; P(x,t) – управляющая нагрузка.

Будем полагать, что внешнюю нагрузку можно представить в виде произведения функций времени и координат

212

где px (x) – заданная функция; h – функция Хевисайда. Тогда задача

управления формулируется следующим образом: найти управление p(t), сообщающее минимум функционалу

Ω

при ограничениях (7.11)–(7.21), где σ*(x) ≡ σˆ (x,t) , t > t* – поле технологических остаточных напряжений (решение (7.11)–(7.21)); σˆ R (x,t) – задаваемое по условиям эксплуатации распределение остаточных напряжений (в частности, отсутствие остаточных напряжений соответствует случаю σˆ R (x,t) = 0); F(σˆ ) – некоторая скалярная функ-

ция тензора напряжений. В качестве такой функции может выступать один из инвариантов, например, интенсивность напряжений:

Покажем, что решение задачи определения напряженно-дефор- мированного состояния (7.11), (7.17)–(7.21) можно представить в виде следующей суперпозиции:

где σˆT (x,t) – решение задачи при отсутствии внешнего воздействия:

σˆ P (x,t) – решение задачи в условиях, когда не учитывается температурная деформация:

Для этого преобразуем соотношения (7.11) к более компактному виду:

213

Здесь и далее радиус-вектор x опущен для сокращения записи. С учетом (7.22) и в предположении непрерывности p(t) разложим

полный дифференциал dεˆ (τ) по двум независимым переменным – нагрузке p(τ) и температуре T (τ) :

где εˆ p (τ) – приращение тензора деформаций под действием единичного приращения внешней нагрузки в момент τ при отсутствии температурной деформации (α = 0); dεˆT (τ) – полный дифференциал

тензора деформаций без учета дополнительного нагружения (p(t) = 0). После подстановки (7.28) в (7.27) получим

214

Первые два слагаемых в (7.29) представляют собой решение задачи (7.25) σˆ P (t) , третье – решение задачи (7.26) σˆT (t) .

Используя (7.29), преобразуем (7.23) к виду

Ω

при этом управляющая нагрузка присутствует только в первом слагаемом. Из (7.22), (7.29) следует

Для численного решения (7.30) осуществим дискретизацию во времени и пространстве. Обозначим через Me , Mt количество эле-

ментов и шагов по времени соответственно. Под элементом Ωk подразумевается часть области Ω , с осредненными по ней деформация-

Me

ми и напряжениями, причем Ω = Ωk . Применяя левую формулу

k =1

прямоугольников для вычисления интеграла в правой части (7.31), с учетом (7.22) получим

j=0

215

где

тензор остаточных напряжений σkP* в k-м элементе с учетом снятия на-

грузки на последнем шаге (второе слагаемое в правой части (7.33)). Таким образом, благодаря линейности определяющих соотношений удается в матрице влияния Ψ разместить полную информацию об «управляемости» остаточного напряженно-деформированного состояния дополнительной нагрузкой.

Задача (7.30) с учетом (7.32) сводится к решению системы урав-

k=1

Возможны варианты, когда функция управления P(t) аппроксимируется одним из известных методов (степенной ряд, кусочнолинейный полином, сплайны). Это позволяет понизить порядок системы (7.34) и добиться большей устойчивости решения.

Технология численного расчета оптимального силового воздействия, в соответствии с приведенными выше выкладками, состоит из следующих этапов:

1. Решение задачи (7.25) – определение поля остаточных напряжений σˆTk * в конструкции, находящейся в «естественных» условиях

технологического процесса охлаждения без дополнительных внешних воздействий. Остаточные напряжения при этом формируются только за счет неравномерности пространственно-временного рас-

216

пределения температурных деформаций в объеме охлаждаемой конструкции.

2. Расчет матрицы Ψ. Для этого решается задача охлаждения вида (7.26), из которой исключены температурные напряжения и деформации. Учитывается лишь влияние температуры, найденное из решения системы (7.12)–(7.16), на изменение степени стеклования N . На каждом шаге по времени прикладывается дополнитель-

го приращения нагрузки в полностью охлажденном изделии. 3. Формирование и решение системы (7.34).

Изложенные выше рассуждения допускают простое обобщение для варианта конечного числа независимых внешних воздействий. Можно показать, что в качестве управляющих объектов, помимо внешней нагрузки P(x,t) (силовое воздействие, см. (7.21)), могут

выступать в том числе и граничные перемещения U(x,t) (кинематическое воздействие, см. (7.20)), а также их комбинации.

Следует также отметить, что количество решений задачи термоупругости, необходимых для формирования матрицы Ψ и расчета σˆTk * , составляет 2Nt , т.е. всего в 2 раза превышает трудоемкость ре-

шения прямой задачи определения остаточного напряженно-дефор- мированного состояния в свободной от внешнего воздействия охлаждаемой конструкции.

7.4.2. Иллюстративный пример: минимизация остаточных напряжений в пакете стержней

Как пример практического использования полученных зависимостей при совместном, кинематическом и силовом управляющем воздействии далее приводится решение следующей модельной задачи.

217

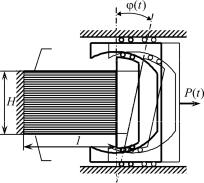
Пакет совместно деформирующихся полимерных стержней охлаждается от температуры TH благодаря теплообмену с окружающей средой по границе S3 ( x = H , граничные условия III рода (7.15)) до температуры TK . Граница S0 (x = 0) адиабатическая (граничные условия вида (7.16)). Сосредоточенная сила P(t) и угловое перемещение φ(t) позволяют управлять деформацией пакета в процессе охла-

ждения. Предполагаем, что трение между слоями пакета, а также напряжения в направлениях, нормальных к продольному, отсутствуют. Данная гипотеза соответствует одноосному напряженному состоянию, для каждого стержня в пакете физические уравнения (7.11) пре-

E1, E2 – модули Юнга материала в высокоэластическом и стеклооб-

разном состояниях соответственно. Будем также полагать, что в начальный момент времени конструкция находится в естественном ненапряженном состоянии, т.е. σ(x,0) = 0, x [0,H].

Математически граничные условия задачи об определении напря- женно-деформированного состояния, соответствующие показанной на рис. 7.17 схеме, представляются в виде

Рис. 7.17. Расчетная схема модельной задачи

218

Для получения численного решения проведем пространственновременную дискретизацию. Обозначим через Me количество стерж-

ней. Время охлаждения разобьем на Nt интервалов, в каждом из которых нагрузка P(t) и угловое перемещение φ(t) аппроксимируются кусочно-линейными полиномами, причем P(0) = φ(0) = 0 . Представление управляющих функций в виде ломаных с относительно малым числом узловых точек позволяет избежать появления осцилляций, возникающих в случае, когда неизвестные значения определяются на каждом шаге по времени. В свою очередь, 1-й интервал

Будем решать задачу минимизации остаточных напряжений. Это означает, что в соответствии с принятыми обозначениями σkR = 0,

k = 1, Me . Тогда (7.34) преобразуется к системе 2Nt уравнений вида

Соответствующие выкладки приводят к решению системы уравнений [A]{c} = {d} относительно вектора {c}, где

219

Далее представлены результаты расчета для материала с физи- ко-механическими свойствами, близкими к характеристикам эпоксидной смолы ЭДТ-10 (см. гл. 4). Вычисления проводились для трех вариантов дополнительного воздействия: силового (φ(t) = 0 ), кинематического (P(t) = 0) и совместного, при TH = 160 °C ; TK = 20 °C;

H = 0,05 м; Me = 40; Nt = 10 (вариант 1) и Nt = 20 (вариант 2). Об-

щее количество шагов по времени в обоих вариантах одинаково

Nt

и равно Mtl = 400.

l=1

Результаты расчета представлены в безразмерном виде: P – безразмерная внешняя нагрузка, P = P / (K H ) ; σ – безразмерное

напряжение, σ = σ / K , где K = α(TH − TK )(E1 + E2 ) .

На рис. 7.18, 7.19 отображены результаты, полученные в первом варианте расчета.

220