
книги / Остаточные напряжения в полимерных композиционных материалах
..pdfвить, для какой из фаз следует применять уравнение в дифференциальной форме, для какой в конечной. Считается, что вещество в каждом из релаксационных состояний (высокоэластическом либо стеклообразном) идеально упруго, его физико-механические характеристики неизменны, а переход происходит скачком. Модель основана на чисто феноменологическом подходе и позволяет добиться качественно верного описания эффектов стеклования и размягчения при предельно упрощенном наборе материальных констант. Определяющие соотношения в этом случае принимают вид
σ |
= |
ε |
(T |
< g |
); |
σ |
|
= 1 |
ε |
|
(T |
≥ g |
), |
|
БГ |
|
E g , |
T |
|
БГ |
E |
|
, |
T |
(2.35) |
где Eg , E1 – модули Юнга материала в стеклообразном и высокоэластическом состояниях соответственно. Основную погрешность при расчетах по данной модели будет вносить допущение о скачкообразности перехода из мягкой в твердую фазу.
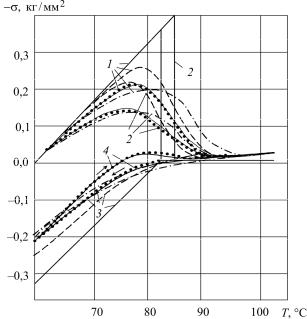
На рис. 2.12 показаны кривые напряжений в защемленном образце из эпоксидной смолы ЭДТ-10 (одноосный образец с равными нулю перемещениями на обоих концах). Режим изменения температуры включает нагрев от 60 до 105 °С с последующим охлаждением до исходной точки. Экспериментальные кривые для двух значений скорости изменения температуры построены по данным работы [135]. При расчете по формулам (2.35) принималось, что E g = E1 (100 °С) + E2 (60 °C). Для сравнения приведен расчет по со-
отношениям (2.5). Значения входящих в (2.5) констант взяты из эксперимента разд. 2.5; полагалось, что стеклование образца до начала охлаждения было свободным (без нагрузки), поэтому интеграл в правой части (2.5) обнуляется и напряжение в образце на стадии повышения температуры описывается следующей формулой:
σH = − E1 (T (t )) + E2 (T (t ))N (T (t )) εT (T (t )). |
(2.36) |
При охлаждении материала физические уравнения (2.5) принимают вид
81
σС = − E1 (T (t )) + E2 (T (t ))N (T (t )) εT (T (t )) −
N(t ) |
|
|
− εT (T (τ))dN (τ)E2 |
(T (t )). |
(2.37) |
0 |
|
|
Сравнение результатов анализа по (2.35)–(2.37) с результатами эксперимента (см. рис. 2.12) показывает, что неучет плавности релаксационного перехода приводит к погрешности по напряжениям порядка 70 % на кривой разогрева. Это накладывает определенные ограничения на использование упрощенной модели И.И. Бугакова
Рис. 2.12. Напряжения в защемленном образце из ЭДТ-10: 1 – нагрев со скоростью T = 1,5 °С/мин; 2 – 0,5 °С/мин; 3 – охлаждение с T = –1,5 °С/мин; 4 – повторный нагрев;
– модельИ.И. Бугакова, - - - - – упругое приближение(2.5), - - - - – модель Дж. Максвелла, – эксперимент [36],
____ – вязкоупругая модель (2.31)
82
в расчетах технологического напряженно-деформированного состояния изделий из стеклующихся материалов.
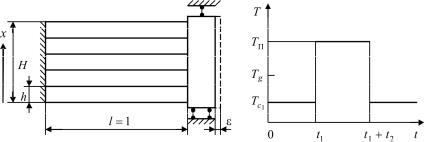
В качестве примера проведем расчет остаточных технологических напряжений в пакете из n эпоксидных стержней единичного поперечного сечения (рис. 2.13). Охлаждение пакета происходит от T = TП за счет конвективного теплообмена с окружающей средой
с температурой Tc (t ), в результате чего в стержнях возникают про-
n
дольные напряжения σi , а общее усилие равно нулю σi = 0.
i=1
Деформирование происходит совместно, поэтому εi = ε. Пусть тем-
пература среды меняется скачкообразно, в соответствии с этим процесс разбивается на три стадии (рис. 2.14):
1)до момента t = t1 :Tc (t ) = Tc1 =const;
2)при t1 < t < t2 :Tc (t ) = TП = const;
3)начиная с t = t2 до полного охлаждения пакета Tc (t ) = Tc1 = const.
Для указанных температур должно соблюдаться неравенство Tc1 < Tg2 < Tg1 < TП , т.е. Tc1 и TП должны находиться за пределами ин-
тервала стеклования. Данная задача описывает образование остаточных напряжений в изделиях из стеклующихся материалов при их остывании с последующим подогревом на временном промежутке t1 < t < t2 .
Рис. 2.13. Расчетная схема задачи |
Рис. 2.14. Режим изменения |
о совместном деформировании пакета |
температуры среды в задаче |
стеклующихся стержней |
о пакете стержней |
83
Решение тепловой задачи велось методом конечных разностей в предположении, что теплообмен с окружающей средой по боковым граням отсутствует. Постановка задачи имеет вид
|
|
|
ρc |
∂T = λ∂2T , t (0,t |
k |
], x |
(0, H ), |
||||
|
|
|
|
∂t |
∂x2 |
|
|
|
|
|
|
|
|
|
|
|
T (x,0) = TП, x [0, H ], |
|
|||||
λ |
∂T (x,t ) |
|
= αT |
(T (0,t ) − Tc (t )), |
∂T (x,t ) |
|
|
= 0, t (0,tk ], |
|||
|
|
||||||||||
∂x |
|
|
∂x |
|
|||||||
|
|
x = 0 |
|
|
|
|
|
x = H |
|||
|
|
|
|
|
|
|
|
|
|
||
где λ, c, ρ – теплопроводность, теплоемкость и плотность материала соответственно; H = nh, h – толщина одного стержня; αT – коэф-
фициент теплоотдачи.
Напряжения определялись по известному полю температур. Временной интервал разбивался на Nt шагов по времени. В каждый из этих моментов решалась система уравнений, содержащая физические соотношения в виде интегральной суммы и уравнение равновесия:
σi (t j ) = E1 (Ti (t j ))+ E2 (Ti (t j ))N (Ti (t j − 1 )) ×
|
|
|
j − 1 |
|
|
|
|
|
× ε(t j )− εT (t j )− |
|
С |
N (Ti (tm )) , |
|||||
ε |
|
(tm ) − εT (tm ) |
||||||
|
|
|
m = 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
i = |
|
; |
|
σi (t j ) = 0. |
|
||
|
1,n |
|
|
|||||
i = 1
Индекс «С» обозначает «замороженные» при стекловании деформации.
Степень стеклования описывается формулой (2.8). В расчетах
принимались следующие значения констант: λ = 0,19 Вт/м/К;
С= 1000 Дж/кг/К; ρ = 1600 кг/м3; αT = 500 Вт/м2/К; n = 15; H = 0,1 м;
TП = 170 °C; Tc1 = 20 °C. Механические характеристики ЭДТ-10 и па-
раметры кинетики взяты из разд. 2.5. Переход к модели И.И. Бугакова осуществлялся путем сужения интервала стеклования до нуля
84
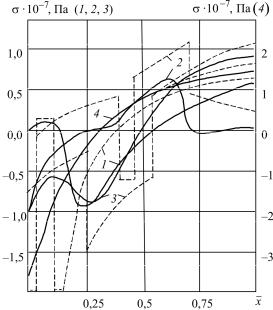
Рис. 2.15. Остаточные напряжения в пакете стержней после подогрева и остывания: 1 – t1 = 2500 с, t2 = 200 с;
2 – t1 = 2500 с, t2 = 400 с; 3 – t1 = 2000 с, t2 = 200 с;
4 – охлаждение без нагрева; сплошная линия – модель (2.5); штриховая линия – модель Бугакова
( γL = 0 в соотношениях (2.8)). На рис. 2.15 приведены кривые распределения остаточных напряжений в стержнях для различных сочетаний времен t1, t2 , рассчитанных по моделям (2.5) и (2.35). Анализ полученных результатов показывает, что повторный подогрев приводит к значительному снижению уровня остаточного напряженнодеформированного состояния. При простом охлаждении (t1 = t2 ) разница в расчетах по обеим моделям не превышает 25 %. Более существенные различия (до 75 %) возникают в разных вариантах повторного подогрева. Приведенный пример показывает, что использование упрощенных определяющих соотношений И.И. Бугакова (2.35)
85

дает хорошее качественное совпадение результатов расчета и допустимо в случаях, когда необходимо исследовать общие закономерности и эффекты при стекловании. Для прочностных расчетов, требующих точного количественного описания, модель (2.35) следует применять с осторожностью.
2.7.3. Реологическая модель А.П. Александрова – Ю.С. Лазуркина – Г.И. Гуревича
Наиболее подробный анализ данной модели [114] (называемой также обобщенным нелинейным уравнением Дж. Максвелла) применительно к эпоксидным смолам и простейшим конструкциям из них приведен в работах Р.А. Турусова [135] и В.Ф. Бабича [34]. Главной физической идеей, положенной в основу вывода уравнения связи, является постулат о направленности процесса перегруппировок молекул и перемещений их разнообразных комплексов в сторону стабильного расположения, при котором энергия совокупности молекул, образующих тело, имеет минимальное значение. Данное уравнение считается наиболее универсальным для описания поведения конденсированных сред, к которым относятся жидкости и твердые тела, и позволяет с высокой точностью описывать термомеханические свойства полимерных стеклующихся материалов. В одномерном варианте обобщенное нелинейное уравнение Дж. Максвелла имеет вид [72, 135]
σ = Eε,
где
nm
ε= ε− εT − εBS − εΠS ;
|
|
S = 1 |
|
|
S = 1 |
|
||
B |
|
2 3 |
E |
∞ |
B |
B ; |
(2.38) |
|
εS |
= |
σ− |
|
S |
εS |
|
ηS |
|
εΠS = 3 2σ
2σ ηΠS .
ηΠS .
86
Здесь ε – текущая деформация; εT – температурная деформация; εBS , εΠS – составляющая высокоэластической и пластической деформации для времени tS из спектра времен релаксации; ηBS , ηΠS –
соответствующие значения коэффициента релаксационной вязкости, являющиеся функциями давления, деформации объемного сжатия и температуры. Полная расшифровка функций, входящих в (2.38), не приводится в данной работе из-за громоздкости. Для полного количественного описания (2.38) требуется большое число экспериментов для определения неизотермической ползучести и релаксации [135]. Расчет напряженно-деформированного состояния конструкций с использованием (2.38) затруднен из-за нелинейности. На рис. 2.12 показаны теоретические кривые изменения напряжения в защемленном стержне, рассчитанные по (2.38) для ЭДТ-10 с учетом двух членов спектра времен высокоэластической деформации – старшего и младшего. Графики построены по данным работы [135] для различных скоростей изменения температуры. Соотношения (2.5), как видно из рисунка, не позволяют достаточно адекватно описывать экспериментально наблюдаемый гистерезис напряжений при повторных циклах нагрева–охлаждения образца, улавливаемый с помощью уравнения А.П. Александрова – Ю.С. Лазуркина – Г.И. Гуревича. В то же время модель (2.5) правильно отслеживает количественные и качественные эффекты, обусловленные изменением скорости охлаждения и нагрева. Наибольшие расхождения в расчетах по сравниваемым моделям должны наблюдаться при термостатировании в интервале стеклования из-за неучета релаксационных свойств полимера соотношениями (2.5). В переходных процессах (т.е. при непрерывном изменении температуры) в рассмотренном диапазоне скоростей нагрева–охлаждения соотношения (2.5) дают адекватное количественное описание термомеханического поведения стеклующихся полимеров. Для сравнения на том же рисунке приведен результат расчета напряжений в стержне по вязкоупругим соотношениям (2.31) (тонкая сплошная кривая). Как видно из рисунка, при этом наблюдается хорошее качественное и количественное совпадение с экспериментом.
87

2.8. МОДЕЛЬНАЯ ЗАДАЧА. АНАЛИЗ ЗАКОНОМЕРНОСТЕЙ
ФОРМИРОВАНИЯ ТЕХНОЛОГИЧЕСКИХ И ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В ПАКЕТЕ СТЕРЖНЕЙ
Предлагаемое аналитическое решение является хорошей иллюстрацией для понимания механизма формирования полей технологических и остаточных напряжений в изделиях из стеклующихся полимеров при неравномерном охлаждении с использованием описанной физической модели.
|
|
|
|
|
|
|
|
|
|
Рассмотрим напряжен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но-деформированное состо- |
x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
яние одномерной конструк- |
||
|
H |
|
|
|
|
|
|
|
|
ции, расчетная схема кото- |
|
|
|
|
|
|
|
|
|
|
рой показана на рис. 2.16. |
|
|
|
|
|
|
|
|
|
|
Расчетная область представ- |
|
|
|
|
|
|
|
|
|
|
ляет собой пакет бесконеч- |
|
|
l = 1 |
|
|
|
|
|
ε(t) |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
ного числа неравномерно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
охлаждаемых, совместно деформирующихся стержней из одного материала и одинакового поперечного сечения. Предпо-
лагается, что механическое взаимодействие между ними в направлении x (см. рис. 2.16) отсутствует, в то время как нестационарная температура меняется именно по этой координате. Представленная схема может служить модельным представлением сплошной полосы без поперечных связей, стеклующейся в неоднородном температурном поле.
Для получения аналитического решения используются следующие упрощающие гипотезы.
1. Деформация всех стержней ε(t) одинакова и известна. В начальный момент времени конструкция находится в естественном состоянии, т.е. ε(0) = 0 .
2. Координатно-временная функция температуры задается выражением
88
T (x,t) = T1 − (T1 − T0 )e− a( x)t , |
(2.39) |
где T1 – конечная температура (аналог температуры окружающей |
|
среды), T1 = T (x,∞) < Tg ; T0 – начальная температура |
пакета, |
T0 = T (x,0) > Tg ; |
|
a(x) = a1 + a2 x |
(2.40) |
является линейной координатной функцией скорости охлаждения. Положительность коэффициентов a1, a2 означает, например, что
медленнее остальных охлаждается слой с координатой x = 0 .
3. Модули материала стержней в высокоэластическом E1 и стеклообразном E2 состояниях, температура стеклования Tg и коэффици-
ент температурного расширения α не зависят от температуры.
4. Стеклование происходит мгновенно при T (x,t) = Tg , следова-
тельно, температурная зависимость степени стеклования может быть описана функцией Хевисайда
|
0, |
T (x,t) > T , |
|
N (x,t) = h(Tg |
|
g |
(2.41) |
− T (x,t)) = |
T (x,t) ≤ Tg . |
||
|
1, |
|
|
|
|
|
|
Формула (2.41) является частным случаем распределения Лап-
ласа (2.8) при γL → 0, Tg = const .
С учетом введенных предположений напряжения в пакете стержней (см. модель (2.6)) будут изменяться по закону
σ(x,t ) = (E1 + E2 N (x,t))(ε(t) − εT (x,t)) −
T ( x,t )
−E2 (ε(τ) − εT (x, τ)) dN (T (x, τ)),
T0
где εT (x,t) – температурная деформация, εT (x,t) = α(T (x,t) − T0 ) . Интегрирование с учетом гипотезы 4 (формула (2.41)) дает
σ(x,t ) = E1[ε(t) − εT (x,t)] − |
|
−E2 N (x,t)[(ε(t) − εT (x,t)) − (ε(tg (x)) − εT (x,tg (x)))], |
(2.42) |
89
где tg (x) – время достижения температуры стеклования в слое с координатой x. Его можно определить по формуле (2.39)
|
|
|
Tg |
= T1 − (T1 − T0 )e− a( x)tg , |
||
откуда tg |
(x) = |
1 |
T1 |
− Tg |
|
|
|
ln |
|
|
. |
||
−a(x) |
|
− T0 |
||||
|
|
T1 |
|
|||
В соответствии с гипотезой 3 температурная деформация в момент достижения температуры стеклования во всех слоях одинакова и равна
εT (x,tg (x)) ≡ εTg = α(Tg − T0 ) .
После приведения подобных соотношение (2.42) преобразуется к виду
σ(x,t ) = [E1 + E2 N (x,t)][ε(t) − εT (x,t)] − |
|
−E2 N (x,t)[ε(tg (x)) − εTg ]. |
(2.43) |
В формуле (2.43) остается неопределенной зависимость деформации пакета от времени ε(t) . Анализ выражения (2.43) показывает, что при заданном законе изменения температуры (2.39), (2.40) и принятой гипотезе о постоянстве температуры стеклования для образования остаточных напряжений необходимо, чтобы ε(t) ≠ 0 . В самом деле, наличие остаточных напряжений возможно лишь в случае, когда напряженное состояние при полном охлаждении до температуры T1 всех слоев пакета неравномерно. При нулевой деформации, с учетом того что N (x,∞) = 1, напряжения во всех стержнях по (2.43) будут равны между собой
σ(x,∞ ) = −α(T1 − T0 )[E1 + E2 ] + εTg E2 ,
следовательно, остаточные напряжения будут отсутствовать.
90
