книги / Несущая способность конструкций в условиях теплосмен

IIIIσ = σxx σ yy σzz + 2σxy σ yz σxz − σxxσ2yz − σ yy σ2xz − σzz σ2xy .

Триинварианта тензора деформации вычисляютсяаналогично:

IIε = ε xx + ε yy + ε zz ;

IIIε = ε xx ε yy + ε yy εzz + ε xx ε zz − ε2xy − ε2yz − ε2xz ;

IIIIε = εxx ε yy εzz + 2εxy ε yz εxz − εxxε2yz − ε yy ε2xz − ε zz ε2xy .

С использованием вторых инвариантов получают интенсивность напряжения σi и интенсивность деформации εi:

Величины интенсивностей напряжения и деформации используются как обобщающие характеристики напряженно-деформиро- ванного состояния материала и замещающие (в некотором смысле) тензоры напряжения и деформации – эквивалентные, расчетные напряжения и деформации.

52

6. ФИЗИЧЕСКИЕ МОДЕЛИ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА

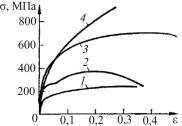
Диаграммы зависимости напряжения от деформации, изображенные на рис. 6.1, показывают поведение различных материалов при растяжении в процессе нагружения [17]. Когда образец материала разгружается, то есть когда нагрузка постепенно уменьшается до нуля, удлинение, которое возникло при нагружении, будет частично или полностью исчезать. Это свойство материала при разгрузке возвращаться к своим первоначальным форме и размерам называется

но. Примером могут служить начальные участки диаграмм зависимости напряжения σ от деформации ε, приведенные на рис. 6.1.

6.1.Зависимость между деформацией и напряжением

вупругом материале

Если материал ведет себя упруго и, кроме того, существует линейная зависимость между напряжением и деформацией, он называется линейно-упругим. Это важное свойство многих твердых материалов, таких как древесина, бетон, керамика, большинство металлов, пластмассы. Линейная зависимость между напряжением и де-

53

формацией при растяжении стержня может быть представлена простым соотношением, называемым законом Гука29:

где Е – коэффициент пропорциональности, известный как модуль упругости материала (модуль Юнга30). Модуль упругости представляет собою тангенс угла наклона диаграммы зависимости напряжения от деформации на линейно-упругом участке деформирования и различен для разных материалов. Некоторые характерные значения модуля упругости Е приведены в табл. 6.1. Из выражения (6.1) следует, что модуль упругости имеет ту же размерность, что и напряжение. Для большинства материалов модуль упругости при сжатии такой же, как и при растяжении.

29Гук Роберт (18.07.1635–03.03.1703) – английский ученый, один из основателей Лондонского королевского общества. С 1665 г. преподавал в Лондонском университете в должности профессора. Основные труды выполнены в области физики и астрономии. Начал разработку основ математической теории упругости.

30Юнг Томас (1773–1829) – английский ученый, один из основоположников волновой теории света, сформулировал принцип интерференции, ввел понятие модуля упругости, названного его именем. Наибольший вклад внес в акустику, астрономию, расшифровку египетских иероглифов.

54

Когда стержень нагружается простым растяжением, продольные (осевые) напряжение и деформация определяются выражениями (3.1) и (4.1). Присоединяя к этим выражениям закон Гука (6.1), можно получить следующее выражение для удлинения стержня:

Из этого выражения следует, что удлинение стержня из ли- нейно-упругого материала прямо пропорционально нагрузке Р и его длине L, обратно пропорционально модулю упругости E и площади поперечного сечения F.

Податливость стержня определяется как удлинение, вызванное единичной нагрузкой, P = 1; из выражения (6.2) следует, что податливость равна LEF .

Величина EFL , обратная податливости, называется жестко-

стью стержня при растяжении или сжатии. Жесткость стержня можно определить как силу, необходимую для удлинения стержня на величину δ = 1. Податливость и жесткость играют важную роль при анализе конструкций различного вида.

6.2. Продольная и поперечная деформации

Эксперименты показывают, что при действии на стержень растягивающей нагрузки осевое удлинение сопровождается уменьшением размера и площади поперечного сечения, то есть увеличение длины стержня сопровождается уменьшением его ширины и высоты (см. рис. 6.1). Отношение деформации в поперечном направлении к продольной деформации для упругого материала постоянно; оно называется коэффициентом Пуассона31 и обозначается греческой буквой ν32. Таким образом, коэффициент Пуассона

31Пуассон Симеон Дени (21.06.1781–25.04.1840) – французский математик, механик и физик, член Парижской академии наук, иностранный член Лондонского королевского общества, иностранный почетный член Петербургской академии наук.

32Греческая буква «ню».

55

ν = ПродольнаяПоперечная деформациядеформация.

Для изотропных материалов, т.е. имеющих одинаковые упругие свойства во всех направлениях, в большинстве случаев ν = 0,25. Эксперименты показывают, что коэффициент Пуассона для металлов принимает значения от 0,25 до 0,35.

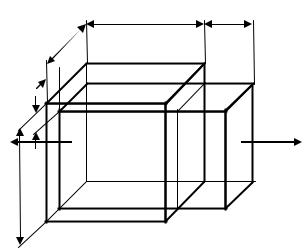
Если для материала известны коэффициент Пуассона и модуль упругости, то можно подсчитать изменение объема стержня, например, при растяжении. На рис. 6.2 показано изменение объема кубического элемента материала с ребром единичной длины, выделенного из растягиваемого образца.

1 ε

1

νε

νε

1

Рис. 6.2. Изменение объема при растяжении куба с ребром единичной длины

Первоначальный элемент берется в виде куба, длина ребра которого равна 1. Направление действия растягивающего усилия показано на рисунке. Относительное удлинение ребра такого куба в направлении нагружения ε = σE , относительное укорочение ребер

куба в обоих поперечных направлениях составляет νε . Таким образом, площадь поперечного сечения первоначального куба уменьша-

56

ется до значения (1 − νε1)2 , а объем увеличивается до значения

(1 + ε1)(1 − νε1)2 .

Если раскрыть скобки в полученном выражении и опустить слагаемые, в которые входят квадраты и куб малой величины ε, то это отношение упростится и примет вид (1 + ε − 2νε ). Изменение

объема равно разности между окончательным и первоначальным объемами, то есть 33V = ε (1 − 2ν ). Эта величина называется отно-

сительным изменением объема и может быть представлена в виде

чальному объему V. Это выражение можно использовать для вычисления изменения объема растягиваемого стержня, если известны осевая деформация ε и коэффициент Пуассона ν.

Поскольку материалы не могут уменьшать свой объем при растяжении, из выражения (6.3) можно сделать вывод, что коэффициент Пуассона ν должен быть всегда меньше 0,5. Резина и парафин представляют собой два вида материалов, которые практически не меняют объема при растяжении, поэтому для указанных материалов, как показывают эксперименты, коэффициент ν приближается к своему предельному значению 0,5. С другой стороны, пробка – материал, для которого коэффициент ν практически равен 0; для бетона ν примерно равен 0,1.

Приведенное выше обсуждение уменьшения поперечного размера, происходящего при растяжении, может быть распространено также и на случай продольного сжатия, с учетом того, что сжатие сопровождается увеличением поперечного размера. Для практических целей числовое значение коэффициента Пуассона при сжатии и при растяжении материала считается одинаковым.

33 Греческая прописная буква «дельта».

57

6.3. Обобщенный закон Гука

При сложном нагружении в случае упругого деформирования зависимость между компонентами тензоров деформации и механического напряжения подчиняется обобщенному закону Гука:

Возможна запись закона Гука в форме зависимости компонент тензора деформации от компонент тензора напряжения:

Связь (6.4) компонент тензора напряжения и тензора деформации с учетом введенных обозначений (5.1) и (5.5) целесообразно представить в матричном виде

{σ} = [D]{ε}.

В развернутой записи это соотношение представляется в виде

58

6.4. Пластичность материалов

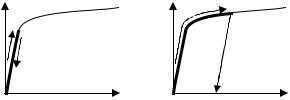
Если после снятия приложенной нагрузки стержень (конструкция) полностью восстанавливает свою первоначальную форму, то его называют идеально упругим (участок деформирования на рис. 6.3, а), если же частично – то частично упругим (неупругим) деформированием (участок деформирования на рис. 6.3, б). В последнем случае удлинение, которое остается в стержне после того, как снята нагрузка, называется остаточной деформацией.

При проведении испытания материала на растяжение нагрузка доводится до некоторой заданной величины и затем снимается. Если при этом не обнаружится остаточной деформации, то есть деформация стержня обратится в нуль, то материал является упругим вплоть до напряжения, соответствующего выбранной величине нагрузки

(см. рис. 6.3, а).

Рис. 6.3. Диаграммы механического нагружения призматического стержня в областях упругого (а) и неупругого (б) деформирования материала

Подобные процессы нагружения и разгрузки могут повторяться для последовательно увеличивающихся значений нагрузки. Наконец, будет достигнуто такое напряжение, когда при разгрузке стержень не вернется в исходное состояние, при этом в стержне появится остаточная деформация (см. рис. 6.3, б).

На диаграмме упругопластического растяжения призматического стержня (рис. 6.4) имеется ряд точек, характерных для большинства конструкционных и инструментальных материалов и сталей.

60