Турищев Л.С. (сост.) Строительная механика. Часть 2. Статически неопределимые системы. ПГУ, 2009

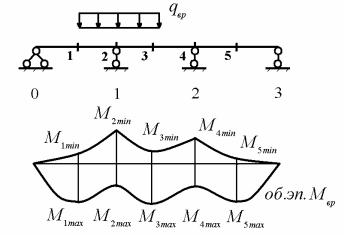
и, следовательно, опасным положением временной нагрузки для этого сечения является ее одновременное расположение в первом и третьем пролетах.

Минимальные значения изгибающих моментов в каждом расчетном сечении получают сложением соответствующих отрицательных величин моментов. Например, для второго расчетного сечения получим

M2 min M21 M22

и, следовательно, опасным положением временной нагрузки для этого сечения является одновременное нагружение первого и третьего пролетов.

Откладывая в каждом расчетном сечении, найденные для него максимальные и минимальные значения изгибающих моментов и соединяя, соответственно, вершины положительных и отрицательных ординат, получим объемлющую эпюру изгибающих моментов (рис. 10.32).

Рис. 10.32

10.5. Резюме

Неразрезная балка является внешне статически неопределимой конструкцией, используемой для перекрытия пролетов в сооружениях различного назначения.

Расчет неразрезной балки обычно производится методом сил с использованием основной системы в виде многопролетной шарнирной балки, получаемой введением шарниров во все промежуточные опорные сечения неразрезной балки.

Канонические уравнения метода сил для такого варианта основной системы неразрезной балки называются уравнениями трех моментов и они имеют вид трехдиагональной ленточной системы линейных неоднородных алгебраических уравнений.

91

Распределение изгибающих моментов в незагруженных пролетах неразрезной балки, при условии расположения нагрузки по отношению к ним с одной стороны, подчиняется определенным закономерностям. Эти закономерности описываются фокальнымисвойствами неразрезной балки.

Использование фокальных свойств позволяет находить изгибающие моменты в неразрезной балке без составления и решения уравнений трех моментов. Такой метод нахождения изгибающих моментов называется методом моментных фокусных отношений.

Расчет неразрезных балок на действие временной нагрузки связан с построением объемлющих эпюр внутренних усилий. Существует два способа построения таких эпюр – точный и упрощенный.

10.6. Материалы для самоконтроля

Проверьте, как Вы усвоили следующие понятия, определения, алгоритмы и формулы:

–неразрезная балка;

–типы неразрезных балок;

–нумерация опор и пролётов;

–степень статической неопределимости;

–основные системы метода сил для неразрезных балок;

–канонические уравнения метода сил;

–уравнения трёх моментов для нагрузки;

–уравнения трёх моментов для осадки опор;

–решение системы уравнений трёх моментов;

–формулы для определения окончательных изгибающих моментов

ипоперечных сил от нагрузки;

–формулы для определения окончательных изгибающих моментов

ипоперечных силот осадки опор;

–формулу для определения опорной реакции на произвольной опоре неразрезной балки;

–фокальные свойства;

–моментные фокусы;

–формулы для вычисления моментных фокусных отношений;

–интервал изменения моментных фокусных отношений;

–объемлющая эпюра;

–способы построения объемлющих эпюр.

92

Проверьте, как Вы умеете при расчетенеразрезных балок:

–нумеровать опоры и пролёты;

–образовывать основную систему;

–составлять и решать уравнения трёх моментов;

–строить эпюры окончательных изгибающих моментов и поперечных сил;

–определять опорные реакции;

–строить эпюры окончательных изгибающих моментов и поперечных сил методом моментных фокусных отношений.

Проверьте, можете ли Вы вывести:

–уравнения трёх моментов при действии нагрузки;

–уравнения трёх моментов при действии осадки опор;

–формулы для вычисления фокусных отношений;

–формулы для расчёта неразрезной балки методом моментных фокусных отношений.

Проверьте, можете ли Вы обосновать:

–фокальные свойства неразрезной балки.

93

М-11. МЕТОД ПЕРЕМЕЩЕНИЙ

11.0. Введение в модуль

Основными целями модуля являются:

рассмотрение понятия степени кинематической неопределимости;

получение формул для определения внутренних усилий в произвольной плоской статически неопределимой раме;

рассмотрение особенностей определения внутренних усилий с учетом симметрии плоской статически неопределимой рамы;

рассмотрение особенностей применения метода перемещений к плоским статически неопределимым рамам с ригелями повышенной изгибной жесткости;

рассмотрение особенностей определения внутренних усилий в плоских статически неопределимых несвободных рамах при действии узловой нагрузки.

Структураизучаемогомодуля включаетследующие учебныеэлементы: 1. Расчет плоских статически неопределимых рам методом переме-

щений.

2. Использование свойств симметрии при расчете рам методом перемещений.

3. Особенности применения метода перемещений к рамам с ригелями повышенной изгибной жесткости.

4. Особенности определения внутренних усилий в несвободных рамах при действии узловой нагрузки.

При изучении учебных элементов рекомендуется использование сле-

дующей литературы: [1, c.391 – 448]; [3, c.265 – 302]; [4, c.365 – 378]; [5, c. 372 – 404].

11.1. Расчет плоских статически неопределимых рам методом перемещений

11.1.1. Суть метода и его допущения

Расчет статически неопределимой рамы методом сил начинается с определения ее степени статической неопределимости, которая равняется

94

числу лишних связей в системе, и нахождения основных неизвестных, которыми являются внутренние усилия, возникающие в этих связях. После этого легко определяются и остальные внутренние усилия. Зная же внутренние усилия, можно найти перемещения в любом месте рамной системы.

Однако наряду с порядком расчета рамы, когда сначала определяются внутренние усилия, а затем находятся перемещения, возможен и иной порядок определения этих величин. Если для некоторой рамной конструкции каким-либо образом найти ее узловые перемещения (линейные и угловые), то после этого нетрудно будет найти и все внутренние усилия в стержнях системы. Такой порядок расчета стержневой системы и составляет сущность метода перемещения. Узловые перемещения, подлежащие первоочередному определению, являются основными неизвестными ме-

тода перемещений, а их общее число и называется степенью кинемати-

ческой неопределимости n. Сама же стержневая система считается кинематически неопределимой.

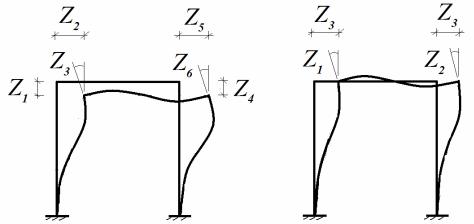
При определении степени кинематической неопределимости в рамах вводятся два допущения. Во-первых, пренебрегают продольными и поперечными деформациями стержней, поскольку при определении перемещений в рамных системах, как правило, учитываются только деформации изгиба. И, во-вторых, ввиду малости перемещений в линейно деформируемых системах, пренебрегают сближением концов изгибаемых стержней. Введение указанных допущений позволяет не учитывать при расчете второстепенные перемещения и, следовательно, уменьшать степень кинематической неопределимости.

Рис. 11.1

Пример, приведенный на рис. 11.1, показывает, что, с учетом принятых допущений, степень кинематической неопределимости рамы уменьшилась в два раза.

95

Степень кинематической неопределимости произвольной плоской рамы определяется по формуле

n n1 n2 ,

где n1 – число неизвестных угловых перемещений узлов рамы, n2 – число

неизвестных линейных перемещений узлов рамы, которое характеризует степень линейной подвижности рамы.

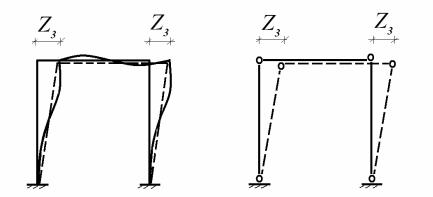
Число неизвестных угловых перемещений n1 равняется числу жестких узлов рамы. Для определения степени линейной подвижности рамы n2 во все

жесткие узлы рамы вводятся шарниры. Число степеней свободы, полученной шарнирно стержневой системы, совпадает со степенью линейной подвижности рамы. Следовательно, для рамы, показанной на рис.11.2, n2 1.

Рис. 11.2

Рамы, у которых могут возникать линейные перемещения узлов только за счет изгибных деформаций ее стержней n2 0 , принято называть свободными рамами. Рамы, у которых такие перемещения отсутствуют n2 0 , называются несвободными рамами.

11.1.2. Постановка задачи

Задана произвольная плоская статически и кинематически неопределимая рама (рис. 11.3).

Степень кинематической неопределимости рамы характеризуется величинами n, n1 0, n2 0, которые определяются в соответствии с неизвестными узловыми перемещениями Z1 ,...,Zn . Для рамы считаются из-

вестными геометрические размеры расчетной схемы, геометрические характеристики поперечных сечений стержней и их конструкционный материал. В пределах каждого стержня геометрические характеристики поперечного сечения считаются постоянными. Способность произвольного

96

стержня рамы сопротивляться изгибным деформациям будем описывать величиной погонной жесткости

Рис. 11.3

На раму действуют произвольная нагрузка. Заданная конструкция считается линейно деформируемой системой.

11.1.3. Основная система и канонические уравнения

В основе расчета рам методом перемещений лежит переход от заданной кинематически неопределимой системы к расчету эквивалентной кинематически определимой системе. Эквивалентность двух систем должна состоять в одинаковости перемещений (кинематическая эквивалентность метода перемещений) и одинаковости внутренних усилий (стати-

ческая эквивалентность метода перемещений). Такая эквивалентная система и называется основной системой метода перемещений.

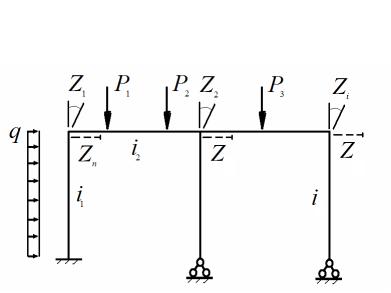
Для получения основной системы из заданной на узлы рамы накладываются дополнительные связи, которые исключают возможность возникновения угловых и линейных перемещений ее узлов (рис. 11.4).

Для исключения угловых перемещений на все жесткие узлы накладываются связи, исключающие их повороты. Такие связи для краткости будем называть «шайбами» и изображать в виде квадрата, окаймляющего жесткий узел. Для исключения линейных перемещений на узлы по направлению этих перемещений накладываются стержни. Преобразованная таким образом система состоит из отдельных статически неопределимых балок, в

97

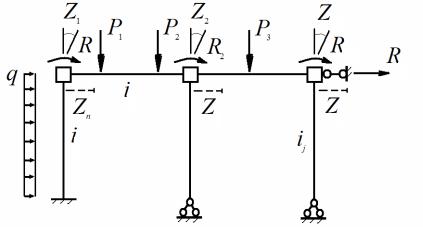
ней отсутствуют все узловые перемещения и, следовательно, она является

кинематически определимой системой.

Рис. 11.4

Кинематическая эквивалентность полученной кинематически опре-

делимой системы заданной системе достигается приложением к ней в качестве дополнительных внешних воздействий неизвестных узловых перемещений Z1 ,...,Zn (рис. 11.4). При дальнейшем расчете эти перемещения подлежат

первоочередному определению и поэтому они называются основными неизвестными метода перемещений. И, поскольку, основные неизвестные являются перемещениями, то они имеют кинематическую природу.

Для достижения статической эквивалентности двух систем вводятся условия обращения в ноль реакций (рис. 11.4)

возникающих в кинематически определимой системе в наложенных связях по направлению основных неизвестных. И так как эти реакции порождаются основными неизвестными и заданной внешней нагрузкой, то они являются функциям этих величин и условия (11.1) можно записать в следующем виде

R1 Z1,...,Zn , P 0,

.............................. (11.2) Rn Z1,...,Zn , P 0.

Поскольку заданная стержневая конструкция считается линейно деформируемой системой, то дополнительные условия (11.2), согласно принципу суперпозиции, принимают вид

98

R1Z1 ... R1Zn R1P 0,

..................................... (11.3) RnZ1 ... RnZn RnP 0.

Входящие в (11.3) величины имеют следующий смысл: RiZ j i, j 1,...,n –

реакция в наложенной связи основной системы по направлению основного неизвестного № i, вызванная действием основного неизвестного Z j ;

RiP i 1,...,n – реакция в наложенной связи основной системы по на-

правлению основного неизвестного № i , вызванная действиемнагрузки. Так как изменения реакции RiZ j и основного неизвестного Z j свя-

где rij – единичная реакция в наложенной связи основной системы по направлению основного неизвестного № i от действия безразмерного перемещения Z j 1.

С учетом (11.4) соотношения (11.3) принимают вид уравнений

r11Z1 ... r1nZn R1P 0,

...................................... (11.5)

rn1Z1 ... rnnZn RnP 0.

Полученные уравнения (11.5) представляют собой систему неоднородных линейных алгебраических уравнений относительно основных неизвестных

Z1,...,Zn и называются каноническими уравнениями метода перемеще-

ний. Они имеют статическую природу, так как каждое такое уравнение выражает равенство нулю реакции в наложенной связи основной системы по направлению основного неизвестного, номер которого совпадает с номером соответствующего уравнения, от действия всех основных неизвестных и нагрузки.

Входящие в эти уравнения единичные реакции rij в качестве множи-

телей при основных неизвестных называются коэффициентами канони-

ческих уравнений метода перемещений. В зависимости от соотношений между индексами различают два вида таких коэффициентов. В случае если i j , то соответствующие коэффициенты называются главными коэф-

фициентами, и они удовлетворяют условию строгой положительности rii 0 i 1,...,n .

99

В случае если i j , то соответствующие коэффициенты называются побочными коэффициентами, и они удовлетворяют условию взаимности

Входящие в канонические уравнения реакции RiP i 1,...,n от дей-

ствия нагрузки называются свободными членами канонических уравнений метода перемещений.

11.1.4. Определение коэффициентов и свободных членов

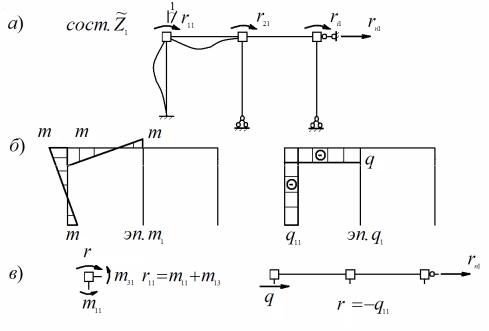
Для определения коэффициентов канонических уравнений метода перемещений нужно последовательно загрузить основную систему безраз-

мерными перемещениями Z j 1 j 1,...,n . Такие схемы нагружения счи-

таются единичными состояниями основной системы метода перемеще-

ний. Пример образования единичного состояния приведен на рис. 11.5, а.

21

состояния основной системы (рис. 11.5,б).

Для определения свободных членов канонических уравнений RiP i 1,...,n необходимо рассмотреть основную систему под действием

нагрузки и построить эпюры изгибающих моментов MP и поперечных сил QP . Такие эпюры MP , QP называются грузовыми, а соответствующая им схема нагружения считается грузовым состоянием основной системы.

100