Турищев Л.С. (сост.) Строительная механика. Часть 2. Статически неопределимые системы. ПГУ, 2009

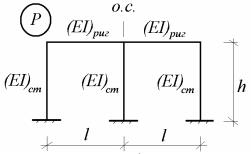
рассмотрим три единичных состояния и построим эпюры единичных изгибающих моментов (рис. 8.6, б). Однако в этом случае среди единичных эпюр появились эпюры, имеющие антисимметричное очертание (эп. m1) и симметричные очертания (эп. m2, m3). Это является следствием того, что три лишних связи были удалены в сечении, лежащем на оси симметрии, и основные неизвестные сами разделились на антисимметричные X1 и симметричные величины X2, X3 .

Поэтому все побочные коэффициенты, получаемые при перемножении эпюр симметричного и антисимметричного очертаний, будут тождественно равны нулю

12 21 13 31 0 .

В этом случае система канонических уравнений (8.25) распадается на две подсистемы уравнений

11X1 1P 0

Следовательно, второй вариант основной системы позволяет независимо найти антисимметричное основное неизвестное и симметричные основные неизвестные.

Таким образом, сохранение свойств симметрии при образовании основной системы и разделение неизвестных на симметричные и антисимметричные величины позволяет получить рациональную основную систему метода сил. Симметричные статически неопределимые стержневые конструкции, для которых удается удалить все лишние связи в сечениях, принадлежащих оси симметрии и, как следствие этого, получить автоматическое разделение основных неизвестных метода сил на симметричные и антисимметричные величины, будем называть симметричными системами частного вида.

8.3.3. Расчет симметричных систем общего вида

Рассмотрим одноэтажную двух пролетную раму (рис. 8.7), удовлетворяющую все признакам симметрии и обладающую осью симметрии.

На раму действует произвольная нагрузка, показанная на рис. 8.7 услов-

ным буквенным обозначением P.

Рис. 8.7

41

Рассматриваемая рама шесть раз статически неопределимая система

и все лишние связи содержатся в опорных закреплениях. Расчет такой рамы, при любой схеме удаления лишних связей для получения основной системы метода сил, связан с составлением и решением шести канонических уравнений

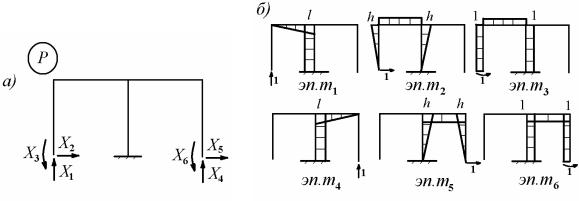
Образуем основную систему, соблюдая признаки симметрии стержневой конструкции. Для этого удалим крайние опорные закрепления (рис.

8.8, а).

Рис. 8.8

Однако если рассмотреть все единичные состояния (рис. 8.8, б), то из построенных единичных эпюр изгибающих моментов, очевидно, что ни один из побочных коэффициентов не равен нулю

Следовательно, сохранение свойств симметрии геометрических размеров, схем узловых соединений и жесткостных характеристик не позволило получить для рассматриваемой симметричной рамы более общего вида рациональную основную систему метода сил, как это произошло в частном случае. Причиной этого является отсутствие автоматического разделения основных неизвестных метода сил на симметричные и антисимметричные величины.

42

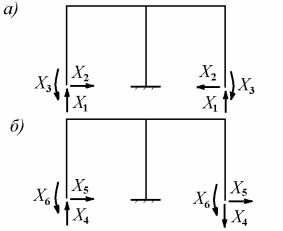
Поэтому для симметричных систем общего вида применяют группировку однотипных основных неизвестных и искусственное выделение симметричных и антисимметричных составляющих. Такое разделение для рассматриваемой рамы показано нарис. 8.9.

В этом случае единичные эпюры изгибающих моментов m1, m2,m3 , связанные с симметричными основными неизвестными (рис. 8.9, а), будут иметь симметричные очертания. Единичные эпюры изгибающих моментов m4, m5,m6 , связанные с антисимметрич-

ческих уравнений (8.26), получаемые при перемножении симметричных единичных эпюр с антисимметричными и наоборот, тождественно равны нулю

С учетом (8.28), система канонических уравнений (8.27) распадается на две независимые подсистемы уравнений. Первая подсистема уравнений содержит только симметричные основные неизвестные (рис. 8.9, а)

11X1 12 X2 13X3 1P 0

21X1 22 X2 23 X3 2P 0

31X1 32 X2 33 X3 3P 0

а вторая – только антисимметричные основные неизвестные (рис. 8.9, б)

44 X4 45 X5 46 X6 4P 0

54 X4 55 X5 56 X6 5P 0

64 X4 65 X5 66 X6 6P 0

Таким образом, группировка основных неизвестных и искусственное выделение симметричных и антисимметричных основных неизвестных позволяет получить рациональную основную систему в общем случае. Симметричную стержневую систему, в которой для образования рациональной основной системы требуется применять группировку основных неизвестных, будем называть симметричной системой общего вида.

43

8.3.4. Особенности расчета симметричных систем на симметричные и антисимметричные нагрузки

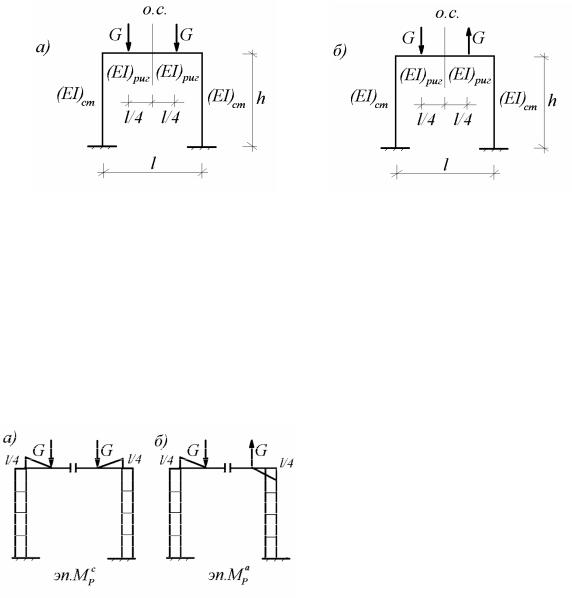
Рассмотрим особенности такого расчета на примере симметричной одноэтажной однопролетной рамы, загруженной в одном случае симметричной нагрузкой (рис. 8.10, а) и в другом случае – антисимметричной нагрузкой (рис. 8.10, б).

Рис. 8.10

Рациональная основная система метода сил показана на рис. 8.6, а и ее выбор не зависит от схемы нагружения. Поэтому, как в случае симметричной схемы нагружения, так и в случае антисимметричной схемы нагружения для расчета рамы будет использоваться система канонических уравнений (8.26).

Для определения свободных членов канонических уравнений рассмотрим грузовые состояния основной системы и построим грузовые эпюры из-

гибающих моментов (рис.8.11). При действии симметричной

нагрузки грузовая эпюра изгибающих моментов имеет симметричное очертание (рис. 8.11, а). Поэтому свободный член 1P , по-

Два других свободных члена 2P и 3P , получаемые при перемножении при перемножении симметричной грузовой эпюры MP (рис. 8.11, а) с

44

единичными эпюрами m2 , m3 , имеющими симметричное очертание

(рис. 8.6, в), будут отличными от нуля

2P 0, 3P 0

Тогда решая систему канонических уравнений (8.26), с учетом (8.29), получим, что антисимметричное основное неизвестное X1 будет равно

X1 0 .

Обобщая полученный результат, можно сделать первый вывод, связанный с особенностями расчета методом сил симметричных стержневых систем. При расчете таких систем на действие симметричной нагрузки все антисимметричные основные неизвестные метода сил тождественно равны нулю.

При действии антисимметричной нагрузки грузовая эпюра изгибающих моментов имеет антисимметричное очертание (рис. 8.11, б). Поэтому свободные члены 2P и 3P , получаемые при перемножении антисиммет-

ричной грузовой эпюры MP с единичными эпюрамиm2 , m3 ,, имеющими симметричное очертание (рис.8.6.в), будут тождественно равны нулю

X2 0, X3 0.

Обобщая полученный результат, можно сделать второй вывод, связанный с особенностями расчета методом сил симметричных стержневых систем. При расчете таких систем на действие антисимметричной нагрузки все симметричные основные неизвестные метода сил тождественно равны нулю.

8.3.4. Общий порядок расчета методом сил симметричной стержневой системы общего вида на действие произвольной нагрузки

Расчет методом сил произвольной n раз статически неопределимой симметричной стержневой системы включает следующие этапы:

1.Раскладываем нагрузку заданного состояния на симметричную и антисимметричную составляющие.

2.Образуем симметричную основную систему метода сил, используя для этого в общем случае прием группировки однотипных основных неиз-

вестных и искусственное выделение симметричных Xi i 1,...,k и антисимметричных основных неизвестных X j j k 1,...,n .

3. Составляем раздельно канонические уравнения метода сил для симметричного и антисимметричного состояний основной системы.

45

4. Решаем канонические уравнения и находим симметричные основные неизвестные Xi i 1,...,k и антисимметричные основные неизвест-

ные X j j k 1,...,n .

5. Находим внутренние усилия для заданной системы от действия симметричной составляющей нагрузки

M c m1X1 ... mk Xk M Pc Qc q1X1 ... qk Xk QPc N c n1X1 ... nk Xk NPc

6. Находим внутренние усилия для заданной системы от действия антисимметричной составляющей нагрузки

7. Находим внутренние усилия для заданной системы от действующей на нее произвольной нагрузки

MM c M a

Q Qc Qa

NN c N a

8.4.Матричная форма расчета методом сил плоских статически неопределимых стержневых конструкций

8.4.1. Постановка задачи

Задана плоская n раз статически неопределимая стержневая конструкция, на которую действует произвольная нагрузка. Для применения аппарата матричной алгебры к расчету заданной системы методом сил необходимо осуществить дискретизацию расчетной схемы стержневой конструкции и действующей на нее нагрузки.

Будем считать, что в результате дискретизации расчетной схемы конструкции она разбита на s отдельных элементов, соединенных между собой и с основанием в f узлах, и в ней выделено r расчетных сечений. В результате дискретизации нагрузки получена статически эквивалентная система сосредоточенных сил и сформирован вектор нагрузки

G G1Gf

46

или матрица нагрузок

вслучае действия сочетания k нагрузок.

Вдискретизированной заданной системе удаляем n лишних связей, получаем основную систему метода сил и записываем для нее канонические уравнения в матричной форме

Дальнейшее решение задачи заключается в отыскании вектора основных неизвестных метода сил

X1

X ,Xn

а также векторов внутренних усилий заданной системы

или матриц таких усилий в случае действия сочетания k нагрузок

8.4.2. Вывод матричной формулы для нахождения вектора основных неизвестных

Решение канонических уравнений (8.31) имеет вид

Таким образом, для получения матричной формулы, позволяющей получить вектор основных неизвестных, необходимо сформировать матрицу коэффициентов канонических уравнений и вектор свободных членов от действия нагрузки.

47

Для формирования матрицы A

используем матричный вариант формулы Максвелла – Мора при определении единичных перемещений с учетом только изгибных деформаций

транспонированный вектор изгибающих моментов i – того единичного состояния

m10j m0j mrj0

вектор изгибающих моментов j-того единичного состоянияи

матрица податливости изгибным деформациям разрозненных элементов основной системы.

Подставляя (8.34) в (8.33) и используя представление квадратной матрицы в виде произведения столбца на строку, образованных из ее элементов, получим формулу для формирования матрицы А

матрица влияния изгибающих моментов основной системы, связанная с действием основных неизвестных.

48

Вслучае учета продольных деформаций при формировании матрицы

Аформула (8.35) приобретает вид

где BN – матрица податливости продольным деформациям разрозненных элементов основной системы; L0n – матрица влияния продольных сил основной системы, связанная с действием основных неизвестных.

Для формирования вектора P

используем матричный вариант формулы Максвелла–Мора при определении перемещений от действия нагрузки с учетом только изгибных деформаций

Здесь

M 0 MP0 1PMrP0

вектор изгибающих моментов грузового состояния основной системы.

Подставляя (8.38) в (8.37), получим формулу для формирования вектора P

В случае учета продольных деформаций при формировании вектора P

Формула (8.39) приобретает вид

С учетом полученных формул для формирования матрицы коэффициентов канонических уравнений и вектора свободных членов от действия нагрузки формула (8.32) для определения вектора основных неизвестных с учетом только изгибных деформаций принимает вид

49

В случае учета и продольных деформаций эта формула имеет вид

8.4.3. Вывод матричных формул для определения внутренних усилий заданной системы

При использовании скалярной формы уравнений метода сил, возникающие в заданной системе изгибающие моменты от действия нагрузки, определяются по формуле

M MP0 m10 X1 ... mn0 Xn .

Применяя эту формулу к каждому расчетному сечению, получим ее матричный аналог

Так как заданная система является линейно деформируемой, представим входящий в (8.43) вектор изгибающих моментов грузового состояния в виде

матрица влияния изгибающих моментов основной системы, связанная с действием нагрузки.

Тогда формула (8.43), позволяющая определять изгибающие моменты в заданной системе от действия нагрузки, с учетом (8.41) и (8.44) принимает вид

50