
Турищев Л.С. (сост.) Строительная механика. Часть 2. Статически неопределимые системы. ПГУ, 2009
.pdfПроверьте, как Вы умеете при расчете статически неопределимых стержневых систем методом перемещений:
–определять степень кинематической неопределимости;
–изображать в заданной системе основные неизвестные;
–образовывать основную систему;
–учитывать различие жесткостных характеристик ригеля и стоек при образовании основной системы;
–составлять канонические уравнения;
–образовыватьединичныесостоянияистроитьединичныеэпюрыm, q;
–образовывать грузовое состояние и строить грузовые эпюры M, Q;
–находить коэффициенты и свободные члены канонических урав-
нений;
–использовать свойства симметрии;
Проверьте, можете ли Вы вывести:
–канонические уравнения и формулы для расчёта n-раз кинематически неопределимой стержневой системы методом перемещений на действие нагрузки.
Проверьте, можете ли Вы доказать:
–правомерность использования шарнирных узлов при расчёте ферм на действие узловой нагрузки.
111
М-12. ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
12.0. Введение в модуль
Основными целями модуля являются:
введение понятий конечного элемента и узла;
рассмотрение типов конечных элементов и их характеристик;
получение матриц жесткости одномерного конечного элемента.
получение матрицы жесткости конструкции;
описание общей схемы применения метода конечных элементов. Структураизучаемогомодуля включаетследующие учебныеэлементы: 1. Общие сведения о методе конечных элементов.
2. Расчет стержневых конструкций методом конечных элементов в
форме метода перемещений.
При изучении учебных элементов рекомендуется использование сле-
дующей литературы: [3, c. 435 – 493]; [5, c. 466 – 514].
12.1.Общие сведения о методе конечных элементов
12.1.1.Суть метода и его разновидности
Основная идея метода конечных элементов состоит в том, что рассчитываемая строительная конструкция заменяется совокупностью некоторых элементов, соединенных между собой и с основанием в конечном числе точек. Элементы, на которые разбивается строительная конструкция, называются конечными элементами, а точки их соединения – узлами. При этом внешняя нагрузка заменяется системой эквивалентных узловых сил. Такая дискретизация исходной конструкции и действующей нагрузки позволяет заменить ее расчет расчетом некоторой идеализированной системы с конечным числом степеней свободы.
Конечные элементы должны обладать постоянными жесткостными параметрами, а их напряженно-деформированное состояние должно с достаточной точностью описываться некоторыми аналитическими выраже-
112
ниями. Это важно для определения связи между узловыми усилиями и перемещениями.
Взависимости оттого, что принимается за неизвестные величины в узлах принято различать следующие разновидности метода конечных элементов. Если за основные неизвестные принять узловые усилия взаимодействия между элементами, то это соответствует методу конечных элементов в форме метода сил. Если в качестве основных неизвестных принять перемещения в узлах, то это соответствует методу конечных эле-
ментов в форме метода перемещений.
Внастоящее время метод конечных элементов является одним из наиболее распространенных численным методом, применяемым для расчета любых строительных конструкций и сооружений. Причем в расчетной практике преимущественно используется метод конечных элементов в форме метода перемещений.
12.1.2. Типы конечных элементов и их характеристики
По геометрической форме различают три типа простейших базовых конечных элемента, на которые могут разбиватьсяразличные конструкции:
одномерные;
двухмерные;
трехмерные.
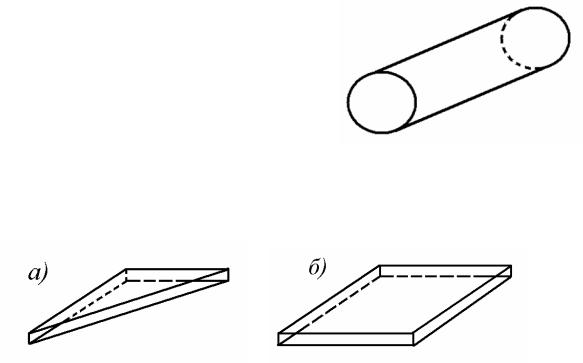
Одномерный конечный элемент
представляет собой призматический стержень (рис. 12.1).
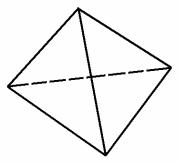
Двухмерный конечный элемент
может быть двух видов – треугольная пластина (рис. 12.2, а) и прямоугольная пластина (рис. 12.2, б).
Рис. 12.2
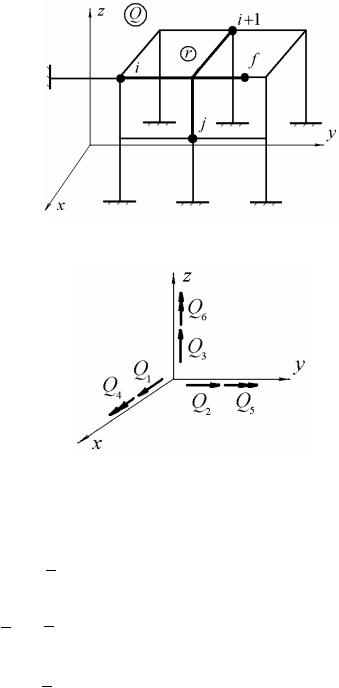
Трехмерный конечный элемент представляет собой тетраэдр
(рис. 12.3).
Наряду с перечисленными простейшими конечными элементами в качестве конечных элементов могут использоваться другие элементы бо-
113
лее сложной геометрической формы. Такими элементами могут быть любые геометрически неизменяемые части конструкции, для которых возможно получение зависимостей, описывающих их напряженнодеформированное состояние.
Конечные элементы характеризуются числом узлов и числом узловых реакций. Число узлов конечного элемента зависит от его формы и мерности. Например, число узлов у одномерного конечного элемента равняется двум, у двухмерного конечного элемента в виде треугольной пластины – трем, а виде четырехугольной пластины – четырем. Число узловых реакций у конечного элемента одного и того же типа может быть различным и
зависит от вида его напряженного состояния. Рассмотрим наиболее характерные случаи
напряженного состояния одномерного конечного элемента, которые могут встречаться при расчетах конструкций, и выясним, как, в зависимости от этого, может изменяться число узловых реакций.
Одномерный конечный элемент, работающий на растяжение-сжатие. Такой конечный элемент характеризуется двумя узловыми реакциями. В каждом
узле возникает одна реакция– продольная сила.
Одномерный конечный элемент, работающий на кручение. Такой конечный элемент также характеризуется двумя узловыми реакциями, но узловыми реакциями являются скручивающие моменты.
Одномерный конечный элемент, работающий на плоский изгиб в вертикальной плоскости или в горизонтальной плоскости. Число узловых реакций такого конечного элемента уже равно четырем. В каждом узле появляется по две реакции – поперечная сила и изгибающий момент.
Одномерный конечный элемент, работающий на растяжение-сжатие и на плоский изгиб в вертикальной плоскости или в горизонтальной плоскости. Такой конечный элемент характеризуется шестью узловыми реакциями. В каждом узле возникает по три реакции – одна продольная и поперечная силы и один изгибающий момент.
Одномерный конечный элемент, работающий на растяжение-сжатие, на кручение и изгиб в двух взаимно перпендикулярных плоскостях. Число узловых реакций у такого конечного элемента увеличивается до двенадцати. В каждом узле появляется по шесть реакций – одна продольная и две поперечных силы, один скручивающий и два изгибающих момента.
114
12.2.Расчет стержневых конструкций методом конечных элементов в форме метода перемещений
12.2.1. Постановка задачи
Рассмотрим произвольную пространственную стержневую конструкцию (рис. 12.4), для которой считаются известными все размеры геометрической схемы и поперечных сечений стержней. Геометрическая схема конструкции отнесена к декартовой координатной системе.
На заданную конструкцию действуют произвольная нагрузка, показанная на рис. 12.4 условным буквенным обозначением Q. Заданная конструкция считается линейно деформируемой системой. Разобьем конструкцию на конечные элементы, которые могут иметь произвольную геометрическую форму. Пусть число элементов равняется M и они соединены между собой в N узлах.
Считаем, что заданная произвольная нагрузка заменена эквивалентной узловой нагрузкой. Схема составляющих такой нагрузки в произвольном узле, в принятой координатной системе, показана на рис. 12.5.
Векторы с одинарной стрелкой соответствуют узловым силам, а векторы с двойной стрелкой – узло-
вым моментам. Тогда эквивалентная узловая нагрузка для конструкции в целом описывается следующим вектором нагрузки
|
Q |
|
|
1 |
|
|
|
|
Q Qj |
|
|
|
|
|
|
|
|
|
|
|
QN
115

Здесь
Qj1Qj2 Qj Qj3
Qj4Qj5Qj6
вектор нагрузки произвольного j-того узла (j=1,…, N).
Эквивалентная узловая нагрузка в общем случае определяется следующим образом. Для каждого конечного элемента из условия равенства возможных работ заданной нагрузки, действующей на элемент, и неизвестных узловых сил определяются эквивалентная узловая нагрузка для конечного элемента. Тогда эквивалентная узловая нагрузка для произвольного узла конструкции получается суммированием эквивалентных узловых нагрузок по всем элементам, сходящимся в этом узле.
12.2.2. Условия равновесия конструкции
Деформированное состояние конструкции в произвольном узле j в принятой координатной системе характеризуется тремя линейными перемещениями qj1, q12, qj3 и тремя угловыми перемещениями qj4, q15, qj6 (рис. 12.6) и, следовательно, описывается вектором следующего вида:
q j1q j2
q j3 q j q j4q j5q j6
Рис. 12.6
На рис. 12.6 векторы с одинарной стрелкой соответствуют линейным перемещениям, а векторы с двойной стрелкой – угловым перемещениям узлов. Тогда деформированное состояние конструкции в целом будет опи-
сываться вектором перемещений
116
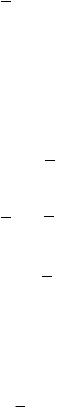
q1 |
|
|
|
|
|
|
|
|
|
|
|
q q j |
|
(12.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
qN |
|
||
Согласно принятой схеме деформированного состояния конструкции ее напряженное состояние в произвольном узле j будет характеризоваться тремя силовыми реакциями Rj1, R12, Rj3 и тремя моментными реакциями Rj4, R15, Rj6 и описывается вектором
Rj1Rj2 Rj Rj3
Rj4Rj5Rj6
а напряженное состояние конструкции в целом описывается вектором
внутренних узловых усилий
|
R |
|
|
|
1 |
|
|
|
|
|
|
R |
Rj |
|
(12.2) |
|
|
|
|
|
|
|
|
R |
|
|
|
|
N |
|
|
Вектор узловых перемещений (12.1) и вектор внутренних узловых усилий (12.2) характеризуют напряженно-деформированное состояние конструкции. При использовании метода перемещений они связаны между
собой следующей линейной зависимостью |
|
R k q |
(12.3) |
где k – матрица жесткости конструкции.
Матрица жесткости конструкции имеет блочную структуру
|
|
k11 |
k |
|
|
|
||
|
|
kN1 |
|
|
|
k1N |
|
|
|
|
|
(12.4) |
|
|
|
|
kNN |
|
||
117
Каждый блок матрицы жесткости конструкции представляет собой подматрицу единичных реакций, возникающих в произвольном узле, и, в общем случае, имеет размеры 6х6
k j1f 1 |
k j1f 6 |
k jf |
|
|
k j6f 6 |
k j6f 1 |
j, f 1,..., N
Поскольку в качестве неизвестных величин для рассматриваемой разновидности метода конечных элементов принимаются узловые перемещения, то основными уравнениями будут условия равновесия узловых точек. Условия равновесия отдельных узлов конструкции описываются соотношениями
Rj Qj 0 |
j 1,..., N , |
а условия равновесия для конструкции в целом имеют вид
R Q 0 .
Тогда с учетом зависимости (13.13) условия равновесия конструкции примут вид
k q Q 0 . |
(12.5) |
12.2.3. Матрица жесткости конструкции
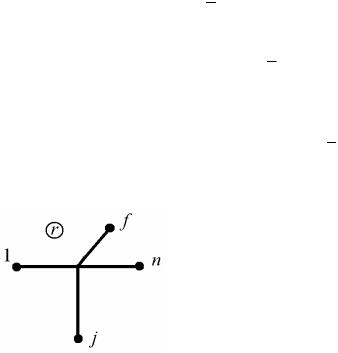
Деформированное состояние отдельного конечного элемента номера r (рис. 12.7) в произвольном узле j характеризуется собственными линей-
|
ными перемещениями |
qr |
,qr |
,qr |
и угловыми пе- |
|||||
|
|
|
|
|
|
j1 |
|
j2 |
j3 |
|
|
ремещениями |
qr |
|
,qr |
,qr |
|
и, |
следовательно, опи- |
||
|
|
|
j4 |
j5 |
j6 |
|
|
|
||
Рис. 12.7 |
сывается вектором |
|
|
|
|
|
|
|||
|
|
qr |
|
|
|
|
|
|
|
|
|
|
|
j1 |
|
|
|
|
|
|
|
|
|
qr |
|
|
|
|
|
|
|
|
|
|
|
j2 |
|
|
|
|
|
|
|
|
|
qr |
|
|
|
|
|
|
|
|
|
qr |
j3 |
|
|
|
|
|
|
|
|
|
j |
qr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
j4 |
|
|
|
|
|
|
|
|
|
qrj5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qr |
|
|
|
|
|
|
|
|
|
|
|
j6 |
|
|
|
|
|
|
|
118

Тогда деформированное состояние в целом отдельного конечного элемента, имеющего n узлов, будет описываться вектором перемещений
|
|
qr |
||
|
|
|
1 |
|
|
|
|
|
|
q |
r |
|
r |
|
|
q j |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
qr |
||
|
|
|
n |
|
В соответствии с принятой схемой деформирования отдельного конечного элемента его напряженное состояние в произвольном узле j харак-
теризуется тремя силовыми реакциями Rrj1, Rrj2, Rrj3 и тремя моментными реакциями Rrj4, Rrj5, Rrj6 и описывается вектором
|
|
Rr |
|
|
|
j1 |
|
|
Rr |
|
|
|
|
j2 |
|
|
Rr |
|
|
Rr |
j3 |
|
|
j |
Rr |
|
|
|
|||
|
|
j4 |
|
|
Rrj5 |
|
|
|
|
|
|
|
Rr |
|
|
|
|
j6 |
|
а напряженное состояние в целом отдельного конечного элемента, будет описываться следующим вектором внутренних узловых усилий
|
|
Rr |
||
|
|
|
1 |
|
|
|
|
|
|
R |
r |
|
r |
|
|
Rj |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Rr |
||
|
|
|
n |
|
Вектор узловых перемещений и вектор внутренних узловых усилий отдельного конечного элемента, как и для конструкции в целом, связаны между линейной зависимостью
Rr k r qr |
(12.6) |
где k r – матрица жесткости отдельного конечного элемента. Эта мат-
рица устанавливает связь между перемещениями узлов системы и реакциями в связях, соответствующих принятым степеням свободы.
119

Матрица жесткости отдельного конечного элемента также имеет блочную структуру
|
|
k11 |
r |
|
r |
k r |
|
|
k1n |
||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
kn1 |
|
r |
|
|
|
|
knn |
||
Каждый блок матрицы жесткости отдельного конечного элемента тоже представляет собой подматрицу единичных реакций, возникающих в произвольном узле конечного элемента, и, в общем случае, имеет размеры 6х6
krj1f 1k jf r
krj6f 1
krj1f 6 |
|
|
|
|
|
|
j, f 1,...,n |
|
|||
|
r |
|
|
|
|
|
|
k j6f 6 |
|
|
|
Определение элементов матрицы жесткости k r в общем случае основывается на использовании принципа возможных перемещений деформируемой системы или на использовании теоремы Клапейрона. В случае одномерных конечных элементов для определения элементов подматриц можно использовать готовые единичные эпюры внутренних усилий, полученные для отдельных прямолинейных стержней в методе перемещений.
Установим связь величин, характеризующих напряженнодеформированное состояние конструкции в целом и образующих ее отдельных конечных элементов. Вектор внутренних узловых усилий в произвольном узле j зависит от узловых перемещений конструкции и согласно принципу суперпозиции описывается соотношением
Rj Rjf . f
В свою очередь доля этого вектора, связанная с перемещением произвольного узла конструкции f, будет складываться из векторов внутренних узловых усилий тех конечных элементов, которые примыкают к узлам конструкции j и f
Rjf |
Rrjf . |
(12.7) |
|
r j, f |
|
Входящие в (12.7) доли векторов внутренних узловых усилий конструкции Rjf и отдельных конечных элементов Rrjf , описываются линейными соотношениями
Rjf k jf q f |
(12.8) |
120
