
Турищев Л.С. (сост.) Строительная механика. Часть 2. Статически неопределимые системы. ПГУ, 2009
.pdf
матрица влияния изгибающих моментов заданной статически неопределимой системы. В случае действия сочетания k нагрузок изгибающие моменты определяются по формуле
M LM G |
(8.46) |
При одной схеме нагружения матричные формулы для определения двух других внутренних усилий имеют вид:
– для поперечных сил
Q LQG
где LQ L0QP L0q X – матрица влияния поперечных сил заданной системы;
– для продольных сил
N LNG
где LN L0NP L0n X – матрица влияния продольных сил заданной системы.
В случае действия сочетания k нагрузок поперечные и продольные силы определяются, соответственно, по формулам
|
Q LQG |
и |
N LNG . |
Кинематическая поверка правильности нахождения внутренних усилий с учетом только изгибных деформаций заключается в проверке соблюдения условия
L0m BM M 0.
В случае, если учитываются и продольных деформаций, это условие приобретает вид
L0m BM M L0n Bn N 0.
8.5. Определение перемещений в плоских статически неопределимых стержневых конструкциях
8.5.1. Особенности определения перемещений от нагрузки
Так как вывод формулы Максвелла – Мора
i mEIiM ds nEAi N ds k qGAiQds |
|||
k l |
z |
k l |
k l |
не зависит от статических свойств стержневой конструкции, то она справедлива и для определения перемещений в статически неопределимых стержневых конструкциях при действии на них произвольной нагрузки.
51

При этом следует учитывать, что для определения каждого перемещения в статически неопределимой системе потребуется определять в ней внутренние усилия дважды – при рассмотрении действительного состояния и вспомогательного единичного состояния.
Однако, при определении перемещений в статически неопределимой стержневой конструкции вспомогательное единичное состояние, связанное с определяемым перемещением, можно образовывать в любой статически определимой системе, полученной из заданной системы. Обоснованием этому служит то обстоятельство, что любая такая статически определимая система может рассматриваться как основная система метода сил. Поэтому определение перемещения в заданной статически неопределимой системе может быть заменено определением перемещения в эквивалентной ей статически определимой основной системе.
Таким образом, формула Максвелла – Мора при определении перемещений в статически неопределимых стержневых конструкциях в общем случае имеет вид
i |
m0M |
ds |
n0N |
ds k |
q0Q |
|
|
EIi |
EAi |
GAi |
ds |
(8.47) |
|||
k l |
z |
k l |
|
k l |
|
|
|
где mi0, ni0, qi0 – внутренние усилия вспомогательного единичного состояния, найденные в любой статически определимой системе, полученной из заданной системы.
8.5.2. Определение перемещений от температуры и осадки опор
Так как при действии температуры и осадки опор на статически неопределимые стержневые конструкции в них возникают внутренние усилия, то они оказывают влияние на перемещения таких конструкций. Поэтому ранее полученные рабочие формулы для определения перемещений в статически определимых стержневых конструкциях от температуры
it0 |
ni0 tо mi0 t ds |
(8.48) |
|
|
k |
l |
|
и осадки опор |
|
|
|
|
i0 |
rji0cj |
(8.49) |
|
|
j |
|
не справедливы для статически неопределимых систем.
52

При получении рабочих формул для определения перемещений в плоских статически неопределимых стержневых конструкциях от температуры и осадки опор используем эквивалентность основной системы метода сил заданной системе. Внешними воздействиями для основной системы являются основные неизвестные метода сил, играющие роль внешней нагрузки, и температура и осадки опор.
С учетом этого согласно принципу суперпозиции можно записать искомое перемещение в виде
|
i |
0 |
0 |
0 |
(8.50) |
|
iX |
it |
is |
|
где iX0 – доля искомого перемещения, связанная с влиянием основных неизвестных; it0 , is0 – доли искомого перемещения, порождаемые непо-
средственно температурой или осадкой опор.
Тогда, подставляя в (8.50) (8.47) и (8.48), получим рабочую формулу для определения перемещений в плоских статически неопределимых стержневых конструкциях от температуры
i mEIi0M ds nEAi0N ds k qGAi0Qds ni0 tо mi0 t ds . |
||||
k l |
z |
k l |
k l |
k l |
Подставляя в (8.50) (8.47) и (8.49), получим рабочую формулу для определения перемещений в плоских статически неопределимых стержневых конструкциях от осадки опор
i mEIi0M ds nEAi0N ds k qGAi0Qds rji0cj . |
||||
k l |
z |
k l |
k l |
j |
8.5. Резюме
В основе расчета стержневых конструкций методом сил лежит переход от заданной статически неопределимой системы к расчету основной системы. Основной системой метода сил может быть любая эквивалентная статически определимая система, полученная из заданной путем удаления ее лишних связей. Эквивалентность двух систем должна состоять в одинаковости внутренних усилий – статическая эквивалентность, и одинаковости перемещений – кинематическая эквивалентность.
Канонические уравнения метода сил представляют собой систему неоднородных линейных алгебраических уравнений относительно основ-
53
ных неизвестных. Основные неизвестные метода сил являются реакциями удалённых лишних связей.
Для определения внутренних усилий в заданной системе согласно принципу суперпозиции складываются внутренние усилия, полученные в основной системе от основных неизвестных, заданной нагрузки, температуры и осадки опор.
Для проверки правильности хода вычислений внутренних усилий и полученных их значений выполняется ряд промежуточных и окончательных поверок.
Использование свойств симметрии заданной системы при образовании основной системы позволяет разделить основные неизвестные на симметричные и антисимметричные величины, которые находятся независимо друг от друга.
Для применения аппарата матричной алгебры к расчету заданной системы методом сил необходимо осуществить дискретизацию расчетной схемы стержневой конструкции и действующей на нее нагрузки.
8.6. Материалы для самоконтроля
Проверьте, как Вы усвоили следующие понятия, определения, алгоритмы и формулы:
–заданная система;
–основная система;
–канонические уравнения;
–формулы для вычисления коэффициентов канонических уравнений;
–формулы для вычисления свободных членов канонических урав-
нений;
–единичные состояния основной системы;
–состояния основнойсистемы при приложении внешних воздействий;
–методы решения канонических уравнений;
–формулы для определения окончательных внутренних усилий;
–проверки метода сил;
–упрощения метода сил;
–идеальная основная система;
–рациональная основная система;
–симметричная основная система;
–группировка основных неизвестных;
54
–вектор основных неизвестных;
–матрица основных неизвестных;
–матрица податливости основной системы;
–формула для вектора основных неизвестных;
–формулы для векторов окончательных внутренних усилий;
–особенности использования формулы Максвелла–Мора для статически неопределимых стержневых конструкций;
–формулы для определения перемещений от температуры и осадки опор для статически неопределимых стержневых конструкций.
Проверьте, как Вы умеете при расчете статически неопределимых стержневых систем методом сил:
–образовывать основную систему;
–составлять систему канонических уравнений;
–образовывать единичные состояния и строить эпюры m, q, n;
–образовывать грузовое состояние и строить эпюры M, Q, N;
–находить коэффициенты и свободные члены канонических урав-
нений.
Проверьте, можете ли Вы вывести:
–канонические уравнения и формулы для расчёта n-раз статически неопределимой стержневой системы методом сил на действие нагрузки, температуры и осадки опор;
–формулы для осуществления промежуточных и окончательных проверок метода сил;
–матричные формулы для определения векторов внутренних усилий для n-раз статически неопределимой стержневой системы при действии нагрузки;
–формулы для определения перемещений в статически неопределимых стержневых конструкциях от действия температуры и осадки опор.
55
М-9. РАСЧЕТ ДВУХШАРНИРНОЙ АРКИ
9.0. Введение в модуль
Основной целью модуля является получение формул для определения внутренних усилий в двухшарнирной арке от неподвижной нагрузки.
Структура изучаемого модуля включает следующие учебные элементы:
1.Применение метода сил для расчета двухшарнирной арки.
2.Определение внутренних усилий в двухшарнирной арке от неподвижной нагрузки.
3.Поверки правильности расчета двухшарнирной арки.
При изучении учебных элементов рекомендуется использование сле-
дующей литературы: [3, c. 293 – 308]; [4, c. 366 – 370].
9.1. Применение метода сил для расчета двухшарнирной арки
9.1.1. Постановка задачи
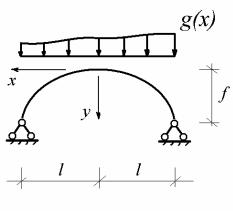
Будем рассматривать двухшарнирную арку с опорами в одном уровне и имеющую некоторое симметричное очертание согласно заданному закону
y f ( x ) (рис. 9.1).
Степень полной статической неопределимости заданной двухшарнирной арки равняется
Л 1
Поперечное сечение арки имеет переменные размеры по длине ее оси. Изменения геометрических характеристик поперечного сечения (площадь, момент
инерции) вдоль оси арки описываются некоторыми заданными функциями
A A s ; |
Iz Iz s |
56
Геометрические характеристики в замковом сечении имеют, соответственно, значения A0, I0 .
На арку действует произвольная неподвижная вертикальная нагрузка, показанная на рис.8.1 условно как распределенная нагрузка с переменной интенсивностью. Ставится задача для заданной системы определить опорные реакции и внутренние усилия M, Q, N, возникающие в произвольном сечении арки. Заданная система считается линейно деформируемой.
Двухшарнирные арки симметричного очертания с опорами в одном уровне имеют широкое распространение в строительной практике, а действующие на них реальные неподвижные нагрузки, как правило, являются вертикальными.
9.1.2. Основная система и каноническое уравнение
Для образования основной системы метода сил необходимо в заданной системе удалить одну лишнюю связь и получить статически определимую систему. Возможны два варианта получения статически определимой системы – балочный и арочный.
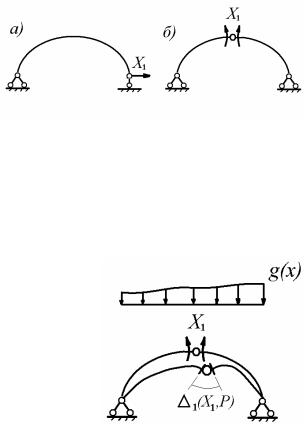
Первый вариант связан с удалением горизонтального опорного стержня на одной из опор двухшарнирной арки. Полученная статически определимая система
представляет собой кривой брус, опертый по балочной схеме (рис. 9.2, а) Второй вариант связан с введением шарнира в замковое сечение двух-
шарнирной арки. В этом случае статически определимой системой является трехшарнирная арка (рис. 9.2, б). Исходя из близости восприятия нагрузок трехшарнирной и двухшарнирной арками для образования основной системы, выберем второй вариант статически определимой системы.
Статическая эквивалентность трех-
шарнирной арки заданной системе достигается приложением к ней в качестве дополнительного внешнего воздействия реакции удаленной лишней связи X1 , изгибающего момента в замковом сечении двухшарнирной арки (рис. 9.3).
Эта реакция X1 является основным неизвестным метода сил при расчете двухшарнирной арки.
57

Кинематическая эквивалентность двух систем достигается введе-
нием требования обращения в нуль взаимного угла поворота торцов в замковом шарнире
1 X1, P 0. |
(9.1) |
Данное перемещение вызвано основным неизвестным и заданной внешней нагрузкой.
Трехшарнирная арка, для которой соблюдаются требования ее статической и кинематической эквивалентностей с заданной системой, и является основной системой метода сил для двухшарнирной арки.
Основная система, как и заданная, считается линейно-дефор- мируемой системой. Поэтому, согласно принципу суперпозиции, взаимный угол поворота торцов в замковом шарнире будет складываться из частичного перемещения 1X1 , вызванного действием основного неизвестно-
го, и частичного перемещения 1P , вызванного действием нагрузки. Сле-
довательно, условие (9.1) примет вид |
|
1X1 1P 0 . |
(9.2) |
Так как изменения частичного перемещения 1X1 и основного неиз-
вестного X1 связаны прямой пропорциональной зависимостью, то |
|
1X1 11X1 , |
(9.3) |
где 11 – единичный взаимный угол поворота торцов в замковом шарнире
основной системы от действия безразмерного момента X1 |
1. |
С учетом (9.3) условие (9.2) примет вид уравнения |
|
11X1 1P 0. |
(9.4) |
Полученное уравнение (9.4) и является каноническим уравнением метода сил для двухшарнирной арки. Для его решения и нахождения основного неизвестного X1 необходимо определить коэффициент при основном не-
известном 11 и свободный член канонического уравнения 1P .
9.1.3. Особенности определения коэффициента исвободного члена
Поскольку коэффициент при основном неизвестном и свободный член канонического уравнения являются перемещениями, возникающими в трехшарнирной арке от нагрузки (соответственно, единичной или заданной), то для их определения используется формула Максвелла – Мора. Эта формула для определения единичного перемещения 11 имеет вид
11 |
m2 |
ds |
n2 |
|
|
|
1 |
1 |
ds |
(9.5) |
|||
s |
EI |
z |
s |
EA |
|
|
|
|
|
|
|||
58
а при определении перемещения от действия нагрузки 1P принимает вид
1P m1M P ds n1NP ds |
(9.6) |
||||
s |
EI |
z |
s |
EA |
|
|
|
|
|||
Из формул (9.5), (9.6) следует, что при определении коэффициента и свободного члена необходимо учитывать влияние, как изгибающих моментов, так и продольных сил. Интегрирование в этих формулах ведется по длине оси арки.
Для нахождения коэффициента при основном неизвестном по формуле (9.5) нужно определить единичные внутренние усилия m1, n1. Для
нахождения свободного члена канонического уравнения по формуле (9.6), кроме того, нужно определить внутренние усилия от заданной нагрузки
MP , NP .
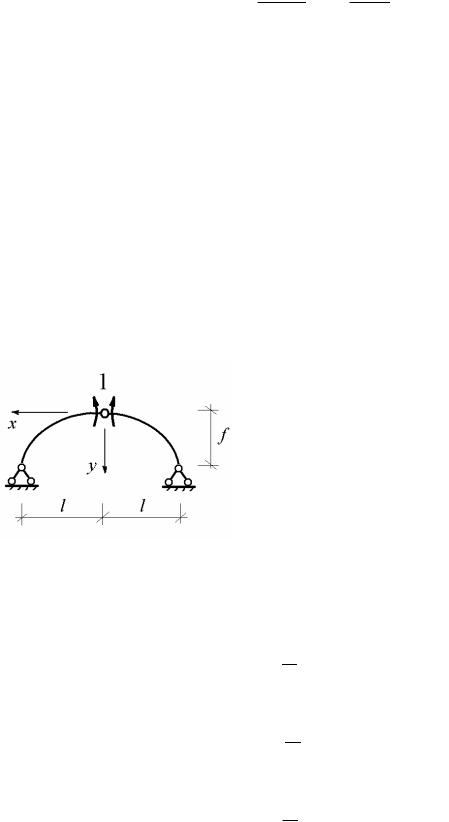
С целью определения единичных внутренних усилий m1, n1 образуем единичное состояние, загружая основную систему безразмерным моментом X1 1 (рис. 9.4).
В опорных закреплениях единичного состояния вертикальные составляющие опорных реакций не возникают, а единичный распор равен
h |
1 . |
(9.7) |
|
f |
|
Знак минус говорит о том, что единичный распор направлен наружу от контура арки.
С учетом полученных величин опорных реакций единичные внутренние усилия в произвольном сечении описываются следующими формулами:
единичный изгибающий момент
m |
1 f y |
(9.8) |
1 |
f |
|
|
|
единичная поперечная сила
q |
1 sin |
(9.9) |
1 |
f |
|
|
|
единичная продольная сила
n |
1 cos |
(9.10) |
1 |
f |
|
|
|
59
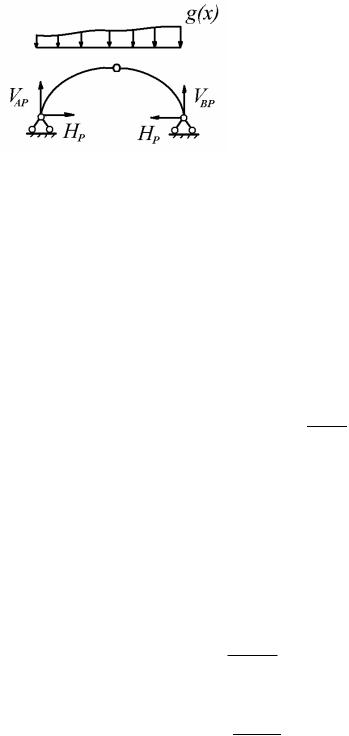
С |
целью определения |
внутренних усилий от заданной нагрузки |
MP , NP |
образуем грузовое состояние, нагружая основную систему задан- |
|
ной нагрузкой (рис. 9.5). |
|
|
Опорные реакции VAP , |
VBP , HP и внутренние усилия MP , QP , NP в |
|
грузовом состоянии определяются по формулам, полученным для расчета трехшарнирной арки при действии неподвижной вертикальной нагрузки в модуле М-5 первой части курса.
Так как единичные внутренние усилия m1 , n1 и грузовые внутренние усилия MP , NP всегда описываются нелинейными функциями, а их эпюры имеют криволиней-
Рис. 9.5 ное очертание, то при вычислении интегралов, входящих в формулу Максвелла – Мора нельзя пользоваться правилом Верещагина. В этом случае для их вычисле-
ния необходимо применять численные методы. Такие методы основаны на приближенном вычислении площади графика подынтегральной функции. Применим для вычисления определенных интегралов, входящих в формулы (9.5), (9.6), метод трапеций.
С этой целью осуществим следующие преобразования в формулах (9.5), (9.6). Так как единичные и грузовые внутренние усилия зависят от абсциссы сечения x, то с помощью подстановки
ds dx cos
прежде всего, поменяем переменную интегрирования. Кроме того, подставим в них единичные внутренние усилия (9.8) и (9.10). И, наконец, умножим и поделим первые интегралы этих формул на изгибную жесткость замкового сечения EI0 , а вторые интегралы - на продольную жесткость
замкового сечения EA0 .
С учетом проделанных преобразований формулы (9.5) и (9.6) примут вид
11 |
|
|
1 |
2 |
( 3dx r02 |
4dx) |
(9.11) |
|
|
EI0 f |
|
2l |
2l |
|
|
и |
|
|
|
|
|
|
|
1P |
f |
1 |
|
( 1dx r02 |
2dx) |
(9.12) |
|
|
|
EI |
2l |
2l |
|
||
|
|
|
|
0 |
|
||
60
