
Турищев Л.С. (сост.) Строительная механика. Часть 2. Статически неопределимые системы. ПГУ, 2009
.pdf
и
Rrjf k jf r qrf |
(12.9) |
Подставляя (12.8), (12.9) в (12.7) и учитывая совместность узловых перемещений конструкции и отдельных конечных элементов, получим соотношение, связывающее подматрицы единичных реакций узлов конструкции с подматрицами единичных узловых реакций отдельных конечных элементов
k jf k jf r r jf
С учетом полученного соотношения матрица жесткости конструкции (12.4) принимает вид
|
k11 |
r |
|
k1N |
r |
|
|
|
|
|
|
|
|||
|
r 1,1 |
|
|
|
r 1,N |
|
|
|
|
|
|
|
|
||
k |
|
|
|
(12.10) |
|||
|
kN1 |
r |
|
|
r |
|
|
|
|
kNN |
|
||||
r N ,1 |
|
|
|
r N ,N |
|
|
|
Полученную матрицу жесткости необходимо подчинить условиям опирания конструкции. Для этого из нее необходимо исключить строки и столбцы, соответствующие узловым перемещениям, по направлению которых наложены кинематические связи.
12.2.3. Матрицы жесткости одномерного конечного элемента
Деформированное состояние одномерного конечного элемента, имеющего два узла (рис. 12.1), в общем случае описывается вектором
|
q r |
|
(12.11) |
qr |
i |
|
|
qr |
|
|
|
|
i 1 |
|
|
|
|
Элементами вектора (12.11) являются векторы узловых перемещений |
||||||||
q r |
и |
q r |
. Тогда соответствующая (12.11) матрица жесткости конечного |
|||||||
i |
|
i 1 |
|
|
|
|
|
|
|
|
элемента будет иметь следующую структуру |
|
|
|
|||||||
|
|
|
|
kii |
r |
|
kii 1 |
r |
|
|
|
|
|
k r |
|
|
|
|
(12.12) |
||
|
|
|
|
ki 1i |
|
r |
ki 1i 1 |
|
r |
|
|
|
|
|
|
|
|
||||
Элементами матрицы (12.12) являются подматрицы единичных узловых реакций. Размеры элементов (12.11) и (12.12) могут быть различными в зависимости от вида напряженного состояния одномерного конечного элемента.
121
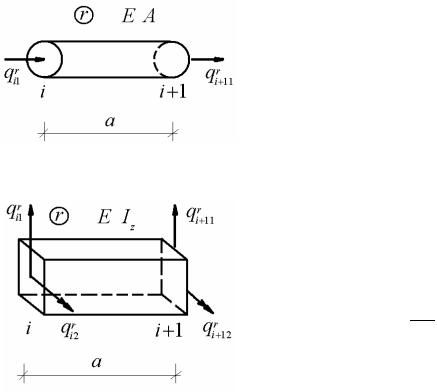
Для одномерного конечного элемента, работающего на растяжениесжатие, деформированное состояние в каждом узле характеризуется одним перемещением (рис. 12.8). Тогда вектор (12.11) принимает вид
|
qr |
|
q r |
i1 |
, |
qr |
|
|
|
i 11 |
|
а матрица (12.12) принимает вид
k r |
|
kr |
kr |
|
(12.13) |
|
i1i1 |
i1i 11 |
. |
||
|
kr |
kr |
|
|
|
|
|
i 11i1 |
i 11i 11 |
|
|
Элементы матрицы (12.13) являются единичными узловыми реакциями. Так, например, kir1i1 – это реакция в i –том узле конечного элемента,
|
вызванная перемещением на единицу это- |
|||||||||||
|
го же узла в продольном направлении, а |
|||||||||||
|
kr |
|
– это реакция в i-том узле конечного |
|||||||||
|
i1i 11 |
|
|
|
|
|
|
|
|
|
||
|
элемента, вызванная перемещением на |
|||||||||||
|
единицу узла i+1 в продольном направле- |
|||||||||||
|
нии. |
|
Точно также два |
других элемента |
||||||||
|
kr |
|
и kr |
|
|
характеризуют реакции в |
||||||
Рис. 12.8 |
i 1i1 |
|
i 11i 11 |
|
|
|
|
|
|
|||
i+1-ом узле, обусловленные соответствую- |
||||||||||||
|
||||||||||||
|
щими единичными перемещениями. С уче- |
|||||||||||
|
том |
значений |
|
перечисленных |
единичных |
|||||||
|
реакций, полученных с помощью единич- |
|||||||||||
|
ных эпюр, матрица (12.13) имеет вид |
|||||||||||
|
|
|
k |
r |
|
|
EA |
|
1 |
-1 |
(12.14) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a |
|
-1 |
1 |
|
|
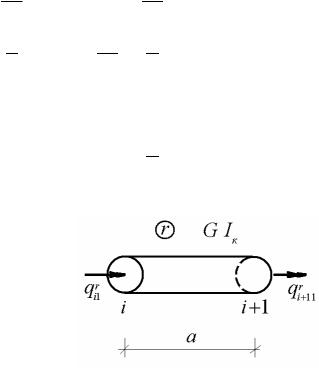
Для одномерного конечного элемента, работающего на плоский изгиб в Рис. 12.9 вертикальной плоскости, деформирован-
ное состояние в каждом узле характеризуется двумя перемещениями
(рис. 12.9).
Тогда вектор (12.11) принимает вид
qir1 qr qir2qir 11
qir 12
122
а матрица (12.12) принимает вид
|
|
kr |
kr |
kr |
kr |
|
|
|
|
i1i1 |
i1i2 |
i1i 11 |
i1i 12 |
|
|
k r |
|
kr |
kr |
kr |
kr |
|
(12.15) |
|
i2i1 |
i2i2 |
i2i 11 |
i2i 12 |
|
||
|
kir 111i1 |
kir 11i2 |
kir 11i 11 |
kir 11i 12 |
|
|
|
|
|
r |
r |
r |
r |
|
|
|
ki 12i1 |
ki 12i2 |
ki 12i 11 |
ki 12i 12 |
|
|
|
С учетом значений единичных реакций, полученных с помощью единичных эпюр, матрица (12.15) имеет вид
|
|
|
12 |
|
6 |
|
|
12 |
6 |
|
|
||||
|
|
|
|
3 |
|
|
2 |
|
|
3 |
|
2 |
|
|
|
|
|
a |
|
a |
|
|
|
a |
|
a |
|
|
|
||
|
|
|
|
|
|
4 |
|
|
6 |
2 |
|
|
|||
k |
r |
|
|
|
|
a |
|
a2 |
a |
|
(12.16) |
||||
|
EIz |
|
|
|
|
|
|
12 |
|
6 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
a3 |
a2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
симметрично |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
a |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При плоском изгибе одномерного конечного элемента в горизон- |
|||||||||||||||
тальной плоскости в (12.16) изгибная же- |
|
|
|
|
|
|
|
||||||||
сткость EIz заменится на EIy . |
|
|
|
|
|
|
|
|
|
|
|
||||
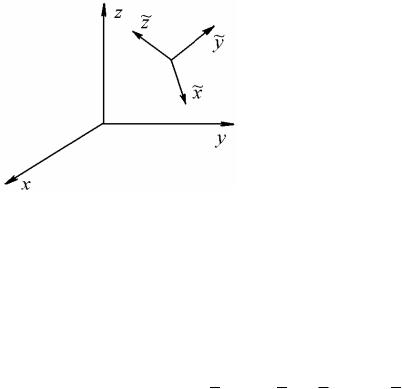
Для одномерного конечного элемен- |
|
|
|
|
|
|
|
||||||||
та, работающего на кручение, деформиро- |
|
|
|
|
|
|
|
||||||||
ванное состояние в каждом узле характери- |
|
|
|
|
|
|
|
||||||||
зуется одним перемещением (рис.12.10). |
|
|
|
|
|
|
|
|
|||||||
Тогда вектор (12.11) принимает вид |
|
|
|
|
|
Рис. 12.10 |
|
||||||||
|
|
|
|
|
|
|
qr |
|
|
|
|
|
|
|
|
|
|
|
|
q r |
|
i1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qr |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
i 11 |
|
|
|
|
|
|
|
|
а матрица (12.12) принимает вид |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
kr |
|
|
kr |
|
|
|
|
|
|
(12.17) |
|
|
k r |
i1i1 |
|
i1i |
11 |
|
|
|
|
|
||||
|
|
|
|
kr |
|
|
kr |
|
|
|
|
|
|
|
|
|
|
|
|
|
i 11i1 |
i 11i 11 |
|
|
|
|
|
|
|||
С учетом значений единичных реакций, полученных с помощью единичных эпюр, матрица (12.17) имеет вид
k |
r |
|
GI |
|
1 |
-1 |
|
(12.18) |
|
a |
к |
-1 |
1 |
|
|||
|
|
|
|
|
|
123
Для различных случаев сложного напряженного состояния, получаемого вследствие совместного учета растяжения-сжатия, плоского изгиба и кручения, матрицы жесткости получаются объединением соответствую-
щих элементов матриц (12.14), (12.16), (12.18).
12.2.4. Матрица преобразования координат
При выводе формулы (12.10), позволяющей формировать матрицу жесткости конструкции из матриц жесткости конечных элементов, неявно предполагается, что конструкция и ее конечные элементы относятся к общей системе координат. В случае несовпадения систем координат необходимо осуществлять преобразование матриц жесткости конечных элементов.
Рассмотрим две координатные системы – общую x, y, z и местную x, y, z (рис. 12.11).
Общая координатная система ис-
пользуется для получения матрицы жесткости конструкции в целом, а местная координатная система – для получения матриц жесткости отдельных конечных элементов.
Известно, что переход от одной ко-
Рис. 12.11
ординатной системы к другой можно осуществлять с помощью некоторой мат-
рицы преобразования координат T . Для конечных элементов такая
матрица является ортогональной, и она позволяет связывать векторы узловых перемещений
q r T q r , |
q r T qr |
(12.19) |
и векторы узловых реакций
Rr T Rr , |
Rr T Rr |
(12.20) |
в общей и местной координатной системах.
Тогда из (12.20) с учетом зависимостей (12.6), (12.19) можно получить следующую формулу для определения матрицы жесткости конечного элемента при переходе от местной координатной системы к общей системе
k r T k r T |
(12.21) |
124
В общем случае напряженно-деформированного состояния, характеризуемого 12 узловыми перемещениями, структура матрицы преобразования координат T определяется из зависимости (12.19) и имеет вид
l
T l l
Здесь
lx |
mx |
|
my |
l ly |
|
|
mz |
lz |
l
nx ny nz
матрица ориентации местной системы координат относительно общей. Ее элементами являются значения направляющих косинусов. При уменьшении числа узловых перемещений одномерного конечного элемента соответствующим образом может изменяться структура матрицы T , а часть элементов матрицы ориентации принимать нулевые значения.
12.2.5. Общая схема использования метода конечных элементов
Метод конечных элементов в форме метода перемещений включает следующие основные этапы:
1.Разбиение конструкции на конечные элементы, задание геометрических и жесткостных параметров каждого элемента, определение положения узловых точек в общей системе координат.
2.Формирование вектора эквивалентной узловой нагрузки.
3.Нахождение матриц жесткости конечных элементов в местной системе координат.
4.Формирование матрицы преобразования координат.
5.Определение матриц жесткости конечных элементов в общей системе координат.
6.Получение матрицы жесткости для всей конструкции и подчинение ее условиям опирания конструкции.
7.Нахождение узловых перемещений конструкции.
8.Определение параметров напряженного состояния элементов конструкции.
125
12.5. Резюме
Основная идея метода конечных элементов состоит в том, что рассчитываемая строительная конструкция заменяется совокупностью некоторых элементов, соединенных между собой и с основанием в конечном числе точек. При этом внешняя нагрузка заменяется системой эквивалентных узловых сил.
Базовыми конечными элементами, на которые могут разбиваться различные конструкции, являются одномерные, двухмерные и трехмерные элементы.
Конечные элементы характеризуются числом узлов и числом узловых реакций. Число узлов конечного элемента зависит от его формы и мерности. Число узловых реакций у конечного элемента одного и того же типа может быть различным и зависит от вида его напряженного состояния.
Метод конечных элементов является одним из наиболее распространенных численных методов, применяемых для расчета строительных конструкций, и он имеет две разновидности – в форме метода сил и в форме метода перемещений. В расчетной практике преимущественно используется метод конечных элементов в форме метода перемещений.
Расчет методом конечных элементов в форме метода перемещений основан на использовании матрицы жесткости конструкции. Такая матрица формируется на основе матриц жесткости конечных элементов, на которые разбита конструкция.
Элементами матриц жесткости конечных элементов являются единичные узловые реакции. Их число может быть различным в зависимости от вида напряженного состояния одномерного конечного элемента.
12.6. Материалы для самоконтроля
Проверьте, как Вы усвоили следующие понятия, определения, алгоритмы и формулы:
–суть метода;
–конечный элемент;
–узел;
–типы конечных элементов;
126
–вектор перемещений конструкций;
–вектор нагрузки конструкций;
–матрица жёсткости конструкций;
–вектор перемещений конечного элемента;
–матрица жёсткости конечного элемента. Проверьте, как Вы умеете:
–разбивать конструкцию на конечные элементы;
–нумеровать конечные элементы, узлы и узловые перемещения в общей системе координат;
–составлять вектор перемещений для конструкции;
–составлять вектор перемещений для узла;
–составлять матрицу жёсткости для конструкции;
–составлять блоки матрицы жёсткости для конструкции;
–нумеровать узлы и узловые перемещения для конечного элемента
–в местной системе координат;
–составлять вектор перемещений для конечного элемента;
–находить элементы матриц жёсткости.
127
М-13. ОСНОВЫ РАСЧЕТА СТЕРЖНЕВЫХ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ
13.0. Введение в модуль
Основными целями модуля являются:
рассмотрение понятия несущей способности конструкции и методов ее определения;
анализ причин достижения стержневыми конструкциями предельного состояния равновесия;
получение условия выключения из работы сжато-растянутого стержня;
получение условия выключения из работы изогнутого стержня;
определение несущей способности для частных случаев стержневых конструкций.
Структураизучаемогомодуля включаетследующие учебныеэлементы: 1. Существующие подходы к определению несущей способности
стержневых конструкций 2. Условия выключенияизработынаиболееслабых местконструкции.
3. Определение несущей способности ферм.
4. Определение несущей способности стержневых конструкций, работающих на изгиб.
При изучении учебных элементов рекомендуется использование сле-
дующей литературы: [4, c. 416 – 428]; [5, c. 420 – 444].
13.1.Существующие подходы к определению несущей способности стержневых конструкций
Под несущей способностью понимается величина предельной нагрузки, которую конструкция может выдержать, удовлетворяя требованиям прочности и устойчивости. По мере развития строительной механики подходы к определению несущей способности конструкций менялись.
128

Первый подход определения несущей способности основан на использовании принципа расчета конструкций по рабочему состоянию. Согласно этому принципу величины, характеризующие напряженно-дефор- мированного состояния конструкции (внутренние усилия, напряжения, перемещения), определяются при действующей рабочей нагрузке и соответствуют упругой стадии работы конструкции. При этом считается, что предельное состояние конструкции достигается при пропорциональном нагружении и полностью подобно рабочему состоянию.
При таком подходе нет надобности изучать предельного состояние и определять его параметры. Вместо этого достаточно определить напряжения в рабочем состоянии конструкции и найти их отношения к предельной величине напряжения для материала конструкции (предел прочности или предел текучести). Предельная величина напряжений конструкционного материала пред определяется опытным путем и при делении на коэффи-
циент запаса прочности для материала k дает так называемое допускаемое напряжение
предk
Следовательно, дальнейший расчет сводится к сравнению наибольшего рабочего напряжения конструкции с допускаемым напряжением конструкционного материала
max |
(13.1) |
По этой причине расчет по рабочему состоянию принято называть расчетом по допускаемым напряжениям.
Нагрузка на конструкцию, при которой условие (13.1) становится равенством, считается допускаемой нагрузкой, а несущей способностью считается та нагрузка, для которой будет выполняться условие
max пред
К недостаткам метода допускаемых напряжений следует отнести следующие моменты. Во-первых, он основан на допущении об идеальноупругих свойствах строительных материалов и игнорировании их пластических свойств. Во-вторых, допускаемые напряжения, составляющие некоторую долю предельного напряжения конструкционного материала, имеют смысл только при соблюдении пропорциональности между действующей нагрузкой и нагружением вплоть до разрушения, чего практически не бывает. И, наконец, используемый коэффициент запаса прочности не учитывал все факторы, влияющие на прочность конструкции.
129
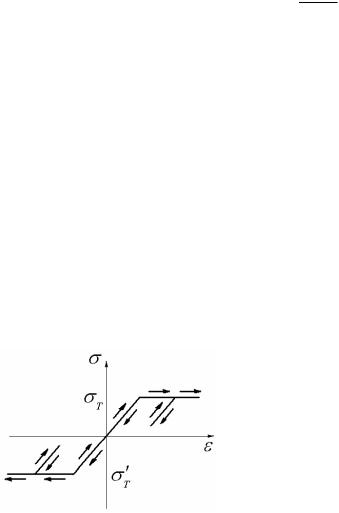
Второй подход определения несущей способности основан на рассмотрении предельного состояния конструкции, которое достигается в уп- руго-пластической стадии работы. Считается, что исчерпание несущей способности конструкции происходит при выключении из работы наиболее слабых мест и превращении ее в геометрически изменяемую систему, которая не может воспринимать дальнейший рост нагрузки.
Наименьшая нагрузка Pпред, при которой впервые произойдет пре-
вращение конструкции в геометрически изменяемую систему, и считается ее несущей способностью. Поэтому для ее определения рассматривается предельное состояние равновесия конструкции, непосредственно предшествующее ее превращению в геометрически изменяемую систему. Допускаемая нагрузка на сооружение имеет вид
P |
Pпред |
(13.2) |
|
K |
|
Здесь K коэффициент запаса прочности для конструкции в целом.
Такой метод определения несущей способности конструкции назы-
вается методом расчета по разрушающим нагрузкам или методом пре-
дельного равновесия. Определение несущей способности этим методом имеет две разновидности: статический и кинематический способы.
Статический способ состоит в отыскании наибольшей нагрузки, при которой в конструкции выключились из работы наиболее слабые места, но еще соблюдаются условия равновесия.
Кинематический способ основан на рассмотрении кинематически возможных состояний конструкции и отыскании наименьшей нагрузки, при которой конструкция превращается в геометрически изменяемую систему.
Основным отличием методом расчета по разрушающим нагрузкам по сравнению с методом расчета по допускаемым напряжениям является учет неупругих деформаций конструкционного материала. Следовательно, конструкция рассматривается как физически нелинейная
система.
При расчете методом разрушающих нагрузок материал конструкции считается идеальным упруго-пластическим и его поведение
Рис. 13.1 |
описывается диаграммой Прандтля (рис. 13.1). |
|||
На рис. 13.1 |
Т |
– предел текучести при |
||
|
||||
растяжении, Т – предел текучести при сжатии. Как показывают опыты, использование такой диаграммы не приводит к большим погрешностям,
130
