
книги / Теория механизмов и механика систем машин
..pdfДифференцируем (3.15):
li sin i i S1UDx SUDx1 X D |
|
1 X B |
1, |
(3.20) |
0 |
0 |
|
||
|
|
|||
li cos i i S1UDy SUDy1 YD |
1 YB 1. |
|
||
0 |
|
0 |
|
|
Получена система двух уравнений с двумя неизвестными ωi, S1. Коэффициенты и свободные члены системы:
|
|
a11 li sin i ; |
a12 UDx ; |
|
|
|
a21 li cos i ; |
a22 UDy ; |
(3.21) |
b1 |
X D |
1 X B 1 SUDx1; |
b2 YD 1 YB 1 SUDy1. |
|
|
0 |
0 |
0 |
0 |
Решая систему, получим угловую скорость ωi и относительную скорость S1.
3.2.6. Решение задачи об ускорениях группы 22
Исходные данные:
а) переменные (вход) – вторая строка таблицы 3.3; б) постоянные – те же.
Дифференцируем (3.20):
l |
cos 2 |
l sin |
i |
S2U |
Dx |
2S1U |
Dx |
1 SU |
Dx |
2 X |
D |
2 X |
|
B |
2 |
, |
|||||||||
i |
|
i i |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
l |
sin 2 |
l cos |
i |
S2U |
Dy |
2S1U |
Dy |
1 SU |
Dy |
2 Y |
2 Y |
|
2 . |
(3.22) |
|||||||||||
|
i |
i i |
i |
i |
|
|
|
|
|
|
|
|
D |
B |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
Снова получим систему двух уравнений с двумя неизвестными i , S2.
Коэффициенты системы остались прежними (3.21), свободные члены изменились и имеют вид:
b1 X D0 2 X B0 2 li cos i i2 2S1UDx1 SUDx 2, b2 YD0 2 YB0 2 li sin i i2 2S1UDy1 SUDy 2 .
Решая систему, получим угловое ускорение i и относительное ускорение S2.
3.3. Кинематика начального звена
Рассмотрим два типа начальных звеньев. Звеном первого типа будем задавать вход во вращательную кинематическую пару какой-либо группы, а звеном второго типа – в поступательную пару. При вращении начальных
41
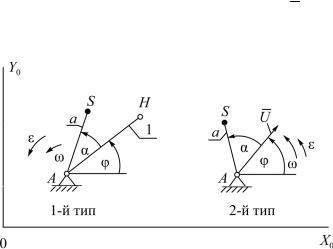
звеньев будем получать выходные параметры, к которым отнесем координаты точки Н звена, первые и вторые производные от этих координат для звена первого типа и проекции единичного вектора U , их первые и вторые производные для звена второго типа (рис. 3.2).
Рис. 3.2. Начальные звенья
Решение задач кинематики начального звена
С учетом исходных данных найдем координаты точки Н:
X H X A l cos ; |
YH YA l sin . |
(3.23) |
||
Проекции скорости точки Н: |
|
|
|
|
X H 1 l sin ; |
YH 1 l cos . |
(3.24) |
||
Проекции ускорения: |
|
|
|
|
X H 2 lcos ω2 |
l sin ; |
(3.25) |
||
Y 2 l sin 2 |
l cos . |
|||
|
||||
H |
|
|
|
|
3.4.Определение координаты, проекций скоростей
иускорений центров масс звеньев
Положения центров масс звеньев группы задаем отрезками аi,аk и углами i , k (см. рис. 3.1).
Пусть требуется определить перечисленные параметры для звена i группы 21 или группы 22. Проекции отрезка аi на оси X0 Y0:
aiX = ai sin i cos i sin i sin i , |
(3.26) |
aiY = ai sin i cos i cos i sin i . |
|
42
|
Координаты точки Si: |
|
|
|
|
X Si |
X B + aiX , |
(3.27) |
|
|
|
|
0 |
|
|
YSi |
YB |
+ aiY . |
|
|
|
0 |
|
|
|
Проекции скорости точки Si: |
|
|
|
|
X Si1 X B |
1+ aiX 1, |
(3.28) |
|
|
|
0 |
|
|
|
YSi1 YB 1+ aiY 1, |
|
||
|
|
0 |
|
|
где |
aiX 1= aiY i , |
aiY 1= aiX i . |
(3.29) |
|
|
Проекции ускорения точки Si: |
|
|
|
|
X Si 2 X B |
2 + aiX 2 , |
(3.30) |
|
|
|
0 |
|
|
|
YSi 2 YB 2 + aiY 2 , |
|
||
|
|
0 |
|
|
где |
aiX 2 = aiY 1 i aiY i ; |
aiY 2 = aiX 1 i + aiX i . |
(3.31) |
|
Пусть требуется определить проекции ускорения точки Sk. Найдем координаты точки Sk:
где
где
X Sk = X D +SD UDx + aKх , |
(3.32) |
|||||||
|
0 |
|
|
|
|
|
|
|
YSk =YD + SD U |
DY |
+ aKY , |
|
|||||
|
0 |
|
|
|
|
|
|
|
aKх = aK UDX cos k UDY sin k ; |
|
|||||||
aKY = aK UDY cos k UDX sin k . |
(3.33) |
|||||||
Проекции скорости точки Sk: |
|
|
|
|
|
|
|
|
XSk1= X D 1+SD 1 UDx + SD U |
Dx |
1 + aKх1, |
(3.34) |
|||||
0 |
|
|
|
|
|
|
||
YSk1=YD 1+ SD |
1 UDY + SD U |
DY |
1 + aKY 1, |
|
||||
0 |
|
|
|
|
|
|
||
aKX 1= aKY |
K ; aKY 1= aKX K . |
(3.35) |
||||||
Угловая скорость оси внешней поступательной кинематической пары D:
K UDX UDY 1 UDY UDX 1. |
(3.36) |
Эта скорость должна быть задана или предварительно вычислена. Проекции ускорения точки Sk:
43
X Sk 2 = X D |
2 +SD 2 UDx +2 SD 1 U |
Dx |
1 + SD U |
Dx |
2 + aKх 2 , |
(3.37) |
||||
0 |
|
|
|
|
|
|
||||
YSk 2 =YD 2 + SD 2 UDY +2 SD 1 U |
DY |
1+ SD U |
DY |
2 + aKY 2, |
|
|||||
0 |
|
|
|
|
|
|
||||
где |
aKX 2 = aKY 1 K aKY К , |
|
|
|
|
(3.38) |
||||
|
aKY 2= aKX 1 K aKX K . |
|
|
|
|
|
||||
Угловое ускорение εK находится дифференцированием (3.36): |
|
|||||||||
|
εK =UDK UDY 2 UDY UDX 2 , |
|
|
|
|
(3.39) |
||||
и должно быть задано или предварительно вычислено. |
|
|
|
|||||||
3.5. Функция положения и ее производные
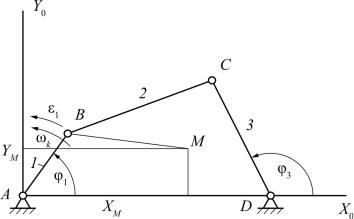
Рассмотрим рис. 3.3, на котором изображен механизм шарнирного четырехзвенника, состоящий из начального звена 1, структурной группы второго класса первого вида BCD и стойки 4. Обобщенной координатой механизма является угол i . Различают функцию положения звена и функцию
положения точки. Функцией положения звена называется зависимость вида3 3 1 , заданная аналитически, графически или в табличной форме.
Функцию положения точки представим в проекциях на оси координат:
X М XM 1 ; |
YM YM 1 . |
(3.40) |
Рис. 3.3. К определению понятия функции положения точки и звена
Дважды продифференцируем функцию положения звена по времени. Поскольку сама обобщенная координата является функцией времени,
то получим:
44
|
|
d |
; |
|
|
|
d 2 |
2 |
|
d |
. |
(3.41) |
3 |
|
3 |
|
3 |
||||||||
3 |
|
d |
1 |
|
3 |
|
d 2 |
1 |
|
d |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
Производная от функции положения звена по обобщенной координате называется первой передаточной функцией, или аналогом угловой скорости (безразмерная величина). Вторая производная от функций положений по обобщенной координате называется второй передаточной функцией, или аналогом углового ускорения (безразмерная величина). В (3.38) i и i –
обобщенные угловая скорость и угловое ускорение. Продифференцируем функцию положения точки:
X M 1 dX M 1 ; d 1
YM 1 dYM 1 ; d 1
X |
M |
d 2 X M 2 |
dX M |
; |
(3.42) |
|||
|
d 2 |
|
1 |
d |
1 |
|
||
|
|
1 |
|
|
|
1 |
|
|
Y d 2YM |
2 |
dYM |
. |
|
||||
M |
d 2 |
1 |
|
d |
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
В (3.42) первые и вторые производные от координат точки по обобщенной координате называются проекциями аналогов скоростей и ускорений точки (в системе СИ размерность в метрах). Если принять обобщенную1 1 (безразмерная величина) и 1 0, то из выражений (3.41) и (3.42)
видно, что истинные скорости и ускорения будут совпадать с их аналогами.
3.6. Кинематический анализ манипулятора
Прямая задача о положении манипуляторов позволяет определить координаты схвата или его траекторию движения, а также ориентацию схвата вдоль всей траектории. Прямая задача о скоростях состоит в определении абсолютных линейных скоростей точек звеньев манипулятора и угловых скоростей звеньев при заданных законах изменения обобщенных координат. Для кинематического исследования пространственных кинематических цепей существуют различные методы. При исследовании кинематики роботов рациональнее использовать матричный метод.
Рассмотрим манипулятор с тремя степенями свободы. Функцией положения точки D схвата (рис. 3.4) будет зависимость ее радиуса-вектора ρ(0)D от
обобщенных координат и постоянных длин звеньев lВС и lDC. Данный механизм с незамкнутой кинематической цепью является статически определимым, без избыточных связей (q = 0), поскольку он собирается без натягов. В механизме три одноподвижные пары: две из них вращательные (А, С) и одна поступательная (В). Обобщенных координат три: 10 – угол поворота
45
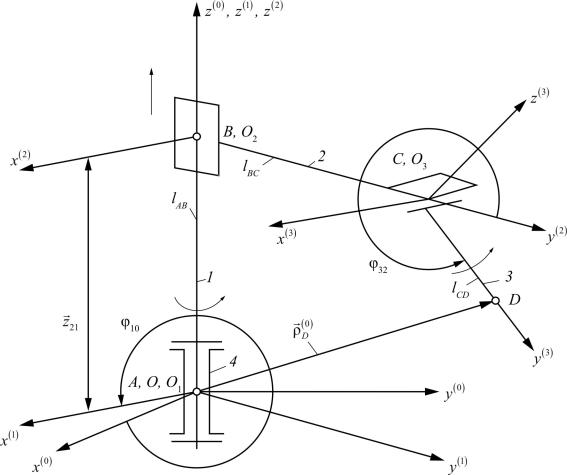
звена 1 относительно стойки 4; z21 – линейное перемещение звена 2 относительно звена 1; 32 – угол поворота звена 3 относительно звена 2. Число степеней свободы W = 3 подтверждается и по формуле Малышева:
5 |
|
6 3 5 3 3. |
W 6n (6 i) pi q |
||
i 1 |
|
|
Рис. 3.4. Кинематический анализ манипулятора
Система координат O1x(1) y(1) z(1) связана со звеном 1, вращающимся вокруг оси z(1), система O2x(2) y(2) z(2) – со звеном 2, движущимся прямолинейно
относительно звена 1, а система О3х(3) у(3) z3 – со звеном 3, вращающимся вокруг оси z (3). Оси x(1), x(2), x(3) параллельны.
Функция положения в матричной форме имеет такой вид:
ρ(0)D ρ(0)D (φ10 , z21, φ32 ),
ρ(0)D T10 , T21, T32 , ρ(3)D ,
46
где
|
x(0) |
|
|
|
|
|
cos φ |
|
–sin φ |
|
0 |
|
0 |
|
|
1 |
0 |
0 |
0 |
|
|
||
|
D |
|
|
|
|
|
|
10 |
10 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|||
(0) |
y(0) |
|
; |
T |
|
|
sin φ |
|
cos φ |
|
0 |
|
; |
T |
1 |
0 |
0 |
|
; |
||||
D |
|
|
|
10 |
10 |
|
|
|
|
|
|
|
z21 |
|
|||||||||
D |
zD(0) |
|
|
10 |
|
|
0 |
|
0 |
|
1 |
|
0 |
|
21 |
0 |
0 |
1 |
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 0 1 |
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|||||||
|
|
|
|
|
1 |
|
0 |
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
T |
|
0 |
|
cos φ |
|
–sin φ |
|
l |
|
|
|
(3) |
l |
|
|
|
|
|
|||
|
|
|
|
|
32 |
|
32 |
|
BC ; |
|
|
CD . |
|
|
|
|
|||||||
|
|
|
32 |
|
0 |
|
sin φ32 |
cos φ32 |
|
0 |
|
|
D |
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
0 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Последовательным умножением матрицы приводят к равенству
x(0) |
|
|
–l |
BC |
sin φ |
|
l |
|
|
sin φ cos |
φ |
32 |
|
|
||||||
|
D |
|
l |
|
|
10 |
|
CD |
|
10 |
|
|
|
|||||||
y(0) |
|
BC |
cos φ |
|
l |
|
cos φ cos |
|
|
|
, |
|||||||||
|
D |
|
|
|
|
10 |
|
CD |
|
|
10 |
32 |
|
|||||||
z(0) |
|
|
|
|
|
|
z |
21 |
|
l |
|
|
sin φ |
32 |
|
|
|
|
||
|
D |
|
|
|
|
|
|
|
|
CD |
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
следовательно, искомые координаты точки D в неподвижной системе Ох(0) y(0) z(0) будут следующими:
xD(0) –lBCsin 10 lCDsin 10cos 32 , yD(0) lBCcos 10 lCDcos 10cos 32 ,
zD(0) z21 lCDsin 32.
С помощью зависимостей, имея заданный диапазон изменения координат точки D, можно подобрать нужные значения длин звеньев lВС, lCD и диапазоны изменения обобщенных координат 10, z21 и 32.
Скорость движения схвата и отдельных звеньев манипулятора определяется не только характером рабочего процесса, но и условиями безопасности для обслуживающего персонала. Если зависимости обобщенных координат от времени известны, то скорости можно найти дифференцированием по времени функции положения. Например, для рассмотренного манипулятора с тремя степенями свободы при заданных зависимостях 10(t), z21(t) и 32(t) проекции вектора скорости точки D схвата на оси координат получим, дифференцируя выражения:
47

V |
x |
(0) |
–ω cos φ (l |
BC |
l |
|
cos φ |
32 |
) ω l |
|
sin φ |
sin φ |
32 |
, |
|||||||
Dõ |
|
D |
1 |
10 |
CD |
|
|
|
32 CD |
10 |
|
|
|
||||||||
V |
y(0) |
–ωsin φ (l |
BC |
l |
|
cos φ |
32 |
|
) ω |
|
l |
|
cos φ sin φ |
32 |
, |
||||||
Dy |
|
D |
1 |
10 |
CD |
|
|
|
|
32 CD |
10 |
|
|
|
|||||||
|
|
|
V |
z(0) V |
ω |
l |
|
|
cos φ |
32 |
. |
|
|
|
|
|
|
||||
|
|
|
Dz |
D |
|
21 |
|
|
32 CD |
|
|
|
|
|
|
|
|
|
|||
Величину и направление вектора скорости точки D найдем по формулам:
V |
V 2 |
V 2 |
V 2 |
, cos α VDx , |
|||
D |
Dx |
|
Dy |
|
Dz |
|
VD |
|
|
|
|
|
|
|
|
|
cos β |
VDy |
|
, cos γ |
V |
||
|
|
|
Dz . |
||||
|
V |
|
|||||
|
|
|
|
|
|
V |
|
|
|
|
D |
|
|
|
D |
где , , – направляющие углы вектора скорости.
3.7. Графоаналитический метод кинематического исследования рычажных механизмов
Графоаналитический метод, или метод планов, основан на элементах векторной алгебры. При кинематическом исследовании составляются векторные уравнения для скоростей или ускорений механизма в данном положении. Полученные уравнения решаются графически в порядке присоединения структурных групп к ведущему звену и к стойке. Метод планов применяют тогда, когда имеется схема механизма в данном положении. Рассмотрим примеры применения графоаналитического метода.
Определение предельных положений механизма (графический метод)
Решение задачи начинают с определения предельных положений механизма, когда рабочий орган механизма занимает крайнее положение. Рассмотрим способы, пользуясь которыми можно в зависимости от типа механизма найти предельные положения.
Для шарнирного четырёхзвенника (рис. 3.5, а, б) предельные положения коромысла 3 будут тогда, когда кривошип 1 и шатун 2 располагаются на одной прямой. Из точки А в масштабе радиуса кривошипа, а из точки D радиусом коромысла проводим окружности. Затем из А проводим засечки длинами АВ+ВС и ВС–АВ до пересечения с траекторией коромысла в точках С1 и С2. Полученные точки С1 и С2 соединяем с точкой А отрезками, пересекающими окружность кривошипа в точках В1 и В2. Положения механизма, соответствующие схемам AB1C1D и AB2C2D, – предельные
(рис. 3.5, б).
48
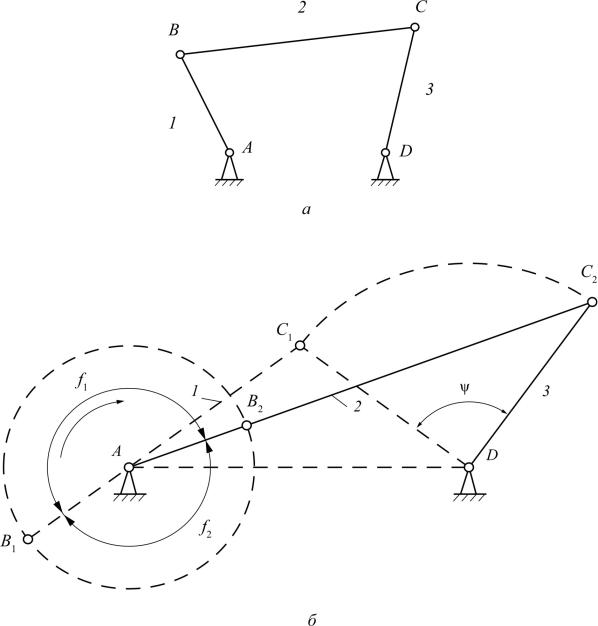
Pис. 3.5. Шарнирный четырехзвенник: à — кинематическая схема; á — крайние положения
Методика определения крайних положений для кривошипно-пол- зунного механизма (рис. 3.6) аналогична той, которая рассмотрена выше.
Для механизма с качающейся кулисой определение предельных положений начинают с построения окружности кривошипа 1 с центром в точке А. Затем проводятся две касательные к этой окружности из точки D – центра качения кулисы 3. Эти прямые и характеризуют схемы AB1D и AB2D механизма, соответствующие двум крайним положениям (рис. 3.7).
49
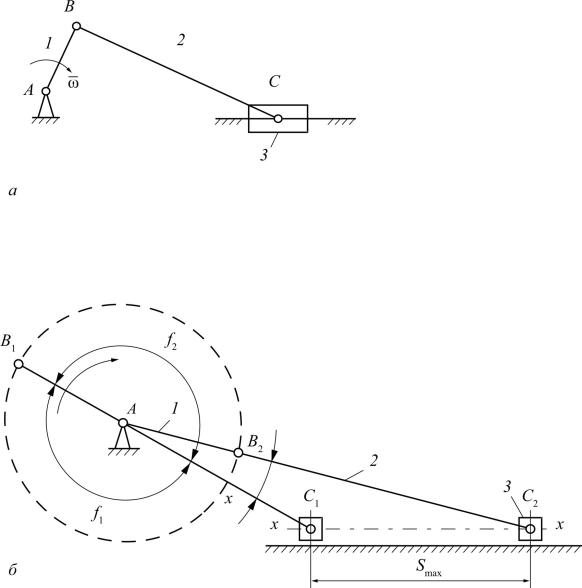
Рис. 3.6. Кривошипно-ползунный механизм:
à — кинематическая схема; á — крайние положения
50
