
книги / Строительная механика, динамика и устойчивость композитных конструкций
..pdfВарьируем на возможных перемещениях iT
A1i k i i t |
(5.1.21) |
или |
|
n |
|
A1 A1i K , |
(5.1.22) |
i 1 |
|
где [K] глобальная матрица жесткости, |
вектор узловых пере- |
мещений; аналогично |
|
A2 T F , |
(5.1.23) |
A2 F , |
(5.1.24) |
где F вектор узловых нагрузок. Так как |
U 0 есть условие |
экстремума функционала, следовательно, приходим к основной разрешающей системе линейных алгебраических уравнений
K F F |
(5.1.25) |
– уравнения удовлетворяют геометрическим, физическим соотношениям и граничным условиям в усилиях, и, так как функционал U эквивалентен уравнениям равновесия, следовательно, удовлетворяются и уравнения равновесия.
6. Граничные условия в перемещениях. Пусть перемещения,
например, в i-м узле заданы из граничных условий i * , тогда
количество уравнений в разрешающей системе на одно меньше, поэтому необходимо модифицировать правую часть
|
F F K *, |
(5.1.26) |
где F |
есть i-я строка матрицы K , после чего следует удалить |
|
i-e уравнение в системе. Практически поступают следующим образом: полагают равными нулю компоненты F , F Т и используют равенства
181
Kii 1, |
(5.1.27) |
Ff *, |
(5.1.28) |
Таким образом, из решения системы линейных уравнений получимузловые перемещения и далееопределимдеформации
B i |
(5.1.29) |
и напряжения |
|
C |
(5.1.30) |
в каждом элементе пластины. Переходя к напряжениям в слоях материала пластины и используя соответствующий критерий прочности, можно провести прочностной анализ и сделать выводы о начале разрушения конструкции. На основе соотношения
|
|
|
|
|
|
|
u |
|
|
N |
|
i |
(5.1.31) |
v |
|
|
|
|
|
|
можно определить перемещения в любой точке пластины и провести анализ жесткости пластины.
5.2.Расчет стержневых конструкций
исетчатых панелей
Элементы стержневых конструкций (рис. 5.5, а) это стержни из однонаправленного волокнистого композиционного материала. Сетчатая панель (рис. 5.5, б) используется или независимо в качестве конструкции, или как внутренний сэндвичевый слой слоистого композита.
Рассмотрим типичный балочный элемент в локальной системе координат (рис. 5.6) – системе, связанной с конечным элементом. Координатная ось х направлена вдоль стержневого конечного элемента, координаты узлов: Xi 0, Xi L, где L длина эле-
мента. Вектор обобщенных перемещений
182
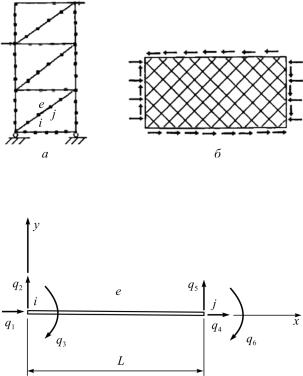
q T q1 ,q2 , q3 , q4 ,q5 ,q6 , |
(5.2.1) |
где q1,q2 и q4 , q5 компоненты смещений соответственно i-го и j-го узлов конечного элемента, q3 , q6 углы поворота соответствующих узловых сечений.
Рис. 5.5. Примеры стержневой конструкции (а) и сетчатой панели (б)
Рис. 5.6. Конечный элемент в локальной системе координат
Деформация элемента характеризуется продольным смещением и(х) и поперечным прогибом w(x).
При этом продольное смещение и(х) обусловлено продольной деформацией и связано с узловыми перемещениями q1,q4 ,
а поперечное смещение w(x) зависит от q2 ,q3 ,q5 ,q6 .
183
Аппроксимируем и(х) линейной функцией |
|
||||||||||||
|
u x a1 |
a2 x, |
|
|
|
(5.2.2) |
|||||||
где константы 1, 2 определяем из условий |
|
||||||||||||
|
u 0 q |
|
a |
|
|
|
|
||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
(5.2.3) |
||
u L q |
a a L; |
|
|||||||||||
|
|
|
4 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 q1, |
|
|
|
|
(5.2.4) |
||||||
|
a2 q4 |
q1 |
|
|
|
(5.2.5) |
|||||||
|
|
|
|
L |
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
u x q1 |
x L |
|
q4 |
x |
|
, |
(5.2.6) |
||||||
|
L |
|
|
|
L |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
где базисные функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x L |
, |
|
x |
. |
|
|
|
|
(5.2.7) |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
L |
|
|
L |
|
|
|
|
|
|||
Для аппроксимации прогиба w(x) для балочного конечного элемента воспользуемся степенным полиномом
w x c1 c2 x c3 x2 c4 x3
и константы с1, ,с4 определим из условий
w 0 q2 c1 |
|
|
|
|
2 |
3 |
|
w L q5 |
c1 c2 L c3 L |
c4 L |
. |
|
c2 |
|
|
w 0 q3 |
|
|
|
|
|
2 |
|
w L q6 |
c2 2c3 L 3c4 L |
|
|
(5.2.8)
(5.2.9)
184
Окончательно получим
w x q23 |
2x3 3Lx2 L3 |
q53 2x3 |
3Lx2 |
|
|||||
|
L |
|
|
L |
|
|
(5.2.10) |
||
|
q4 |
|
x3 2Lx L2 x |
q6 |
x3 |
Lx2 . |
|||
|
|
|
|||||||
2 |
2 |
|
|||||||
|
L |
|
|
L |
|
|
|
||
Упругая энергия деформирования стержневого конечного элемента Ae A1 A2 может быть представлена суммой линейной деформации
|
|
|
A1 |
1 |
L |
du 2 |
|
|
|
|
|
(5.2.11) |
||||
|
|
|
|
SE |
dx |
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
0 |
dx |
|
|
|
|
|
|
||
и изгибной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
1 |
L |
d 2W 2 |
dx, |
|
|
|
(5.2.12) |
||||
|
|
|
2 |
EI |
|
dx |
2 |
|
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
1 |
L |
du 2 |
|
1 |
L |
d 2W 2 |
(5.2.13) |
|||||||
A |
|
SE |
|
|
dx |
|
EI |
|
|
2 |
|
dx, |
||||
|
|
2 |
0 |
dx |
|
|
2 |
0 |
|
dx |
|
|
|
|
||
где Е модуль Юнга стержня вдоль оси, S и I – площадь и момент инерции поперечного сечения стержня. Подставим аппроксимации u(x) и w(x) в выражение для энергии упругого деформирования
|
e |
|
1 |
L |
q1 |
|
|
q4 |
2 |
1 |
L |
2 |
q2 |
12x 6L |
|||||
A |
|
|
|
SE |
|
|
|
dx |
|
EI |
|
|
|
||||||
|
2 |
L |
L |
2 |
3 |
||||||||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
L |
|
(5.2.14) |
||||||
|
q5 |
|
|
|
|
|
|
q3 |
|
|
|
|
q6 |
|
|
|
2 |
||
|
|
3 |
12x 6L |
|
|
16x 4L |
|
|
|
6x |
2L dx |
||||||||
|
|
2 |
|
2 |
|
||||||||||||||
|
L |
|
|
|
|
|
|
L |
|
|
|
|
L |
|
|
|
|
||
или после интегрирования получим
A |
e |
|
1 |
T |
e |
q , |
(5.2.15) |
|
2 |
q k |
|
||||
|
|
|
|
|
|
|
185
где
|
|
|
SL2 |
0 |
0 |
SL2 |
0 |
0 |
|
|
|
|
|
|
|
12I |
6IL |
0 |
12I |
6I |
|
|
|
|
|
|
|
|
|
|
|||||
k |
E |
|
4IL2 |
0 |
6I |
2IL2 |
, |
(5.2.16) |
|||
|
|
|
|
|
|
|
|
|
|||
l |
3 |
|
|
2 |
0 |
0 |
|||||
|
|
|
|
|
SL |
|
|
|
|||
|
|
|
|
sim. |
|
|
12I |
6IL |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4IL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
после варьирования по переменным q
|
|
|
e |
|
e |
q , |
(5.2.17) |
|
|
|
A |
k |
|
||
следовательно, |
ke |
локальная матрица жесткости стержневого |
|||||
|
|
|
|
|
|
|
|
элемента.
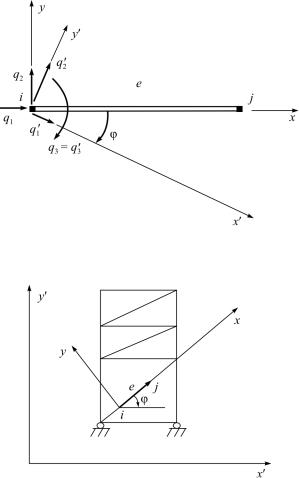
Построение глобальной матрицы жесткости не может быть выполнено путем формального суммирования локальных матриц жесткости элементов, так как локальные матрицы построены для локальной системы координат x, y (рис. 5.7), связанной с эле-
ментом, а обобщенные узловые перемещения конструкции исследуются в глобальной или конструктивной системе координат
x , y (рис. 5.8). Соотношения между координатами вектора q в этих двух системах координат, например, для i-го узла:
|
q |
q cos q sin |
|
|
|
1 |
1 |
2 |
|
q |
q sin q cos |
(5.2.18) |
||
|
2 |
1 |
2 |
|
|
|
q |
q |
|
|
|
|
||
|
1 |
3 |
|
|
|
|
|
|
|
и аналогично для второго j-го узла. Таким образом, |
|
|||
|
|
|
q , |
(5.2.19) |
|
|
q |
||
где матрица поворота или матрица вращений:
186
cos |
sin |
0 |
0 |
0 |
0 |
|
|
|
|
cos |
0 |
0 |
0 |
|
|
sin |
0 |
|
|||||
|
0 |
0 |
1 |
0 |
0 |
0 |
(5.2.20) |
|
0 |
0 |
0 |
cos |
sin |
. |
|
|
0 |
|
|||||
|
0 |
0 |
0 |
sin |
cos |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
Рис. 5.7. Узловые усилия конечного элемента в локальной и глобальной системах координат
Рис. 5.8. Локальная и глобальная системы координат
187
Запишем упругую энергию деформированию стержневого
элемента в глобальной системе координат |
|
|
|
в виде |
|
|||||||||||
x , y |
|
|
||||||||||||||
A |
e |
|
1 |
T |
e |
|
1 |
|
T |
T |
e |
|
(5.2.21) |
|||
|
2 |
q k |
|
q |
2 |
q |
|
|
k |
|
q , |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
для вариаций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
T |
|
|
e |
|
|
|
|
|
(5.2.22) |
|
|
|
|
|
A |
|
k |
|
q |
; |
|
|
|
||||
таким образом, матрица жесткости элемента в глобальной системе координат
ke |
T ke |
. |
(5.2.23) |
||
|
|
|
|
|
|
Далее формирование глобальной матрицы жесткости [K] проводим обычным для метода конечных элементов образом; система линейных алгебраических уравнений имеет вид
K F , |
(5.2.24) |
где [K] – квадратная матрица размером 3n, n – число узлов в стержневой конструкции; {δ} – вектор обобщенных перемещений; {F} – вектор обобщенных нагрузок
Fx1
F Fy1 (5.2.25)
M1...
Рис. 5.9. Распределение напряжений от растяжения (а) и изгиба (б) по сечению конечного элемента
188
Напряжения в стержневых элементах можно представить через сумму напряжений, возникающих от растяжения (рис. 5.9, а)
a E E du E q4 q1 dx L
и от изгиба (рис. 5.9, б)
|
|
|
|
|
|
b |
Ez |
d 2 w |
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Ez |
q |
2 |
12x L |
q |
12x 6L q |
|
6x 4L |
q |
2 |
|||
|
|
3 |
5 |
|
|
3 |
3 |
2 |
|
|||
|
|
|
L |
|
|
|
L |
|
|
L |
|
|
(5.2.26)
6x L |
(5.2.27) |
||
, |
|||
2 |
|
||
L |
|
|
|
где компоненты q в локальной системе координат находим через определяемые из решения системы линейных алгебраических уравнений компоненты q по формуле
|
1 |
|
(5.2.28) |
|
q |
q . |
|
|
Типичные граничные условия в перемещениях: |
q1 0 или |
|
q2 |
0 для подвижного шарнира соответственно вдоль оси z или |
||
х; |
q1 q2 0 Для неподвижного шарнира или q1 q2 |
q3 0 для |
|
жесткой заделки; процедура учета граничных условий в системе линейных алгебраических уравнений традиционна.
5.3. Изгиб пластин
Рассмотрим пластину, характерные размеры которой связаны неравенствами:
t a,t b, |
(5.3.1) |
под действием поперечных нагрузок и изгибных моментов
(рис. 5.10).
Деформирование пластины полностью характеризуется прогибом w(x,y). Дискретизация пластины прямоугольными элемен-
тами (рис. 5.11).
189
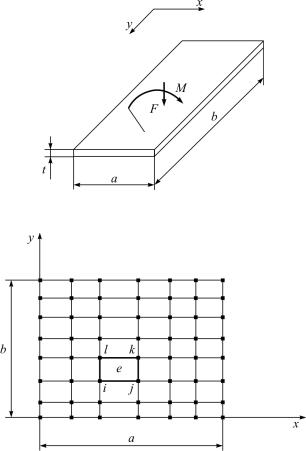
Рис. 5.10. Пластина под нагрузкой
Рис. 5.11. Дискретизация пластины
Рассмотрим элемент e (рис. 5.12) с вершинами i, j, k, l. Коор-
динаты i-й вершины ( Xi ,Yi ).
Аппроксимация прогиба в пределах элемента. Прогиб эле-
мента w выразим через прогибы узлов wi , wj , wk , wl и углы поворота xi , yi , xj , yj , …– всего через 12 параметров; введем обозначение
190
