книги / Строительная механика, динамика и устойчивость композитных конструкций

совпадающие с естественными граничными условиями для уравнения Остроградского – Эйлера в вариационном подходе. Дополняя полученную систему уравнений начальными условиями

приходим к точно такой же постановке краевой задачи динамики упругих конструкций, что и для вариационного подхода.

Полученные в разделах 1.2.1 и 1.2.2 постановки краевых задач динамики позволяют исследовать поведение плоских и пространственных тел при действии нестационарных нагрузок. В прикладных расчетах часто приходится проводить анализ стержневых и тонкостенных элементов конструкций, рассмотрим особенности получения определяющих соотношений динамики и для этих практически важных случаев.

1.2.3. Продольные колебания стержней

Стержень – одномерное упругое тело. Пусть ось Х – ось стержня, l – длина. Стержень совершает продольные колебания, тогда перемещения точек, лежащих в плоскости одного перпендикулярного оси стержня сечения, являются одинаковыми. Получим уравнение движения, используя вариационный принцип Гамильтона:

где E – модуль Юнга, F – площадь поперечного сечения.

где q – продольная распределенная нагрузка, N – нагрузка на торцах стержня. Используя уравнение Остроградского – Эйлера, получаем уравнение движения

21

известное в математической физике как волновое уравнение. Типичные граничные условия для задачи продольных коле-

баний стержня:

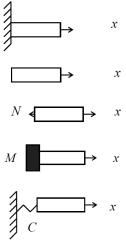
5.на конце упругое закреп- EF u Cu*) . ление x

1.2.4. Крутильные колебания стержней

Принимаем гипотезу плоских сечений стержня при кручении, пусть (x,t) – угол закручивания. Получим уравнение движения,

используя вариационный принцип Гамильтона

где G – модуль сдвига; J0 – полярный момент инерции

где – распределенный крутящий момент; M – крутящий момент на концах стержня. Используя уравнение Остроградского – Эй-

22

лера, получаем волновое уравнение, описывающее процесс крутильных колебаний стержня

1.2.5. Изгибные колебания стержней

Примем гипотезу плоских сечений, перпендикулярных изогнутой оси стержня. Получим уравнение движения, используя вариационный принцип Гамильтона

где w – прогиб стержня, перемещение перпендикулярное оси x; J – осевой момент инерции сечения стержня

где q – поперечная распределенная нагрузка по длине стержня; Q – перерезывающее усилие на боковых гранях. Используя урав-

23

нение Остроградского – Эйлера, получим уравнение изгибных колебаний стержня

По сравнению с продольными и крутильными колебаниями увеличивается порядок частных производных по х, следовательно, необходимо большее число граничных условий.

Типичные граничные условия в задаче изгибных колебаний стержней:

1.2.6. Колебания криволинейных стержней

Введем следующие обозначения: S – криволинейная ось

стержня; R(S) – радиус кривизны; max r 1; u(S) – перемеще-

R

ние вдоль оси S стержня; w(S) – перемещение поперек оси стрежня. Тогда выражения для составляющих полной энергии системы будут иметь вид

24

Так как динамическое поведение стержня характеризуется функциями U(S) и w(S), получим систему двух уравнений Остроградского – Эйлера

Граничные условия принимаются такие же, как в случае изгиба стержня, но вместо x надо принять S.

1.2.7. Изгибные колебания пластин

Пластина – тело, у которого один из размеров (толщина) много меньше двух других размеров и координатная поверхность которого – плоскость. Динамическое поведение рассмотрим в рамках технической теории изгиба анизотропных пластин (модель Кирхгофа – Лява). Согласно данной модели:

–деформация пластины определяется только прогибом;

–нормаль к срединной поверхности после деформирования остается нормальной, прямолинейной и сохраняет свою длину;

–срединная поверхность не деформируется;

–прогибы пластин малы.

Энергия деформирования определяется следующим образом:

25

где – площадь пластины; M x , M y – изгибающие моменты; M xy – крутящий момент; x , y , xy , – обобщенные изгибные де-

формации (кривизны).

Для ортотропной пластины упругие соотношения:

Исключая момент из выражения энергии деформирования, получим

Прогибы пластин малы, следовательно, кривизны пропорциональны вторым частным производным прогиба по пространственным координатам

26

Кинетическая энергия (без учета вращений)

Потенциал внешних усилий (распределенная нагрузка по поверхности q(x,y,t))

и составляя уравнения Остроградского – Эйлера для функционала, получим

D* D12 2D66 .

Получили уравнение движения ортотропной пластины при изгибе. Условия на контуре (по два условия):

–жесткая заделка;

–шарнир;

–начальные условия;

1.2.8. Динамическое поведение оболочек

Ограничимся анализом осесимметричных оболочек; вектор перемещений в этом случае описывается двумя компонентами: u – смещение точек срединной поверхности вдоль образующей S; w – смещение точек срединной поверхности вдоль нормали n (рис. 1.7). В оболочке действуют изгибающие моменты Ms и M

и усилия в срединной поверхности Ns и N .

От действия изгибающих моментов изменяется серединная поверхность, от усилий возникают продольные деформации.

27

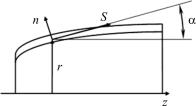
Рис. 1.7. Координатная система осесимметричной оболочки

где l – длина оболочки по меридиану. Упругие соотношения:

где для однородной ортотропной оболочки:

при этом Bij 0, если координатная поверхность является сре-

динной поверхностью.

Связь деформаций с перемещениями:

28

Подставляя геометрические и физические соотношения в вы-

Подставляя выражения для U, T, П в функционал и сопоставляя для него систему уравнений Остроградского – Эйлера, получаем уравнения движения тонкой анизотропной оболочки (получается система двух дифференциальных уравнений в частных производных относительно функций u(S,t) и w(S,t)).

Граничные и начальные условия формулируются традиционно и приводят к постановке краевой задачи динамики осесимметричной оболочки.

1.2.9. Свободные колебания упругих систем

Анализ полученных ранее уравнений движения упругих систем (плоских и объемных, стержневых и тонкостенных конструкций) показывает, что общая запись уравнений динамики может иметь вид

где А и С дифференциальные операторы, инерционный и упругий соответственно, u (r ,t) – поле перемещений, F (t) – внешняя нестационарная нагрузка.

29

В случае свободных колебаний упругих систем получается, что внешние нагрузки отсутствуют F(t) 0 . В этом случае необходимо исследоватьоднородное дифференциальноеуравнение вида:

Так как свободные колебания совершаются по гармоническому закону, то общее решение однородного дифференциального уравнения будем искать в виде:

Подставляя вид решения (1.67) в уравнение (1.66) получим

Значения параметра 2 , при которых уравнение (1.2.9.4) имеет решение, отличное от , называют собственными значениями ( , в свою очередь, называют собственными частотами). Функции , соответствующие собственным значениям 2 , называются собственными элементами уравнения (1.68), определяющими собственные формулы колебаний упругой системы. Совокупность собственных частот уравнения (1.2.9.4) называют спектром. Спектр собственных частот обычно упорядочивают в порядке возрастания 1 2 3 K, причем, 1 – первая (низшая) собственная частота. Собственным формам присваивают номера соответствующих частот, например 1 – первая форма свободных колебаний механической системы.

Собственные формы i определяют общее решение уравне-

где i = 1,2 K, ui – константы.

30